Распределение Ферми—Дирака

Хотя электроны в металле относительно свободны в своем движении, принцип запрета Паули приложим и к ним в той же мере, как к электронам,

движущимся по орбитам в атомах. Никакие два электрона внутри металла не могут занимать одно и то же энергетическое состояние. Частицы, которые подчиняются принципу запрета Паули, подпадают под действие ста­тистики Ферми—Дирака.

Пусть f(E) — вероятность того, что данное квантовое состояние занято электроном, тогда при нуле температур имеем:

f(E) = 1 при E< E_F

f(E) = 0 при E > E_F

При температуре, отличной от нуля, вероятность заполнения данного квантового состояния дается формулой распределения Ферми -Дирака:

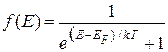(247)

В этой формуле Е - энергия рассматриваемого квантового состоя­ния, E_F — энергия Ферми (энергия самого высокого заполненного уровня), k - постоянная Больцмана, Т — абсолютная температура. На рисунке 85 показана функция распределения f(E) при абсолют­ном нуле температур и при двух более высоких температурах Т. Обратим внимание, что при Е = Е_F, f(E) = 1/2 при всех температурах.

При температуре Т = 0 К, f(Е) = 1 при Е < Е_F, так как все энерге­тические состояния заполнены до энергетического уровня Е = Е_F. Число электронов с энергиями меньшими или равными энергии Ферми, равно:

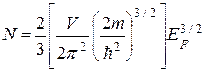(248)

При Т = 0 К, энергия ферми равна

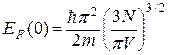(249)