Дифракция от одной щели

Рассмотрим дифракцию на одной щели в параллельных лучах. Пусть на узкую щель, проделанную в непрозрачном экране, падает нормально к экрану параллельный пучок света. Рассмотрим дифракционную картину вдали от экрана, теоретически - в бесконечности. рассмотрим свет, прошедший через щель под углом j. Оптическая разность хода между крайними лучами, идущими от щели в произвольном направлении D = a sinj. Пусть плоская волна падает пер­пендикулярно на экран, в котором имеется длинная узкая щель шири­ной а (рис.46). Когда фронт волны дойдет до щели и займет положение АВ, то все его точки явятся новыми источниками волн, распространяющихся во все стороны вперед от щели. Рассмотрим волны, распространяющиеся от точек плоскости АВ в направлении, составляющем некоторый угол j с первоначаль­ным направлением. При наблюдении их глазом, адаптированным на бесконеч­ность (или через трубу), соответствующие лучи после преломле­ния хрусталиком сойдутся в одну точку на сетчатке и будут ин­терферировать друг с другом. Можно также поставить линзу, параллельную плоскости АВ, и тогда, как показано на этом же рисунке, эти параллельные лучи после преломления сойдутся в некоторой точке М в фокальной плоскости линзы. Располагая в этой фокальной плоскости экран Е, можно на нем наблюдать результат интерференции для волн, распространяющихся от щели под различными произвольными углами j к первоначальному направлению. Разобьем волновую поверхность, вырезаемую щелью, на зоны Френеля, при этом разность хода между двумя пучками света от соседних зон будет равна l/2. Следовательно, при интерференции они должны гасить друг друга. Допустим, что угол j выбран таким образом, что на щели укладывается четное число зон Френеля. Свет от каждой зоны будет погашен светом соседней зоны, и под таким углом в бесконечности должен наблюдаться минимум. Условие минимума имеет вид:

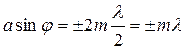, (163)

где m = 1, 2, 3, …

Если число зон Френеля, укладывающихся в отверстии нечетное, то наблюдается дифракционный максимум, соответствующий действию одной не скомпенсированной зоны Френеля.

Условие максимума имеет вид:

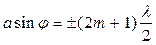(164)

Весь световой фронт, наблюдаемый под углом j = 0, принимается за одну зону, и, следовательно, в этом направлении наблюдается максимум. Он имеет самую большую интенсивность и называется главным максимумом. Распределение интенсивности на экране, получаемое при дифракции на щели приведено на рис.46. Дифракция выражена тем ярче, чем уже щель и чем больше длина волны.