Дифракция от многих щелей. Дифракционная решетка.

Рассмотрим несколько параллельных друг другу щелей одинаковой ширины а, расположенных на одинаковом расстоянии b, друг от друга. Величина а +b = d называется постоянной дифракционной решётки.

Пусть плоская монохроматическая волна падает нормально на поверхность решётки (рисунок 47). Линза собирает параллельные лучи, идущие под углом j к главной оптической оси, в одну и ту же точку В на экране, расположенном в фокальной плоскости линзы. Если число щелей N, то кроме дифракции от каждой щели наблюдается интерференция N пучков. Дифракционная картина на экране определяется как результат взаимной интерференции волн идущих от всех щелей.

На центральной линии экрана (проходящей через главный фокус линзы, лучи) лучи, идущие от всех щелей, сходятся без дополнительной разности хода, т.е. в одинаковой фазе. При этом их амплитуды просто складываются, и в случае N одинаковых щелей амплитуда результирующего колебания будет в N раз, а интенсивность в N² раз больше, чем от одной щели.

Лучи, идущие от разных щелей под углом j, сходятся в побочном фокусе линзы В, пройдя различные пути и имея различные фазы колебаний. Они будут давать при интерференции более сложную картину. Рассмотрим две соседние щели. Из рис.47 видно, что лучи, идущие от соответственных точек (М и С, N и D) обеих щелей, имеют одну и ту же разность хода:

D = (a+b)sinj = d sinj,

и приходят в точку М со сдвигом фаз:

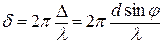(165)

Если в точке М амплитуды всех колебаний направлены одинаково, т.е. сдвиг фаз кратен 2π, то в ней будет наблюдаться максимум освещённости. Таким образом, условие максимума имеет вид:

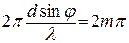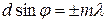или: (166)

Если же волны приходят в точку М в противофазах ( 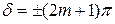), то они

гасят друг друга и наблюдается минимум интенсивности света. Таким образом, условие минимумапри дифракции на решётке имеет вид:

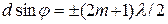(167)

В формулах (166) и (167) т = 0, 1, 2, 3, … - порядок соответственно максимума или минимума.

Следует отметить, что хотя положение главных максимумов при дифракции на решётке не зависит от числа щелей, наличие большого числа щелей очень существенно:

1) яркость каждого максимума растёт согласно А²= N²А₁²;

2) ширина каждой линии убывает согласно 1/N.

Таким образом, при увеличении числа щелей возрастает точность определения положения линии, соответствующей максимуму интенсивности, что важно при дифракционном спектральном анализе.

Если на решётку падает белый свет, то дифракционные максимумы для лучей разного цвета пространственно разойдутся, и на экране наблюдаются дифракционные спектры. Согласно условию максимума (166) большие длины волн дадут максимумы под большими углами, поэтому дифракционные спектры начинаются фиолетовым и заканчиваются красным цветом. В формуле (166) т - порядок спектра.

6.5.5 Дифракция на пространственной решётке. Формула Вульфа-Брэггов

Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения. Кристал­лы, являясь трехмерными пространственными решетками, имеют постоян­ную порядка 10^{-10 м и, следовательно, непригодны для наблюдения дифракции в видимом свете (}l » 5^.10^{-7 м). Эти факты позволили немецкому физику М. Лауэ (1879—1960) прийти к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с} l рентгеновского излучения (» 10^-12¸10^{-8 м).}

Простой метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен независимо друг от друга Г. В. Вульфом (1863—1925) и английс­кими физиками Г. и Л. Брэггами (отец (1862—1942) и сын (1890—1971)). Они пред­положили, что дифракция рентгеновского излучения является результатом его отраже­ния от системы параллельных кристаллографических плоскостей (плоскостей, в кото­рых лежат узлы (атомы) кристаллической решетки). Представим кристаллы в виде совокупности параллельных кристаллографических плоскостей (рисунок 48), отстоящих друг от друга на расстоянии d. Пучок параллельных монохроматических рентгеновских лучей (1,2) падает под углом скольжения q (угол между направлением падающих лучей и кристаллографической плоскостью). Рентгеновские лучи возбуж­дают атомы кристаллической решетки, которые становятся источниками когерентных вторичных воли 1' и 2'. Вторичные волны интерферируют между собой, подобно вторичным волнам от щелей дифракционной решетки. Максимумы интенсивности (дифракционные мак­симумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направление удовлет­воряют формуле Вульфа – Брэггов

2dsinq = ml , ( m =1,2,3,…) (168)

т. е. при разности хода между двумя лучами, отраженными от соседних кристалло­графических плоскостей, кратной целому числу длин волн l, наблюдается дифракцион­ный максимум.

При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобыее наблюдать, надо, повора­чивая кристалл, найти угол скольжения(q), удовлетворяющий формуле Вульфа-Брэггов. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться непрерывным рентгеновским спектром, испускаемым рентгеновской трубкой. Для таких условий опыта всегда найдутся длины волн l, удовлетворяющие условию (168).

Формула Вульфа — Брэггов используется при решении двух важных задач:

1. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристал­лической структуре неизвестного строения и измеряя q и m, можно найти межплоскостное расстояние (d), т. е. определить структуру вещества. Этот метод лежит в основе рентгеноструктурного анализа. Формула Вульфа—Брэггов остается справедливой и при дифракции электронов и нейтронов. Методы исследования структуры вещества, основанные на дифракции электронов и нейтронов, называются соответственно электронографией и нейтронографией.

2. Наблюдая дифракцию рентгеновских лучей неизвестной длины волны на кри­сталлической структуре при известном d и измеряя q и m, можно найти длину волны падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спектроскопии.