Способ абсолютных разниц
Алгоритм решения для двухфакторной мультипликативной модели вида 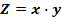 представлен ниже.
представлен ниже.
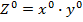
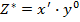
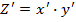
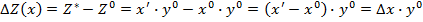
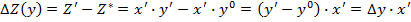
Используем формулы способа абсолютных разниц для предыдущего числового примера.
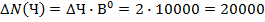
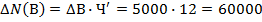
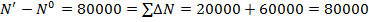
Способ имеет тот же недостаток, то есть количественные результаты зависят от последовательности подстановки, кроме того, данный способ пригоден только для двухфакторных мультипликативных и кратных моделей.
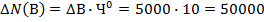
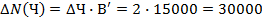
Влияние последовательности подстановки может быть устранено введением в расчетные формулы так называемого неразложимого остатка, тогда формулы для способа абсолютных разниц примут вид:
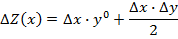
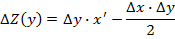
Или другой вариант, более легкий для запоминания.
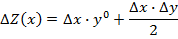
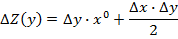
Выполним расчет по этим формулам.
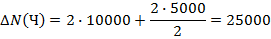
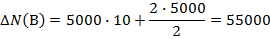
При использовании этих формул результаты расчета не зависят от последовательности замены факторов. В тех случаях, когда количество факторов более двух и способ абсолютных разниц не применяется, может быть использован прием взвешенных конечных разностей. Его суть — величина влияния каждого фактора определяется по всем возможным подстановкам, а затем полученные результаты усредняются.
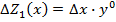
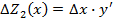

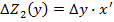
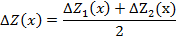
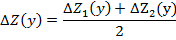
Определяем с помощью этого приема влияние факторов для предыдущего примера.
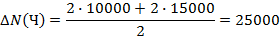
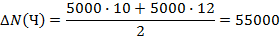
80000=80000
При большом количестве факторов способ становится весьма трудоемким и поэтому используется редко.
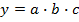
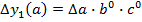
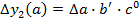


Логарифмический способ
Достоинство этого способа в том, что он позволяет определить влияние любого количества факторов на результативный показатель, причем без установления очередности подстановок. Способ применим к мультипликативным и кратным моделям. Рассмотрим мультипликативную модель вида 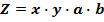 и представим ее в виде
и представим ее в виде
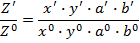
Прологарифмируем это выражение
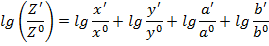
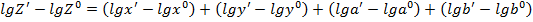
Умножим это уравнение на дробь 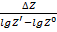 и получим
и получим
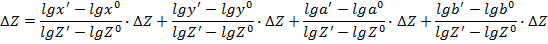
В окончательном виде это уравнение можно записать так:
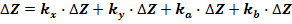 ,
,
Где 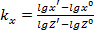 и т.д.
и т.д.
Коэффициенты kx, ky, ka, kb представляют собой удельные веса, влияние каждого фактора на результативный показатель.
Рассмотрим применение данного способа на предыдущем числовом примере.
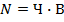
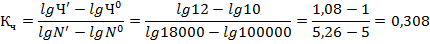
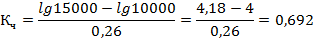
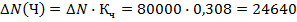
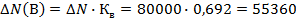

Полученные значения несколько отличаются от значений, полученных способом абсолютных разниц с неразложимым остатком из–за округления логарифмов.
Дата добавления: 2015-07-18; просмотров: 2053;
