Резервирование без восстановления

Под резервированием без восстановления понимается определение характеристик надежности резервных групп при следующих условиях:

а) элемент после отказа не восстанавливается;

б) замена основного элемента резервным осуществляется мгновенно;

в) отказ системы наступит тогда, когда откажет последний элемент резервной группы.

Рассмотрим, исходя из вышеуказанных предпосылок, различные виды резервирования.

а. Нагруженный резерв. В случае нагруженного резерва запасной элемент работает в том же режиме, что и основной, как до включения его вместо основного, так и после его включения. На практике это, как правило, не выполняется, но нам необходимо это оговорить, чтобы не усложнять выводы. В этом случае мы считаем, что надежность элемента не зависит от того, в какой момент резервный элемент переходит в рабочее состояние.

Пусть резервная группа состоит из одного основного элемента — 1 (рис. 4.1) и п—1—резервных. Обозначим через

p₁(t); p₂(t)…p_n(t)

надежности соответствующих элементов, а их ненадежности через

q₁(t); q₂(t)…q_n(t).

Резервные элементы

Рис. 4.1. Схема резервирования

Здесь и в дальнейшем под надежностью понимается вероятность безотказной работы в течение заданного времени, а под ненадежностью, — вероятность отказа за то же время. Их взаимосвязь:

q_л=1-p_n (4.1)

Пусть P_n(t) - надежность резервной группы;

Q(t) ненадежность резервной группы.

Отказ наступает тогда, когда выходит из строя последний из работающих элементов. Поэтому для того, чтобы в течение времени t отказала резервная группа, нужно чтобы в течение этого времени отказали все элементы. Так как все отказы независимы, то по теореме умножения вероятностей получим

Q_n(t)= q₁(t)× q₂(t) …q_n(t ) (4.2)

Соответственно надежность будет равна

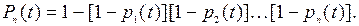(4.3)

Из формул (4.2) и (4.3) следует, что надежность резервной группы не зависит от порядка включения резервных элементов, и от того, как менялись функции надежности элементов до данного момента. Если все элементы имеют одинаковую надежность, то

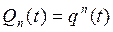(4.4)

где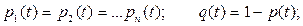

Q(t) — ненадежность группы;

п — в формуле означает кратность резерва.

Соответственно

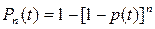(4.5)

Формула (4.4) легко разрешается относительно входящих в нее членов.

Решим ряд задач.

Задача № 1. Задана ненадежность элемента q(t) и требуется найти такое число резервных элементов, при котором ненадежность системы Q_n(t) не будет превосходить заданной величины Q. Из неравенства

qⁿ £ Q

следует, что

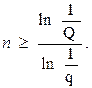(4.6)

Задача № 2. Задано число резервных элементов; какова должна быть надежность каждого элемента при заданной Q_n(t) = Q.

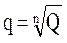(4.7)

Для случая экспоненциального закона

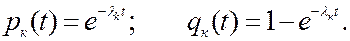
Заметим: если надежность элементов близка к 1, то

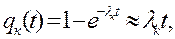(4.8)

и тогда

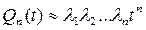, (4.9)

а для равнонадежных элементов

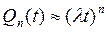, (4.10)

Относительная ошибка в формуле (4.10) не превышает

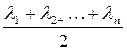t

Формулы (4.9) и (4.10) удобны, когда заданы не надежность, а интенсивность отказов l_к. Среднее время работы резервной группы

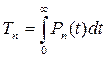. (4.11)

Если надежности элементов заданы аналитически, то среднее время во многих случаях вычисляется в конечном виде.

1. Экспоненциальный закон

Не приводя вывода формулы, укажем ее в конечном виде

(4.12)

Так среднее время работы одного элемента Т 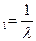, то

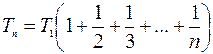(4.13)

Если «n» велико, то среднее время можно вычислить приближенно

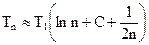, (4.14)

где С = 0,57712—постоянная Эйлера.

2. Закон Вейбулла.

Для случая равных надежностей

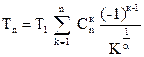(4.15)

где закон P_n (t) = exp [- lt^a].

C_n^к – число сочетаний «n» по «k».

Среднее время работы резервной группы может быть определено по результатам испытаний.

Пусть испытаны N одинаковых элементов и получили величины

O < t₁ < t₂ <…< t_N

Помня, что эмпирическая функция надежности

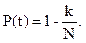(4.16)

k – число отказов, случившихся до момента t.

Тогда из формулы (4.11) получим

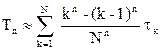(4.17)

Данные формулы можно применять с определенными ограничениями, в силу ряда допущений при выводе. Главное из них – действие законов надежности на малых интервалах t, а Т_n требует для определения значительных интервалов. Поэтому формула (4.17) применима для ограниченного круга элементов.

Для большинства элементов рекомендуется приближенная формула

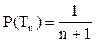(4.18)

б. Ненагруженный резерв. Ранее уже упоминалось, что в случае ненагруженного резервирования резервные элементы, пока работает основной, выключены и включаются поочередно, как только рабочий элемент выйдет из строя.

При рассмотрении этого вопроса делаются следующие допущения:

1. Элемент, находящийся в резерве, не может отказать (до включения в работу).

2. Надежность элемента в нерабочем состоянии не изменяется (на практике это не всегда верно).

3. Время замены элемента (переключения) весьма мало t_n »0.

4. Считаем, что переключающее устройство абсолютно надежно.

Пусть система имеет один основной и п —1 резервных элементов.

Обозначим через р(t) надежность k-го элемента по порядку, а через q_к(t) его ненадежность.

Основной элемент, проработав некоторое случайное время t₁, выходит из строя и на его место становится первый резервный элемент, который работает случайное время t₂ и т. д.

После выхода из строя последнего резервного элемента, проработавшего случайное время t_n, выйдет из строя и вся резервная группа.

Таким образом, случайное время жизни резервной группы равно

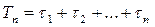(4.19)

величины t_к независимы и

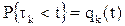
Обозначим через Q_n(t) резервной группы. Функция Q_n(t) как закон распределения суммы п независимых слагаемых определяется из формулы

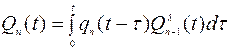, (4.20)

Q₁(t) = q₁(t)

Последовательно применяя формулу (4.20) для п=2,3,4...., можно вычислить точно или приближенно величину ненадежности Q_n(t).

Среднее время жизни резервной группы

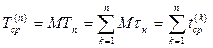(4.21)

В частности, если элементы равнонадежные, то

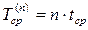(4.22)

Предположим, что надежности резервных элементов подчинены экспоненциальному закону

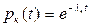
Тогда, для случаев, когда 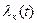малы, можно пользоваться приближенной формулой с достаточной для практики точностью

. (4.23)

В ней

.

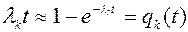Следовательно, формулу (4.23) можно записать в виде

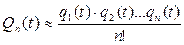(4.24)

Сравнивая формулу (4.24) с формулой (4.2), можно получить наглядное представление, во сколько раз ненагруженный резерв, который нередко в технической литературе называют холодным, выгоднее нагруженного (горячего) резерва

[Q_n(t)]_х.р. – ненадежность холодного резерва.

[Q_n(t)]_г.р. – ненадежность горячего резерва.

Как видно из соотношения, при ненагруженном резервировании, ненадежность меньше, чем при нагруженном в n! раз.

Чем больше кратность резервирования, тем более выигрыш в среднем времени работы. При

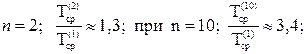
Если ненадежности всех элементов равны и подчинены экспоненциальному закону, для которого 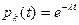, то для этого простого случая ненадежность резервной группы определится по формуле

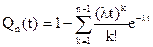(4.25)

Формула (4.25) достаточно сложна для вычислений. Вместо нее рекомендуется приближенная формула, более удобная для вычислений

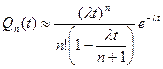(4.26)

Если lt<<1, то можно пользоваться совсем простой приближенной формулой

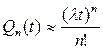(4.27)

Величина Q_n(t) вычисляется и при нормальном распределении. Здесь эти расчеты не приводятся.

В большинстве случаев величину Q_n(t) в конечном виде не удается вычислить. Поэтому основной интерес приобретают приближенные методы оценки надежности в этих случаях. Они достаточно хорошо разработаны, но в данной работе не приводятся.

в. Облегченный резерв. Во многих случаях невыгодно применять нагруженный резерв из-за недостаточного выигрыша в надежности. Вместе с тем, бывает и так, что нельзя применять ненагруженный резерв в силу того, что некоторые элементы после включения требуют конечного времени для достижения своих характеристик до рабочих значений — «разогрева» (например, двигатели внутреннего сгорания).

В подобных случаях применяют облегченный резерв, сущность которого изложена выше.

Пусть:

1. Резервная группа состоит из одного основного и п—1 резервных элементов.

2. P_к^(н) (0—надежность k-го элемента в нерабочем состоянии.

3. Р_к^(р)(t, t) —условная вероятность того, что k-ый элемент (резервный) не откажет, находясь в рабочем состоянии на участке времени (t, t) при условии, что он не отказал на .участке (0, t), находясь в нерабочем состоянии.

4. t—момент включения элемента.

5. Каждый резервный элемент включается в тот момент, когда откажет последний (по времени) из предыдущих элементов. Обозначим через t₁,t₂,t₃,…,t_n случайные времена работы основного и резервных элементов.

Пусть также

T_к = max T_i

1 £ i £ k

Очевидно, что в момент T_к происходит включение в рабочее состояние очередного (k+l)-ro элемента. Рассмотрим функции

Q_к(t) = P{ T_к < t}

Напомним, что

Q₁(t) —ненадежность основного элемента.

Q_к(t)—ненадежность резервной группы из основного и (k—1)-го элемента (резервного).

Q_n(t)—искомая ненадежность резервной группы.

Случайные времена t_к зависят друг от друга, т. к. время жизни резервного элемента зависит от того, когда он перешел в рабочее состояние, т.е. зависит от времени t_i . Две последовательные функции Q_к(t) и Q_к+1(t) будут связаны между собой следующим соотношением

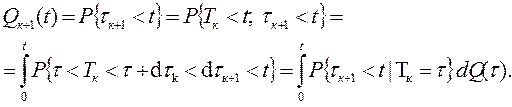
Вероятность

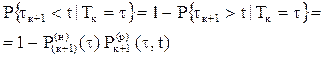(4.28)

Из формулы (5.28) следует:

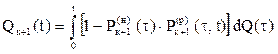(4.29)

Так как Q₁(t) — ненадежность основного элемента нам известна, то по этой формуле мы можем последовательно вычислить все функции Q_к(t). Однако вычисление затрудняет то обстоятельство, что обычно неизвестна функция p^(p)(t₁t). Ее опытное определение требует огромной статистики, т. к. функция зависит от двух аргументов.

Поэтому в качестве первого приближения предполагается, что пребывание элемента в облегченном состоянии не изменяет его надежности в рабочем состоянии.

Тогда

P_к^(р) (t, t) = P_к^(р) (t-t)

Мы уже отмечали, что нагруженный и ненагруженный резервы являются частными случаями облегченного резерва.

Для нагруженного резерва в обозначениях, принятых выше

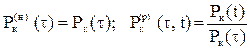
а для ненагруженного резерва

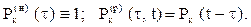
Для получения более простых формул предположим, что надежность элементов в рабочем и нерабочем состоянии подчиняется экспоненциальному закону и надежность элемента не зависит от времени пребывания в нерабочем состоянии.

Рассмотрим тот случай, когда надежности всех элементов одинаковы.

Пусть:

l — интенсивность отказа элемента в облегченном режиме.

L — интенсивность отказа элемента в рабочем состоянии.

Если к данному моменту времени отказал (k—1) элемент, то один из неотказавших элементов находится в рабочем режиме, а (n-k) элементов в облегченном режиме. Поэтому суммарная интенсивность отказа равна

l_к = L + (n – k)l (4.30)

Рассматриваемый процесс является частным случаем процесса гибели, рассматриваемого теорией массового обслуживания, и мы можем применить все формулы этого процесса. Из представлений теории массового обслуживания ненадежность резервной группы будет равна

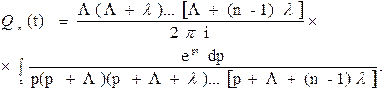
После ряда преобразований и подстановок получится следующее уравнение

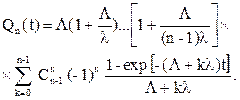(4.31)

При небольших n и надежностях элементов, не слишком близких к единице, можно пользоваться формулой (4.31).

В случае высоких надежностей можно использовать формулу:

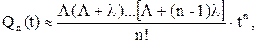(4.32)

Причем относительная ошибка не превосходит величины

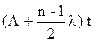
Наиболее общим случаем является тот, когда элементы имеют различные интенсивности отказов. Этот случай из-за сложности математического описания не рассматривается.

4.2. Некоторые принципиальные вопросы резервирования системы

а) Масштаб резервирования.

При резервировании системы можно резервировать либо отдельные элементы системы, либо блоки, входящие в систему, либо всю систему в целом.

Уровень, на котором производится резервирование, называется масштабом резервирования.

Чем большая часть системы резервируется как единое целое, тем больше масштаб резервирования.

Следует отметить, чем крупнее масштаб резервирования, тем меньше надежность резервированной системы. Это утверждение, данное нами без доказательства, имеет строгое математическое доказательство.

б) Скользящий резерв:

Если в системе имеются группы одинаковых элементов, то можно вместо резервирования каждого элемента, объединить все резервные элементы в группы и устроить т. н. скользящий резерв.

При этом имеется группа основных элементов и группа резервных элементов, которые включаются на место отказавших. При отказе рабочего элемента на его место включается первый резервный элемент из группы независимо от того, в каком блоке узле изделия произошел отказ.

Не приводя доказательств, укажем, что объединение резерва всегда повышает надежность системы в целом.

Следует отметить, что уменьшению масштаба резервирования н созданию скользящего резерва препятствуют технические причины. Это не так легко осуществить.