Обнаружение и исправление ошибок при обращении к ОП
При работе с полупроводниковой памятью не исключено возникновение различного рода отказов и сбоев. Причиной отказовмогут быть производственные дефекты, повреждение микросхем или их физический износ. Проявляются отказы в том, что в отдельных разрядах одной или нескольких ячеек постоянно считывается 0 или 1, вне зависимости от реально записанной туда информации. Сбой – это случайное событие, выражающееся в неверном считывании или записи информации в отдельных разрядах одной или нескольких ячеек, не связанное с дефектами микросхемы. Сбои обычно обусловлены проблемами с источником питания или с воздействием альфа-частиц, возникающих в результате распада радиоактивных элементов, которые в небольших количествах присутствуют практически в любых материалах. Как отказы, так и сбои крайне нежелательны, поэтому в большинстве систем основной памяти содержатся схемы, служащие для обнаружения и исправления ошибок.
Вне зависимости от того, как именно реализуется контроль и исправление ошибок, в основе их всегда лежит введение избыточности. Это означает, что контролируемые разряды дополняются контрольными разрядами, благодаря которым и возможно детектирование ошибок, а в ряде методов – их коррекция.
На рисунке 3.10 показано, каким образом осуществляются обнаружение и исправление ошибок. Перед записью М-разрядных данных в память производится их обработка, обозначенная на схеме функцией «f», в результате которой формируется добавочный К-разрядный код. В память заносятся как данные, так и этот вычисленный код, то есть (М + К)-разрядная информация. При чтении информации повторно формируется К-разрядный код, который сравнивается с аналогичным кодом, считанным из ячейки. Сравнение приводит к одному из трех результатов:
1. Не обнаружено ни одной ошибки. Извлеченные из ячейки данные подаются на выход памяти.
2. Обнаружена ошибка, и она может быть исправлена. Биты данных и добавочного кода подаются на схему коррекции. После исправления ошибки в М-разрядных данных они поступают на выход памяти.
3. Обнаружена ошибка, и она не может быть исправлена. Выдается сообщение о неисправимой ошибке.

Рис 3.10. Общая схема обнаружения и исправления ошибок
Коды, используемые для подобных операций, называют корректирующими кодами или кодами с исправлением ошибок. Одним из таких кодов является код Хэмминга.
Код Хэмминга является групповым систематическим кодом. В систематическом коде позиции информационных и контрольных разрядов постоянны. Такой код строится путем добавления m информационным разрядам k контрольных разрядов. Общее количество разрядов кодового слова  .
.
Минимальное количество контрольных разрядов К, необходимых для построения кода Хэмминга, обнаруживающего одиночную ошибку (кодовое расстояние d=3), определяется из уравнения
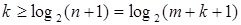
Все m информационных разрядов разбиваются на k контрольных групп, являющихся взаимно пересекающимися подмножествами. Это означает, что определенный информационный разряд может входить в одну или несколько контрольных групп.
Каждый контрольный разряд относится только к отдельной контрольной группе (определенному подмножеству).
При формировании кода (перед его записью в ОП) в контрольные разряды записываются символы 0 или 1, являющиеся дополнениями до четности числа единиц в контролируемых ими подмножествах.
Модифицированный код Хэмминга имеет кодовое расстояние d=4, что позволяет обнаруживать и корректировать одиночные ошибки и обнаруживать двойные.
Для образования модифицированного кода Хэмминга в разрядную сетку вводят дополнительный контрольный разряд для проверки на четность общего количества единиц во всем кодовом слове, включая все контрольные разряды.
Правила построения и использования кода Хэмминга рассмотрим на примере, для случая:
1. общее количество разрядов кодового слова 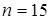 ;
;
2. количество контрольных разрядов 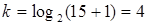 ;
;
3. количество информационных разрядов 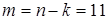 .
.
Первым этапом построения кода Хэмминга является разбиение разрядов кодового слова на взаимно пересекающиеся подмножества. За каждым подмножеством закрепляется контрольный разряд четности, дополняющий до четного количество единиц в разрядах кодового слова, включенных в данное подмножество.
Контрольные разряды имеют номера 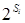 , где
, где 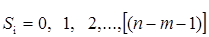 . В рассматриваемом примере контрольные разряды имеют номера: 1, 2, 4, 8, т.е. располагаются в 1, 2, 4 и 8 разрядах кодового слова при нумерации его разрядов слева направо: 1, 2, 3, ... , 15.
. В рассматриваемом примере контрольные разряды имеют номера: 1, 2, 4, 8, т.е. располагаются в 1, 2, 4 и 8 разрядах кодового слова при нумерации его разрядов слева направо: 1, 2, 3, ... , 15.
| к1 | к2 | к3 | к4 |
Формирование контролируемых подмножеств проведем на основании анализа номеров разрядов кодового слова при записи их в двоичной системе счисления. Все разряды кодового слова, имеющие единицу в первом разряде своего номера, включаются в подмножество Е1, во втором – в подмножество Е2 и т.д.
В таблице 3.1 показано закрепление разрядов кодового слова за подмножествами. Для первого подмножества контрольным разрядом является первый разряд кодового слова – к1, для второго подмножества – второй разряд кодового слова – к2, для третьего – четвертый разряд к3 и для Е4 – восьмой разряд к4.
Таким образом, в подмножества по Хэммингу входят следующие разряды кодового слова:
Е1={1, 3, 5, 7, 9, 11, 13, 15}
E2={2, 3, 6, 7, 10, 11, 14, 15}
E3={4, 5, 6, 7, 12, 13, 14, 15}
E4={8, 9, 10, 11, 12, 13, 14, 15}
Из приведенной схемы видно, что контрольные разряды (подчеркнуты) входят только в контролируемые ими подмножества и начинают эти подмножества. Другие разряды могут входить в несколько подмножеств, (например 15 – во все четыре).
Таблица 3.1.
Закрепление разрядов кодового слова
| Номера разрядов кодового слова | Подмножества по Хэммингу | |||||
| Десятичный номер | Двоичный номер | E4 | E3 | E2 | E1 | |
| (к1) | + | |||||
| (к2) | + | |||||
| + | + | |||||
| (к3) | + | |||||
| + | + | |||||
| + | + | |||||
| + | + | + | ||||
| (к4) | + | |||||
| + | + | |||||
| + | + | |||||
| + | + | + | ||||
| + | + | |||||
| + | + | + | ||||
| + | + | + | ||||
| + | + | + | + |
При записи числа в коде Хэмминга контрольные разряды заполняются таким образом, чтобы сумма единиц по 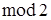 информационных разрядов каждого подмножества ES и его контрольного разряда равнялась нулю.
информационных разрядов каждого подмножества ES и его контрольного разряда равнялась нулю.
При схемной реализации контроля по коду Хэмминга устройство контроля должно содержать следующие основные узлы:
- приемный регистр на  разрядов;
разрядов;
- схемы сверток по 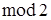 для каждого из подмножеств с целью образования контрольных кодов (кодирующие устройства);
для каждого из подмножеств с целью образования контрольных кодов (кодирующие устройства);
- схема свертки по 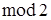 , охватывающая все n разрядов для обнаружения двойной ошибки;
, охватывающая все n разрядов для обнаружения двойной ошибки;
- схемы сравнения контрольных разрядов, получаемых при записи и после считывания числа из ОП, для образования синдромов ошибок;
- схемы обнаружения места одиночной ошибки и ее инвертирования.
Перед записью информации в ОП кодирующее устройство определяет значения контрольных разрядов и записывает их в соответствующие биты слова.
Пусть значения информационных разрядов передаваемого слова А равны: 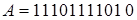 .
.
1. Запишем число, пропуская позиции контрольных разрядов:
Таблица 3.2.
| Номера разрядов | к1 | к2 | к3 | к4 | |||||||||||
| Код числа A |
2. Вычислим первый контрольный разряд. В первое подмножество входят разряды 3, 5, 7, 9, 11, 13, 15. 3, 5, 9 и 11 разряды равны единице, а остальные – нулю. Следовательно к1=0. Аналогично получаем значения остальных контрольных разрядов.
C учетом контрольных разрядов код числа А будет иметь вид, приведенный в таблице 3.3.
Таблица 3.3.
| Номера разрядов | к1 | к2 | к3 | к4 | |||||||||||
| Код числа A |
Контрольные разряды к1, к2, к3, к4 записаны в 1, 2, 4, 8 разряды кодового слова А. Цифры в контрольных разрядах по каждому подмножеству Е1, Е2, Е3, Е4 дополняют до нечетного значения число единиц в соответствующем подмножестве. Число А вместе с контрольными разрядами записывается в оперативную память.
Пример 1. Пусть значения информационных разрядов передаваемого числа 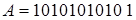 .
.
C учетом контрольных разрядов код числа А будет иметь вид, приведенный в таблице 3.4.
В процессе хранения или считывания этого числа из ОП может произойти искажение информации. Теория и практика показывают, что наиболее вероятны одиночные ошибки.
После считывания числа А из ОП вновь выделяются контрольные разряды к'1, к'2, к'3, к'4 и поразрядно сравниваются с первичными контрольными разрядами к1, к2, к3, к4, выделенными перед записью числа А в ОП.
Таблица 3.4.
| Номера разрядов | к1 | к2 | к3 | к4 | |||||||||||
| Код числа A |
Если сравниваемые контрольные разряды равны, ошибка отсутствует. В противном случае – в считанной информации имеется ошибка. Одиночные ошибки могут быть исправлены путем определения разряда числа, содержащего ошибку и инверсии его содержимого.
Пример 2. Введем ошибку в 13 разряд числа А путем замены 0 на 1. Код считанного числа А' с ошибкой приведен в таблице 3.5.
Таблица 3.5.
| Номера разрядов | к1 | к2 | к3 | к4 | |||||||||||
| Код числа A' |
Вычислим значения контрольных разрядов для считанного числа А с использованием подмножеств по Хэммингу.
Отметим, что 13-й разряд входит только в подмножества Е1, Е3, Е4, следовательно, произойдет инверсия контрольных разрядов (определенных для числа А) только в данных подмножествах. Получим: к'1=1, к'2=1, к'3=1, к'4=0.
Сложим по 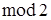 одноименные контрольные разряды кодового слова (числа А) и числа А'. В результате получим номер разряда кодового слова (числа А'), содержащего ошибку 13 разряд (D16 = 1310).
одноименные контрольные разряды кодового слова (числа А) и числа А'. В результате получим номер разряда кодового слова (числа А'), содержащего ошибку 13 разряд (D16 = 1310).
контрольные разряды числа А:
к'4=1, к'3=0, к'2=1, к'1=0
контрольные разряды числа А':
к'4=0, к'3=1, к'2=1, к'1=1
Номер разряда числа А', содержащего ошибку:
1 1 0 1 = 1310
Рассмотренный код Хэмминга имеет d = 3 и позволяет обнаруживать и корректировать одиночную ошибку. Обнаружение двойной ошибки возможно при использовании модифицированного кода Хэмминга, с кодовым расстоянием d = 4.
Дата добавления: 2015-07-18; просмотров: 1257;
