СТАТИСТИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ

Прогнозирование, основанное на использовании методов статистического анализа ретроспективных данных, допустимо в том случае, когда между прошлым и будущим имеется определенная причинно-следственная связь. Можно утверждать, что анализ ретроспективных данных служит надежной основой для прогноза будущих действий, однако не следует забывать, что прогностические оценки, полученные методом статистического анализа, подлежат корректировке, если известны факторы, влияние которых с той или иной вероятностью ожидается в будущем.

Маркетинговые исследования поставляют необходимую статистическую информацию для применения методов статистического анализа при разработке прогнозов.

Алгоритм построения прогнозов методом статистического анализа состоит из следующих шагов:

· строится график зависимости спроса от времени;

· на основе визуального изучения графика делается предположение об аналитической форме кривой, которая наилучшим образом способна аппроксимировать ломаную на графике;

· применяется метод наименьших квадратов (МНК), наиболее часто используемый метод построения прогнозирующей функции;

· рассчитывается среднее значение погрешности полученных прогнозных оценок;

· принимается решение об использовании или не использовании выбранной кривой для построения прогноза.

Наиболее часто для построения прогнозирующей функции используют линейную функцию, параболу, гиперболу, многочлены более высоких порядков. При выборе прогнозирующей функции предпочтение отдается той аналитической форме, которая обеспечивает минимальное из стандартных отклонений как погрешность оценки аппроксимации. Поэтому следует испытать несколько различных форм прогнозирующей функции и выбрать наилучшую в соответствии с критерием минимизации стандартного отклонения.

МЕТОДЫ «СТОИМОСТЬ–ЭФФЕКТИВНОСТЬ» И «ЗАТРАТЫ–ПРИБЫЛЬ»

В основном метод «стоимость–эффективность» требует оценки общих издержек и общих доходов для каждой из нескольких альтернатив. Затем вычисляется отношение общих доходов к общим издержкам для определения дохода на единицу затрат. Далее выбирается альтернатива с наибольшим отношением доходов к издержкам, конечно, в предположении, что общие издержки находятся в приемлемых пределах, определяемых специалистами по планированию исходя из ограниченности ресурсов.

Как показывает опыт, наиболее эффективные проекты нередко оказываются и наиболее дорогостоящими. Естественно, что если бы среди рассматриваемых предложений оказался проект, ожидаемая эффективность которого превосходит ожидаемую эффективность других проектов, а стоимость – меньше стоимости других проектов, то задача выбора решалась бы просто. Такой проект и является наиболее предпочтительным.

Однако в реальной практике принятия решений этот случай крайне редкий. Поэтому, для того чтобы выбрать действительно наиболее предпочтительный альтернативный вариант, необходим дополнительный анализ – дополнительная многокритериальная, а в рассматриваемом случае двухкритериальная оценка.

Отметим, что в анализе «стоимость–эффективность» не делается попытка найти одну общую меру, единственную количественную оценку, которая позволила бы сопоставить по предпочтительности (ранжировать) рассматриваемые альтернативные варианты проектов.

Не менее часто в практике принятия решений используется так называемый метод «затраты–прибыль», при котором рассматриваются различные виды «прибыли», под которыми понимаются различные критерии, характеризующие проект, причем необязательно экономической природы.

Одно из основных требований этого метода, заложенное в алгоритме принятия решений, – возможность складывать различные виды «прибыли» с фиксированными числовыми коэффициентами, получая единую составную величину – «прибыль», характеризующую проект.

В частности, поскольку даже с экономической точки зрения проекты могут характеризоваться различными критериями, составную «прибыль» могут образовывать такие показатели, как потоки платежей, внутренняя норма окупаемости, срок окупаемости и т.д.

Наиболее трудным при использовании данного метода является надежное определение коэффициентов, отражающих степень вклада каждого из показателей в составную «прибыль».

После того как составные «прибыли» для проектов определены, получаем двухкритериальную задачу выбора. Этот прием позволяет сводить многокритериальную задачу, при числе критериев больше двух, к двухкритериальной.

Одним из возможных способов практического решения задачи многокритериального оценивания в методах «стоимость–эффективность» и «затраты–прибыль» является назначение желательных уровней получаемых прибылей, достигаемых при условии, что необходимые при этом затраты не превосходят заданный уровень.

Наиболее предпочтительные проекты определяются с помощью варьирования желательных уровней получаемых «прибылей» при фиксированном объеме затрат.

Для метода «затраты–прибыль» более характерно стремление к получению числовых характеристик, позволяющих сопоставлять по предпочтительности предлагаемые проекты.

Здесь имеется в виду стремление не только определить составную «прибыль», т.е. количественное значение, характеризующее в некотором смысле эффективность проекта, но и ранжировать проекты по предпочтительности на основании количественных оценок.

В методе «затраты–прибыль» для каждого проекта с номером k, рассчитав значение составной прибыли B_k и требуемых затрат C_k, можно рассчитать и величину отношения 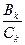, характеризующую ожидаемое значение составной «прибыли» на единицу затрат.

Далее, упорядочив проекты по убыванию значения отношения 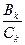, получим ранжирование рассматриваемых проектов по степени предпочтительности, имея в виду, что наиболее предпочтительным проектом является проект с наибольшей ожидаемой составной «прибылью», полученной на единицу затрат.

Вторым по предпочтительности является проект, обладающий вторым по величине значением ожидаемой составной прибыли, получаемой на единицу затрат, и т.д.

Для того чтобы сформировать портфель проектов, обладающих максимальной ожидаемой составной «прибылью», необходимо последовательно включать в такой перечень проекты по убыванию отношения 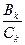до тех пор, пока не будет исчерпан выделенный на финансирование проектов объем средств С^*.

Если проекты, включенные в перечень согласно изложенному выше алгоритму, полностью исчерпывают С^*, то получаем оптимальное решение задачи распределения ресурсов. В противном случае необходимо дополнительно учитывать возможное наиболее эффективное использование остатка выделенного объема финансирования.