Каналов

1.6. Модели каналов

Как было упомянуто во введении, каналы передачи информации могут классифицироваться по различным признакам. В настоящем курсе их классификация осуществляется по характеру сигналов на их входе и выходе. С этой точки зрения каналы подразделяются на дискретные и непрерывные.

Точное математическое описание любого реального канала является весьма сложным. Вместо этого можно использовать упрощенные математические модели, которые позволяют выявить важнейшие закономерности реального канала.

Основные требования к модели:

- приемлемая точность;

- общий характер, чтобы при переходе от одного канала к другому модель не менялась, а менялись бы только параметры модели;

- сравнительная простота, т.е. небольшое число параметров, описывающих модель.

1.6.1. Модели дискретных каналов

Начнем рассмотрение с моделей дискретного канала, помня (см. введение), что в его состав всегда входит и непрерывный канал. На входе и выходе дискретного канала наблюдаются дискретные сигналы, как по уровням, так и по состояниям информационного параметра во времени, или те или иные символы из конечного алфавита.

Дискретный канал считается математическим описанным, если заданы:

1) алфавит кодовых символов на входе 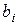(i=1,2,3 . . . , m) с их вероятностями ,

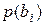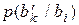2) алфавит кодовых символов на выходе (k=1,2,3 . . . , m^!) и значения условных вероятностей , т.е. вероятностей того, что на выходе канала появится символ при условии, что на вход канала подан символ .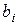

Дискретный канал называется однородным или стационарным, если вероятности 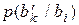для каждой пары i и k не меняются во времени.

Рассмотрим наиболее простые и широко используемые модели дискретных каналов.

1. Симметричный канал без памяти.Этот канал определяется как дискретный канал, в котором каждый переданный символ может быть принят ошибочно с фиксированной вероятностью p и правильно с вероятностью q=1-p, причем в случае ошибки вместо переданного символа 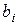может быть принят с равной вероятностью (свойство симметричности) любой другой символ 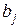из множества m символов. Таким образом, вероятность того, что принят символ 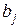, если был передан символ 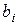, равна .

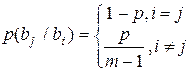Термин «без памяти» в названии модели канала означает, что вероятность ошибочного приема символа не зависит от предыстории канала, т.е. от того, какие символы передавались ранее и как они были приняты.

Вероятность того, что произошло 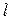каких угодно ошибок, расположенных как угодно на протяжении последовательности длины n, определяется формулой Бернулли 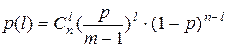, где - биномиальный коэффициент, равный числу различных сочетаний 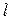ошибок в блоке длиной n. Эту модель называют также биномиальным каналом.

Для двоичного (m=2) симметричного канала без памяти вероятности переходов можно показать в виде графа (рис. 1.12).

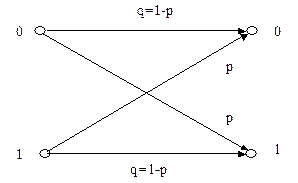
Рис. 1.12

2. Симметричный канал без памяти со стиранием.Эта модель канала отличается от предыдущей тем, что алфавит на выходе канала содержит 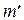>m символов, причем чаще всего 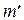= m+1 , т.е. выходной алфавит по сравнению с входным содержит один дополнительный символ, который можно обозначить «?». Этот символ появляется тогда, когда приемник не может надежно опознать принятый символ, в результате чего возникает отказ от решения или стирание, т.е. считается, что не принят никакой символ. Вероятность p_c стирания в данной модели постоянна и не зависит от передаваемого символа. За счет введения стирания удается значительно снизить вероятность ошибки. Для двоичного канала со стиранием граф переходных вероятностей можно представить следующим образом (рис. 1.13).

3. Несимметричный канал без памяти.Он отличается от симметричного тем, что в нем вероятность ошибки зависит от того, какой символ передается.

Для простейшего двоичного канала (m=2) это означает, что вероятность p(1/0) приема 1, если передавался 0, не равна вероятности p(0/1) приема 0, если передавалась 1, т.е. p(1/0) ¹ p(0/1). Граф переходных вероятностей для такого канала выглядит следующим образом (рис. 1.14).

Рис. 1.13

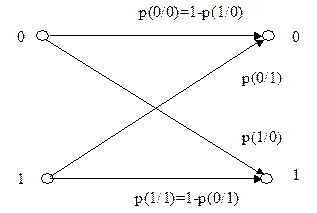
Рис. 1.14

4. Канал с памятью. Простейшей моделью дискретного канала с памятью является т.н. марковский канал. В этой модели вероятность ошибки образует простую цепь Маркова, т.е. зависит от того, правильно или ошибочно принят предыдущий символ, но не зависит от того, какой символ передается.

Рассмотренные выше модели отличаются исключительной простотой, поскольку единственным параметром канала, необходимым для определения всех характеристик системы является вероятность искажения символа, а ошибки считаются независимыми. Исследования реальных каналов показали, что статистика ошибок не удовлетворяет столь простой модели. Ошибки являются зависимыми и обладают ярко выраженной тенденцией к группированию или пакетированию. Эти исследования привели к тому, что в настоящее время насчитывается несколько десятков моделей каналов, более или менее удовлетворительно описывающих потоки ошибок в реальных каналах.

5. Модель Гилберта. Исторически первой моделью, учитывающей группирование ошибок, является модель Гилберта. В этой модели канал может находиться в одном из двух состояний – «хорошем», когда ошибки отсутствуют, и «плохом», когда возникают независимые ошибки с вероятностью p_{ОШ ПЛ}. Для описания модели необходимо задать еще вероятность p_ХП того, что при переходе к следующему биту хорошее состояние сменится на плохое, и вероятность p_ПХ того, что плохое состояние сменится на хорошее. Модель Гилберта удовлетворительно описывает лишь телефонные каналы, в которых преобладают длинные и плотные пакеты ошибок.

6. Модель Фройлиха-Беннета. Другой распространенной моделью является модель Фройлиха-Беннета. Она основана на следующих предположениях: а) ошибки группируются в пакеты; б) пакеты независимы; в) ошибки внутри пакета также независимы. Эта модель задается тремя параметрами:

-вероятностью появления пакета p_П, равной отношению числа пакетов к общему числу переданных бит;

-распределением вероятностей пакетов p_П(L) различной длины L;

-вероятностью ошибки внутри пакета p.

7. Модель Попова-Турина. Обобщением модели Фройлиха-Беннета является модель Попова-Турина, которая предполагает существование в канале независимо возникающих цепочек пакетов ошибок. Внутри цепочек независимо появляются пакеты ошибок. Внутри пакетов задается условная вероятность появления ошибок.

Все рассмотренные модели каналов, являясь моделями с постоянными параметрами, могут быть использованы для описания реальных каналов лишь на сравнительно коротких промежутках времени. Более близкой к реальности оказывается модель, параметры которой зависят от времени, т.е. нестационарная модель с переменными параметрами.

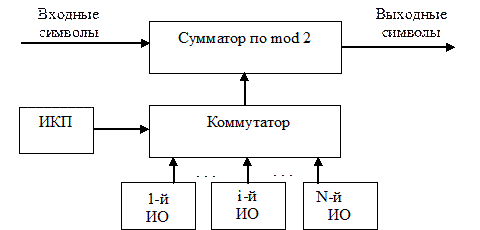
8. Кусочно-стационарной модели канала. Сложная нестационарная модель канала может быть представлена в виде более простой модели, параметры которой случайным образом изменяются во времени. Это осуществляется за счет декомпозиции единого источника ошибок на N составляющих, которые можно пронумеровать и поставить каждой в соответствие одно из значений дискретной совокупности параметров. Момент подключения той или иной составляющей источника ошибок (ИО), длительность интервала между переключениями и номер подключенной составляющей определяется источником коммутирующего процесса (ИКП). Эквивалентная схема определенной подобным образом кусочно-стационарной модели канала представлена на рис. 1.15.

Время, в течение которого к сумматору подключен i-й ИО, называется i-м стационарным состоянием. Разложение на N составляющих в значительной мере условно и может быть выполнено многими способами. Это обеспечивает определенную свободу при выборе моделей ИО и модели ИКП. Чем более простыми выбираются модели ИО, тем чаще должны происходить переключения, тем важнее становится роль ИКП и тем сложнее должна быть его модель. Целесообразен разумный компромисс: с одной стороны, модели ИО должны быть достаточно просты, чтобы можно было за короткое время производить расчеты, с другой стороны – описывать особенности поведения канала на достаточно больших отрезках времени, чтобы возможно проще задать модель ИКП. С этой точки зрения в качестве модели ИО можно использовать модель Гилберта, которая отражает процессы пакетирования ошибок и проста для расчетов. Модель ИКП, если стационарные состояния канала предполагаются достаточно продолжительными, в расчетах может быть представлена в виде вероятностей стационарных состояний.

Рис. 1.15

Таким образом, рассматриваемый подход, с одной стороны, позволяет строить модели, детально описывающие канал на длительных промежутках времени, с другой стороны, сложность расчетов по такой модели при рациональном выборе параметров лишь незначительно отличается по сложности от расчетов по каждой составляющей, что делает ее наиболее приемлемой для использования.

1.6.2. Модели непрерывных каналов

1. Идеальный канал без помех. В непрерывном канале действует непрерывный по структурному параметру сигнал, который называют также аналоговым сигналом. Часто непрерывный канал рассматривается как линейная система, описываемая либо импульсной, либо частотной характеристикой. Из такого описания следует, что в общем случае канал изменяет форму и спектр входного сигнала. Для многих систем передачи данных при передаче сигналов по непрерывному каналу важно, чтобы сохранялась форма передаваемых сигналов, что необходимо для правильного распознавания сигналов на приемной стороне канала. При таком ограничении передаваемый сигнал считается неискаженным, если, кроме линейного масштабного преобразования с коэффициентом k и задержки на некоторый интервал времени t, сигнал не претерпевает никаких изменений, т.е если выполняется равенство y(t)=kx(t-t), где y(t) –выходной сигнал, x(t) –входной сигнал. Такое возможно лишь в том случае, если АЧХ канала есть постоянная величина, а ФЧХ канала является линейной функцией частоты. В действительности такие характеристики непрерывного канала получить невозможно, в связи с чем эта модель канала носит названия идеального канала без помех. Она иногда используется для описания кабельных каналов.

2. Канал с аддитивным гауссовским шумом. Рассмотренная модель непригодна для описания реальных каналов в которых присутствуют аддитивные помехи. В этом случае используется модель, называемая каналом с аддитивным гауссовским шумом. Эта модель описывается выражением y(t)=kx(t-t)+n(t), где n(t) -гауссовский аддитивный шум с нулевым математическим ожиданием и заданной корреляционной функцией. Чаще всего в качестве такового рассматривается квазибелый или белый шум. Такая модель удовлетворительно описывает многие проводные каналы и радиоканалы при связи в пределах прямой видимости.

3. Канал с неопределенной фазой. Следующая модель, называемая каналом с неопределенной фазой, отличается от предыдущей тем, что в ней запаздывание t(t) является случайным процессом. Эта модель удовлетворительно описывает те же каналы, что и предыдущая, если фаза сигнала в них флуктуирует. Эти флуктуации могут вызываться небольшими изменениями свойств среды распространения сигнала, а также фазовой нестабильностью опорных генераторов.

4. Однолучевой гауссовский канал с общими замираниями. Если кроме флуктуации фазы имеет место и флуктуация амплитуды, т.е и k(t) является случайным процессом, то такая модель называется однолучевым гауссовским каналом с общими замираниями. Эта модель достаточно хорошо описывает многие каналы радиосвязи в различных диапазонах волн.

Для статистического описания непрерывного канала надо задать плотности вероятности 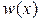входных сигналов 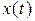и условные плотности вероятностей перехода 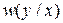, где 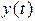- выходные сигналы.

Непрерывный канал называется однородным или стационарным, если плотности вероятности перехода 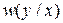не зависят от времени, и каналом без памяти, если значения выходного сигнала 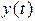в момент времени t зависят от значения входного сигнала 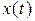в тот же момент времени. Если значения выходного сигнала 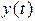в момент времени t зависят от значений входных сигналов и в предшествующие моменты времени, то такой канал называется каналом с памятью.