Лекция 7
Классификация
Помех
1.5. Классификация помех
Степень соответствия переданного и принятого сообщения определяется, главным образом, искажениями сигналов в канале и присутствующими в канале помехами.
Под искажениями понимаются нежелательные изменения формы передаваемых сигналов, которые вносятся самим каналом. При этом следует иметь в виду, что термин «искажения» относится к изменению формы сигнала в тех звеньях канала, которые по своему назначению не должны этого делать и ни в коей мере не относятся к звеньям канала, которые осуществляют целевые преобразования сигналов, невозможные без изменения их формы (например, модуляция и демодуляция).
Если искажения обусловлены известными характеристиками звеньев канала, то они могут быть, по крайней мере теоретически, устранены за счет введения соответствующей коррекции.
Помехи, в отличие от искажений, носят случайный характер и не могут быть полностью устранены. Помехой называется любое случайное воздействие на сигнал, которое ухудшает верность воспроизведения переданного сообщения. Помехи весьма разнообразны по своему происхождению и физическим свойствам.
В общем случае влияние помехи n(t) на сигнал u(t) можно выразить оператором z=y(u,n).
В частном случае, когда оператор y вырождается в сумму z=u+n, помеха называется аддитивной.
Аддитивные помехи по своей электрической и статистической структурам подразделяются на:
1) флуктуационные или распределенные по частоте и по времени,
2) гармонические или сосредоточенные по частоте,
3) импульсные или сосредоточенные по времени.
Флуктуационная помеха - это непрерывный во времени случайный процесс. Чаще всего его полагают стационарным и эргодическим с нормальным распределением мгновенных значений и нулевым средним. Энергетический спектр такой помехи в пределах анализируемой полосы частот полагают равномерным.
Гармоническая помеха - это аддитивная помеха, спектр которой сосредоточен в сравнительно узкой полосе частот, сопоставимой или даже существенно более узкой, чем полоса частот сигнала. Эти помехи полагают равномерно распределенными в полосе частот, т.е. вероятность появления этой помехи в некоторой полосе частот пропорциональна ширине этой полосы и зависит от среднего числа nгп помех, превышающих пороговый уровень средней мощности сигнала в единице полосы частот.
Импульсная помеха - аддитивная помеха, представляющая собой последовательность импульсов, возбуждаемых кратковременными ЭДС апериодического или колебательного характера. Моменты появления импульсной помехи полагают равномерно распределенными во времени. Это означает, что вероятность появления импульсной помехи в течение интервала времени Т пропорциональна длительности этого интервала и среднему числу nип помех в единицу времени, зависящему от допустимого уровня помех.
Если оператор y может быть выражен в виде произведения z=kn, где k(t) - случайный процесс, то помеху называют мультипликативной.
В реальных каналах обычно имеют место как аддитивные, так и мультипликативные помехи, т.е. z=ku+n.
Степень соответствия принятого сообщения переданному называется верностью. Количественная мера верности может быть определена по-разному, в зависимости от характера сообщений и требований получателя.
Если сообщение представляет собой дискретную последовательность элементов из некоторого конечного множества, то влияние помехи на передачу такого сообщения проявляется в том, что вместо фактически переданного элемента может быть принят какой-либо другой. Такое событие называется ошибкой.
В качестве количественной меры верности в этом случае может быть выбрана вероятность ошибки pош.
При передаче непрерывных сообщений степенью соответствия принятого сообщения 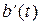 переданному
переданному 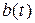 может служить их «разность». Часто используется критерий среднеквадратического отклонения
может служить их «разность». Часто используется критерий среднеквадратического отклонения  .
.
Количественную меру верности можно также определить как вероятность того, что отклонение 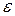 не превзойдет некоторого заранее заданного значения
не превзойдет некоторого заранее заданного значения 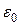 , т.е.
, т.е. 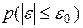 .
.
Дата добавления: 2015-07-14; просмотров: 1398;
