Вывод уравнения уровня программы.
Нередко требуется определить уровень программы непосредственно из ее реализации, не зная ее потенциального объема V* и не ссылаясь на возможное обращение к ней в виде вызова процедуры. Это можно сделать рассмотрев отдельно влияние операторов и операндов на уровень программы. Разумно предположить, что чем больше число уникальных операторов, используемых в реализации, тем ниже ее уровень. Но наименьшее возможное число уникальных операторов равно двум и эти два оператора суть символ функции и оператор присваивания или группировки, т.е. h1*= 2. С другой стороны, увеличение числа уникальных операторов беспредельно, поскольку на него нет ограничений ни в каком языке, в котором разрешено определение новых вложенных процедур, подпрограмм или переходов к помеченным участкам. Отсюда получаем следующее соотношение операторов
L ~ 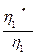 (3.3)
(3.3)
Операнды же не дают однозначного минимума по всем возможным алгоритмам поэтому к ним требуется иной подход. В этом случае достаточно заметить, что всякое повторение имени операнда является указанием на более низкий уровень реализации. Этот эффект можно измерить, взяв отношение числа простых операндов к общему числу операндов
L ~ 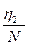 (3.4)
(3.4)
Объединяя уравнения (3.3) и (3.4), заметим, что коэффициент пропорциональности, являющийся константой должен равняться единице, поскольку в случае потенциального языка h1=h1*, h2=N2 и L=1. Тогда приходим к уравнению уровня программы
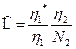 , (3.5)
, (3.5)
в котором символ ^ указывает на то, что уровень, определяемый этим выражением, служит аппроксимацией уравнения (3.1). На самом деле его можно было бы взять в качестве альтернативного определения уровня программы.
Возвращаясь к примерам программ для алгоритма Евклида, определим их уровень и его оценку для представлений на Паскале и СИ.
Паскаль: L = V* / V =11.6 / 254.4 = 0.0456; 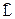 = 2*h2 /(h1* N2) = 2*6/(12*21) =0.0476
= 2*h2 /(h1* N2) = 2*6/(12*21) =0.0476
СИ: L = V* / V =11.6 / 224.8 = 0.0516; 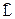 = 2*h2 /(h1* N2) = 2*6/(11*18) =0.0606 .
= 2*h2 /(h1* N2) = 2*6/(11*18) =0.0606 .
Дата добавления: 2015-08-26; просмотров: 968;
