Расчет времени, необходимого для программирования.

Рассмотрим понятие, введенное психологом Джоном Страудом в работе «Тонкая структура психологического времени». Дж.Страуд определил «момент» как время, требуемое человеческому мозгу для выполнения наиболее элементарного различения. Он обнаружил, что в течение времени бодрствования человек воспринимает эти «моменты» со скоростью «от пяти до двадцати раз» в секунду. Следует отметить, что в диапазон приведенных Страудом цифр попадает и число кадровв секунду, превращающее кинофильм из последовательности отдельных снимков в непрерывное изображение. Обозначая через S число страудовских «моментов» в секунду, мы можем записать

5 £ S £ 20 в сек.

В дальнейшем S называется числом Страуда. Естественно, что любой человек, занимающийся реализацией алгоритма, может в зависимости от степени своей сосредото-ченности отвлечь какую-то часть мысленных различений на посторонние предметы. Пользуясь терминологией вычислительной техники, можно сказать, что, если он находится «в режиме разделения времени», S представляет собой лишь верхнюю границу. С другой стороны, если программист выполняет эквивалент машинной операции «запретить все прерывания» и сосредоточивает внимание на программировании, то применимо действительное значение S.

Для того чтобы перевести в единицы времени уравнение (4.2), имеющее размерность двоичных разрядов или различений, разделим обе его части на число различений в единицу времени. В результате получим

T^ = 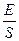= = 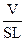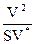(4.4)

Символ ^ здесь указывает на то, что с помощью этого уравнения вычисляется приближенное, а не наблюдаемое время программирования.Уравнение (4.4) можно выразить через основные параметры, если подставить в него вместо V правую часть уравнения (2.1), а вместо L - правую часть уравнения (3.5)

T = 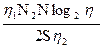(4.5)

При этом, естественно, 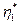=2.

В предыдущем выводе подразумевалось, что все программы совершенны, т. е. не имеют несовершенств. Хотя это допущение более или менее обосновано для опубли-кованных программ, оно необязательно. Поэтому откажемся от него по крайней мере в первом приближении, подставив 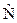вместо N в уравнение (4.5). Если при этом 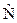задается уравнением длины, приходим к выражению

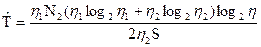, (4.6)

где, за исключением числа Страуда S, все параметры в правой части доступны непосред-ственному измерению для любой реализации алгоритма.