Ефективність обміну

У тій мірі, у якій граничні норми заміщення в учасників угоди розрізняються між собою, існує можливість взаємовигідного обміну і підвищення ефективності. І навпаки, якщо граничні норми заміщення є рівними для всіх пар товарів, що обмінюються:

MRS^A_XY = MRS^B_XY, (13.8)

то розподіл є ефективним і подальший взаємовигідний обмін є неможливим.

У дослідженні процесу обміну між споживачами А і В застосовується так звана “коробка Еджуорта”. Відкладемо у “коробці Еджуорта” криві однакової корисності (криві байдужості) споживача А U¹_A, U²_A, U³_A, U⁴_A. Очевидно, що вони будуть віддалятись від лівого нижнього кута (рис. 13.1). За аналогією побудуємо криві байдужості споживача В U¹_B, U²_B, U³_B, U⁴_B. Вони, в свою чергу, будуть віддалятись від правого верхнього кута. У загальному вигляді вся заштрихована на рис.13.1 ділянка описує всю множину взаємовигідних угод.

Товар Y Споживач В

О_B

U¹_B

E

U²_B

U³_B D U⁴_A

C

U⁴_B U³_A

F

U²_A

U¹_A

Q_A

Споживач А Товар Y

Рис. 13.1. Ефективність обміну

Розподіл продуктів є ефективним, коли увесь обсяг виробленої продукції розподіляється між споживачами таким чином, що не можна покращити стан одного з них, не погіршуючи стану іншого.

Щоб знайти всю множину можливих ефективних варіантів розподілу двох благ між двома споживачами, потрібно визначити всі точки взаємного дотику їх кривих байдужості. Поєднавши їх, отримаємо криву контрактів, чи договірну криву О_АО_В (рис. 13.2).

Крива контрактів – це множина можливих ефективних варіантів розподілу двох економічних благ між двома споживачами. Крива О_АО_В – множина точок, що відповідають розподілу благ, після якого взаємовигідний обмін втрачає сенс, тому що неможливі подальші взаємовигідні угоди. Множина таких розподілів має назву Парето-ефективною (Парето-оптимум) на ймення італійського економіста Вільфредо Парето, який запропонував цей критерій ефективності. Розподіл є Парето-ефективним, якщо товари неможна перерозподіляти таким чином, щоб покращити чиєсь положення, не погіршуючи положення інших. Точки F, C, D, E – Парето-ефективні. Рух у напрямку кривої контрактів підвищує загальний добробут, у той час як рух уздовж кривої контрактів лише перерозподіляє загальний добробут між учасниками угоди.

Товар Y Споживач В

О_В

О_А

Споживач А Товар Y

Рис. 13.2. Крива контрактів

На лінії контрактів виконується наведена раніше рівність (13.8):

MRS^A_XY = MRS^B_XY = MRT_XY,

де MRS – гранична норма заміни (субституції);

MRT – гранична норма трансформації.

Гранична норма трансформації показує мінімальну кількість одного товару, який необхідно принести у пожертву збільшенню виробництва іншого товару на одиницю.

Для досягнення ефективності по Парето необхідно усунути будь-які можливості отримання якої-небудь додаткової вигоди від обміну. Це і передбачає рівність граничних норм заміни одного товара іншим у всіх споживачів, що приймають участь в обміні. Дотик кривих байдужості означає рівність граничних норм заміни. В загальному вигляді це означає, що співвідношення цін товарів, що обмінюються, є рівним для всіх учасників угоди:

MRS^A_XY = 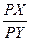= MRS^B_XY. (13.9)

Маючи множину точок, ефективних по Парето, можна побудувати криву споживацьких можливостей, чи, як її інакше називають, криву можливих корисностей. Відкладемо на вісі абсцис корисність споживача А, а на вісі ординат – корисність споживача В (рис. 13.3). Тоді крива контрактів може бути представлена як крива споживацьких можливостей О_ВЕСFКО_А.

U_B

O_A

K

F ̣N

C

A E

O_B U_A

Рис.13.3. Крива споживацьких можливостей

Точка О_В відображає максимальну корисність для споживача А, а точка О_А – максимальну корисність для споживача В. Точка А опиниться всередині межі споживацьких можливостей. Вона характеризує неефективний розподіл продуктів.

Будь-які угоди всередині заштрихованого простору покращують положення сторін. Переміщення в точку Е покращує положення споживача А, не погіршуючи положення споживача В. Рух у точку F покращує положення споживача В, залишаючи без змін положення споживача А. Досягнення точки С покращує положення обох.