Способы определения элементов приведения.
Величины e, e1, Θ, Θ1 необходимые для вычисления с и r называются элементами приведения. Для их определения чаще всего применяют графический способ.
Над центром пункта устанавливают центрировочный столик, на который прикрепляют лист бумаги. Затем с помощью вспомогательного теодолита проектируют на центрировочный лист центр пункта, ось вращения теодолита (если наблюдение ведется с сигнала) и ось визирного цилиндра. Проектирование выполняют при двух положениях круга с трех точек, расположенных так, чтобы проектирующие плоскости пересекались под углом 1200. Стороны треугольников погрешностей при проектировании точек С и Р не должны превышать 0,5 см, а для точки V – 1 см. Окончательное положение проекций точек С, Р и V намечают в центре треугольников погрешностей (рис. 2.8).
Линейные элементы приведения е и е1 измеряют с точностью до 1 мм. Для определения угловых элементов приведения Θ и Θ1, из точек Р и V c помощь визирной линейки прочерчивают направления на начальный пункт, после чего углы измеряют транспортиром. Для контроля прочерчивают направления еще на один из пунктов K, измеряют транспортиром углы NPK, NVK и сравнивают их с измеренными теодолитом.

Рис. 2.8.
Графический способ применяют в случаях, когда е и е1 небольшие.
Если е не вмещается на центрировочный лист, то его измеряют непосредственно рулеткой, как расстояние между нитью отвеса, установленного над центром пункта, и нитью отвеса теодолита. Угол измеряют непосредственно теодолитом.
4. Предварительная обработка триангуляция.
После выполнения полевых работ приступают к предварительной обработке триангуляции:
1. Проверяют полевые журналы и центрировочные листы.
2.Вычисляют средние значения направлений и составляют сводные ведомости измеренных величин.
3. Составляют схему сети с измеренными направлениями и углами.
4. Выполняют предварительное решение треугольников.
5. Вычисляют поправки за центрировку и редукцию.
6. Вычисляют приведенные к центрам направления.
7. Составляют схему сети с приведенными направлениями.
8. Вычисляют угловые невязки и проверяет их допустимость.
9. Делают оценку точности угловых измерений по невязкам треугольников.
10.Устанавливает допустимость невязок.
5. Виды условных уравнений в триангуляции.
При построении триангуляции в целях контроля и повышения точности кроме необходимых измеряют избыточные величины. Например, в треугольниках измеряют все три угла, хотя для их решения необходимо только два.
Геодезические сети, имеющие только необходимые исходные данные, называются свободными. Если сеть содержит избыточные исходные данные, то она несвободная. Каждое избыточное измерение и избыточное исходное данное позволяют записать математическое соотношение между измеренными величинами, т.е. условное уравнение.
При создании триангуляции возникают условия фигур, горизонтов, сумм, полюсов, сторон, дирекционных углов и координат.
1) Условие фигур, заключается в том, что в любой замкнутой фигуре сумма уравненных углов должна быть 1800(n–2).
Обозначим измеренные углы арабскими цифрами, поправки к ним – цифрами в скобках, уравненные значения углов – цифрами с чертой. Тогда условие фигуры треугольника ABO (рис. 2.9) запишется так
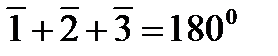 . (1)
. (1)
Учитывая, что 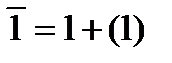 и т.д., получим
и т.д., получим
1+(1)+2+(2)+3+(3)–1800 = 0.
Обозначим
1+2+3–1800 = w.(2)
Тогда
(1)+(2)+(3)+w = 0. (3)
Полученное уравнение называется условным уравнением поправок. Здесь w – свободный член (невязка).
2) Условие горизонта заключается в том, что сумма уравненных углов, замыкающих горизонт на пункте, должна равняться 3600.

| Применительно к рис. 2.9 имеем
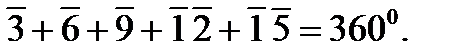 (4)
Выразив уравненные углы через измеренные и поправки к ним, получим условное уравнение поправок
(3)+(6)+(9)+(12)+(15)+wГ = 0, (5)
где wГ = 3+6+9+12+15–3600 – свободный член (невязка). (4)
Выразив уравненные углы через измеренные и поправки к ним, получим условное уравнение поправок
(3)+(6)+(9)+(12)+(15)+wГ = 0, (5)
где wГ = 3+6+9+12+15–3600 – свободный член (невязка).
|
| Рис. 2.9. |
3) Условие сумм заключается в том, что сумма, уравненных углов, входящих в исходный угол, должна равняться его значению. Условие возникает при построении типовой фигуры «вставка в угол».
Условие сумм для рис. 2.9 запишется так
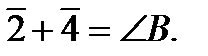 (6)
(6)
Условное уравнение поправок будет иметь вид
(2)+(4) +wS = 0, (7)
где
wS = 2+4 – 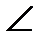 B. (8)
B. (8)
Условие сумм можно рассматривать и как условие дирекционных углов, так как угол B можно выразить через исходные дирекционные углы:
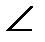 B = αBA – αBC. (9)
B = αBA – αBC. (9)
4) Полюсное условие заключается в том, что длина одной и той же стороны, вычисленная двумя независимыми путями по уравненным углам должна получить в обоих случаях одинаковое значение.
Возьмем в качестве исходной сторону ОА и вычислим дважды сторону ОD, решая треугольникипо часовой стрелке и против часовой стрелки. В результате получим
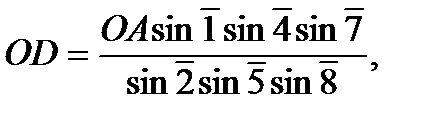 а)
а)
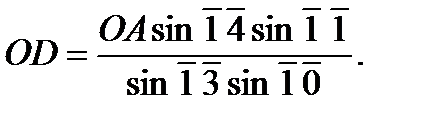 б)
б)
Разделив а) на б), получим условие полюса
 (10)
(10)
Равенство (10) можно получить, решая треугольники по ходу часовой стрелки, начиная от стороны OA и кончая стороной OA.
Если отношение синусов углов заменить отношением противоположных им сторон, получим очевидное равенство
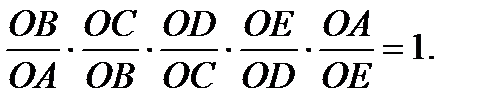
Все стороны имеют общую точку О, называемую полюсом.
Для перехода к условным уравнениям поправок в уравнении (10) необходимо заменить уравненные углы измеренными с поправками и привести его к линейному виду, разложив в ряд Тейлора, ограничиваясь первыми степенями поправок. В результате получим
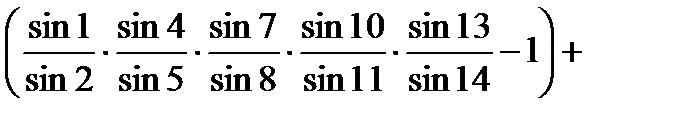
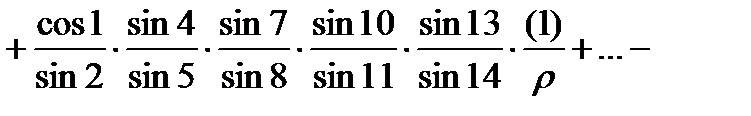
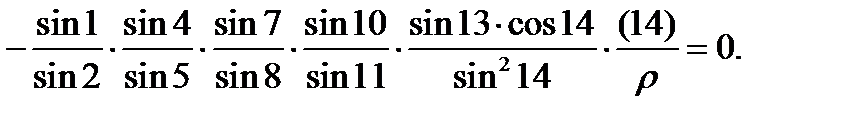
Если второе слагаемое умножить и разделить на sin1, то его с достаточной точностью можно заменить значением 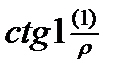 . аналогично можно преобразовать и другие слагаемые.
. аналогично можно преобразовать и другие слагаемые.
Умножим полученное выражение на ρ и введем следующие обозначения ctg i 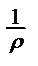 = δi,
= δi,
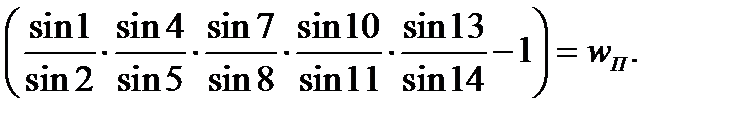
Тогда полюсное условное уравнение поправок в угловой мере будет иметь вид
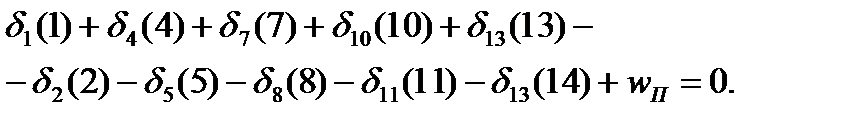 (11)
(11)
Если условиться обозначать связующие углы буквами А и В, как показано на рис. 2.10, то условие полюса можно записать короче:
 Рис. 2.10.
Рис. 2.10.
|
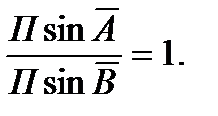 (12)
Условное уравнение поправок (12)
Условное уравнение поправок
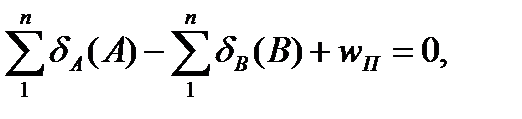 (13)
где (13)
где 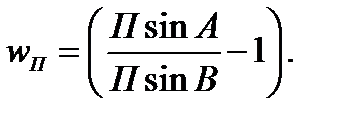
|
5) Условие сторон (базисов) заключается в том, что длина одной исходной стороны, вычисленная по другой исходной стороне и уравненным углам должна быть равна известному ее значению.

Рис. 2.11.
Для данной цепи треугольников, заключенной между исходными сторонами b1 и b2 можно записать
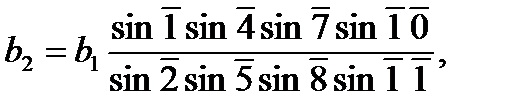
или в другом виде
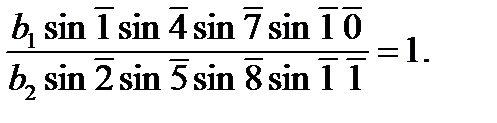 (14)
(14)
Это равенство и будет выражать условие сторон. Оно аналогично (10). Для перехода к условному уравнению поправок необходимо поступить так,как в предыдущем случае. В результате получим
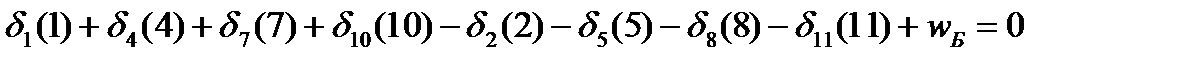 , (15)
, (15)
где
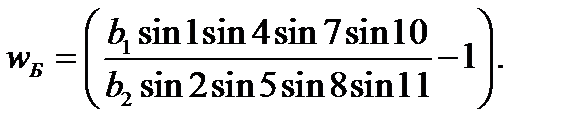 (16)
(16)
Если связующие углы числителя обозначить через А, а в знаменателе через В, то выражения (14), (15) и (16)можно записать короче:
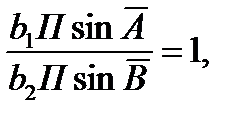 (17)
(17)
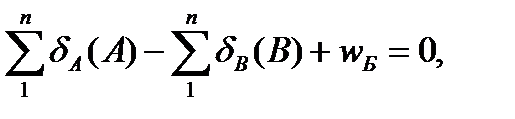
(18)
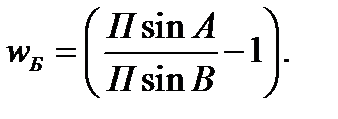 (19)
(19)
6) Условие дирекционных углов заключается в том, что дирекционный угол одной исходной стороны, вычисленный по дирекционному углу другой исходной стороны и уравненным углам должен быть равен известному его значению.
Для сети (рис. 2.11) условие записывается так
αСD = αAB+1800– 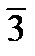 +
+ 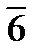 –1800+1800–
–1800+1800– 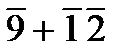 –1800.
–1800.
Заменим уравненные углы измеренными c поправками
αAB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]– αСD=0.
Обозначим
wα = αAB –3 + 6 – 9 + 12 – αСD. (20)
Тогда условное уравнение поправок примет вид:
–(3) + (6) – (9) + (12) + wα = 0. (21)
7) Условие координат заключается в том, что координаты исходной точки вычисленные по уравненнымуглам и координатам другой исходной точки должны быть равны известному значению. Условия абсцисс и ординат возникают тогда, когда в сети можно выделить ход, заключенный между двумя исходными пунктами.
В сети (рис. 2.11), например, можно наметить ход между точками В и С, показанный пунктиром.
Условные уравнения координат в сокращенном виде можно записать так
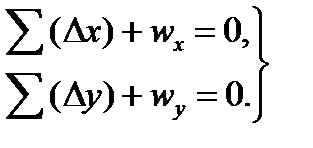 (22)
(22)
Здесь (Δх) и (Δу) – поправки в приращения координат, а wx и wy свободные члены (невязки), вычисляемые по формулам
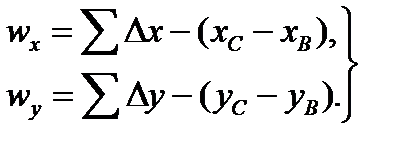 (23)
(23)
В окончательном виде поправки должны находиться к углам.
Общее число независимых условных уравнений в сети триангуляции и, в том числе по видам, определяется по схеме сети.
 Рис. 2.12.
Рис. 2.12.
| Для создания данной сети (рис.2.12) достаточно иметь два исходных пункта А и В и измерить 8 углов (1–8). Но в ней измерено 15 углов и сеть имеет избыточные исходные данные (координаты точки С). Общее число избыточных исходных данных составит 15–8+2=9. Следовательно, в сети возникает 9 независимых условных уравнений: 5 условий фигур, условие горизонта, сумм, полюса, и сторон. |
Условные уравнения поправок будут иметь вид:
1. (1) + (2) + (11) + w1 = 0.
2. (3) + (4) + (12) + w2 = 0.
3. (5) + (6) + (13) + w3 = 0.
4. (7) + (8) + (14) + w4 = 0.
5. (9) + (10) + (15) + w5 = 0.
6. (11) + (12) + (13) + (14) +(15) + wГ = 0.
7. (2) + (3) + wS = 0.
8. δ1(1)–δ2(2)+δ3(3)–δ4(4)+δ5(5)–δ6(6)+δ7(7)–δ8(8)+δ9(9)–δ10(10)+ wП = 0.
9. δ1(1)–δ11(11)+δ12(12)–δ4(4)+ wБ = 0.
Свободные члены найдутся по формулам:
w1 = 1 + 2 + 11 – 1800,
… … …
wГ = 11 + 12 + 13 + 14 + 15 – 3600,
wS = 2 + 3 – В,
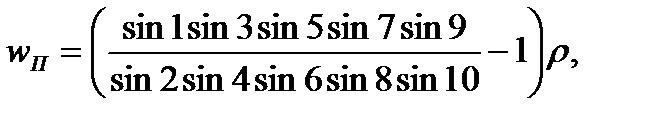

Рассмотренные выше условные уравнения справедливы при уравнивании углов. Если уравниваются направления, то вместо поправок угла записывают разность поправок в направления.
Соответствующие виды условных уравнений через поправки в направления приведены в учебном пособии [40].
Дата добавления: 2015-08-26; просмотров: 2715;
