Основы теории проекции Меркатора

Меркаторская проекция относится к классу цилиндрических, нормальных, равноугольных проекций, в которых картографическая сетка представляет собой взаимно перпендикулярные параллели и меридианы. Расстояние между меридианами соответствует разности долгот. Цилиндрическая проекция задается уравнениями:

x = f(j) и y = c*l,

где х и у - картографические координаты в прямоугольной системе.

Первое уравнение параллелей, а второе меридианов. Термин цилиндрическая говорит о том, что проекция эллипсоида или шара выполняется на поверхность цилиндра. Меркаторская проекция не может быть представлена четкой геометрической картиной из-за налагаемого на нее требования равноугольности.

Этапы проектирования морской навигационной карты:

• Первый этап. Геодезические измерения на поверхности Земли и координатные привязки к референц-эллипсоиду.
• Второй этап. Уменьшение размеров референц-эллипсоида до определенного масштаба с целью развертывания его на плоскость. Это математическое преобразование эллипсоид – глобус сохраняет геометрическое подобие контуров изображений. Масштаб преобразований называется главным масштабом карты (m₀).
• Третий этап. Выбор картографической проекции развертывания глобуса на плоскость и преобразование глобус – карта. При проектировании эллипсоида на плоскость масштаб m₀ будет постоянным на ограниченном множестве точек карты. При удалении этого множества, масштаб изменяется и становится частным (m) другого множества точек. Отношение с = называется увеличением масштаба.

Если с = а, где а – радиус экватора, то масштаб вдоль экватора n₀ равен главному масштабу m₀ и в этом случае говорят, что проекция будет на касательный цилиндр. Если масштаб выбран вдоль какой-либо параллели и он равен главному масштабу m₀ , то говорят о проекции на секущий цилиндр.

На рисунке 1.51 а) дана элементарная трапеция поверхности земного эллипсоида в масштабе m₀ и ограниченная отрезками параллелей и меридианов. Локсодромией является диагональ трапеции и имеет элементарную длину ds.

На рисунке 1.51 b) желаемая форма этой трапеции после применения к ней математического преобразования, называемого картографической проекцией.

а) b)

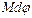ds dx ds Рис. 1.51

NCosj dl dy = c dl

В этой трапеции масштабы преобразования эллипсоид – глобус по параллели n и меридиану m равны m = n = m₀, откуда углы на глобусе равны углам на эллипсоиде.

При проектировании глобуса на плоскость нужно сохранить равенство углов, при этом изменится конфигурация координатной сетки, но отношение 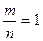остается постоянным.

Сравним длину меридиана на трапеции и четырехугольнике:

, ,

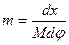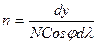Поскольку у = а l, так как на экваторе с = а и dy = a dl, то n = .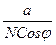

Приравняем масштабы m и n:

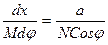, отсюда dx = 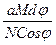. Проинтегрируем полученное выражение по х и по j.

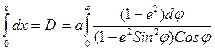. (1.69)

Это есть закон изменения расстояния от экватора по меридиану до параллели места наблюдателя.

Окончательно запишем уравнение меркаторской проекции и формулу масштабов после интегрирования.

x = D = a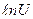

y = a l

m = n = .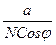

Величина U в математической картографии называется изометрической широтой.

Для шара уравнения преобразуются:

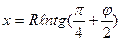
y = R l

m = n = 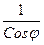, где

R – радиус шара.

Размерность х и у выражается в метрах, для целей навигации удобней их выразить в экваториальных минутах. Радиус экватора в минутах дуги а = 3437,74¢ , тогда

х = D = 3437,74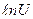

Для перехода от натуральных к десятичным логарифмам применим коэффициент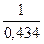

Тогда, произведя преобразования, получим:

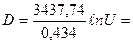7915,704468 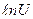(1.70)

Для шара это будет D = 7915,704468 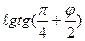(1.71)

Величина x или D, или МЧ называется меридиональной частью и представляет собой расстояние, отсчитываемое на меркаторской карте по меридиану от экватора до данной параллели, и выражается в минутах (милях) дуги экватора. Значение МЧ приведено в картографических таблицах и в МТ (табл. 26 МТ-63).

Анализируя последнее выражение, находим существенное ограничение карты в меркаторской проекции. Если j = 90°, то D = ¥, т.е. на карте в меркаторской проекции предполюсное и полюсное пространство изобразить не возможно.

О главном масштабе навигационной карты.

Главный масштаб карты показывает во сколько раз уменьшено изображение земной поверхности вдоль конкретной параллели при ее проектировании на карту. Численно это будет выглядеть как отношени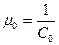е: , где

С₀ – знаменатель главного масштаба. Он всегда приводится в заголовке карты. Для оптимальной стыковки карт главные параллели определяют для каждого моря и карты данного бассейна имеют одну главную параллель. Для Балтики j₀ = 60N, для Белого моря j₀ = 66°N, для Черного моря j₀ = 44°, для открытых частей мирового океана j₀ =0°, j₀ = 25° (N,S) и j₀ = 40° (N,S).

На карте различают главный масштаб и частный масштаб. Частный масштаб сохраняется постоянным вдоль параллели и изменяется при переходе от одной параллели к другой. Частный масштаб по мере удаления от главной параллели к полюсам (N, S) увеличивается, а к экватору уменьшается. Для перехода от масштаба главной параллели к частному масштабу используют формулу 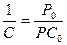, где 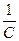- частный масштаб карты, 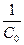- масштаб по главной параллели,

Р₀ – длина одной минуты (1¢^¢) дуги главной параллели (мм).

Рассмотрим Рис. 1.51 (a, b) для вывода отношений масштабов на параллели к масштабу на экваторе. Как было выяснено, масштабы m и n являются функцией географической широты.

Из рисунка (Рис.1.52) выявляем равенство АВ = È а в = R arc 1¢.

Длина отрезка АВ на проекции выразится отношением:

е = 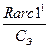(1.72)

Величина е - это изображение 1 экваториальной мили, выраженная в линейных мерах (миллиметрах), называется единицей карты.

Длина отрезков А¹ В¹ и А² и В² можно выразить по подобию отрезка экватора АВ, как:

А¹ В¹ = а¹ в¹ = R Cosj₁ arc1¹

A² B² = a² в² = R Cosj₂ arc1¹

Тогда единица карты е определится отношениями:

С₁ и С₂ – знаменатели численного масштаба на соответствующей параллели j₁ и j₂.

Параллель в широтах j₁ и j₂ считается главной параллелью. Если взять отношения численного масштаба на экваторе к численным масштабам на параллелях, то получим, что их отношения зависят от Secj_i.

a) b)

Р_N

RCosj² о²

а² в² А² В²

RCosj¹ о¹

а¹ А¹ В¹

в¹

j¹ R j² о Рис. 1.52

а R

в А В

е =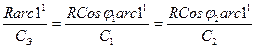

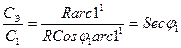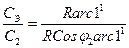, = Secj₂

отсюда вытекает, что знаменатель численного масштаба на меркаторской карте, считаемый вдоль экватора в Secj раз больше знаменателя численного масштаба главной параллели в широте j.

Если перейти от формы Земли в виде шара к форме сфероида, то взаимосвязь численных масштабов между собой и единицы карты от численного масштаба на экваторе перепишутся в виде:

С_Э = С₁ SecU₁ = C₂SecU₂ (1.73)

e = 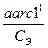(1.74)