Средние структурные величины
В условиях недостаточности средних используют структурные средние величины – моду и медиану.
Медиана (Ме) – это вариант, который находится а середине вариационного ряда. Медиана делит ряд на две равные (по числу наблюдений) части. В ранжированных рядах не сгруппированных данных нахождение медианы сводится к отысканию порядкового номера и значения варианта у этого номера.
Медиана в интервальныхвариационных рядах рассчитывается по формуле:
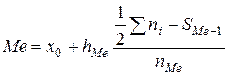 , (1.17)
, (1.17)
где х0 – нижняя граница медианного интервала (накопленная частота которого превышает половину общей суммы частот);
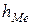 – величина медианного интервала;
– величина медианного интервала;
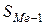 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
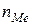 – частота медианного интервала.
– частота медианного интервала.
Также в интервальных вариационных рядах медиана может быть найдена с помощью кумуляты как значение признака, для которого
 или
или  . (1.18)
. (1.18)
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины: 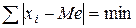 .
.
Модой(Мо) вариационного ряда называется вариант, которому соответствует наибольшая частота.
Для вычисления моды в интервальном ряду сначала находится модальный интервал, имеющий наибольшую частоту (или наибольшую плотность распределения – отношение частоты интервала к его величине ni/hi – в интервальном ряду с неравными интервалами), а значение моды определяется линейной интерполяцией:
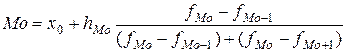 , (1.19)
, (1.19)
где хо – нижняя граница модального интервала;
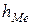 – величина модального интервала;
– величина модального интервала;
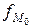 ,
, 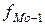 ,
, 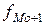 – частота ni (в интервальном ряду с равными интервалами) или плотность распределения ni/hi (в интервальном ряду с неравными интервалами) модального, до и послемодального интервала.
– частота ni (в интервальном ряду с равными интервалами) или плотность распределения ni/hi (в интервальном ряду с неравными интервалами) модального, до и послемодального интервала.
Мода так же, как и медиана обладает определенной устойчивостью к вариации признака. Если в совокупности первичных признаков нет повторяющихся значений, то для определения моды проводят группировку.
Графически отобразить моду по гистограмме можно следующим образом: нужно взять столбец, имеющий наибольшую высоту, и из его левого верхнего угла провести отрезок в угол последующего столбца, а из правого угла – в верхний правый угол предыдущего столбца, абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности. Медиану приближенно можно определить графически - по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения и есть медиана (рисунок 1.1)
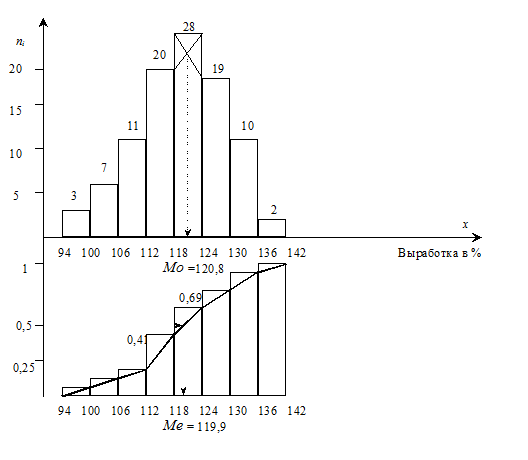 |
Рис. 1.1 Графическое отображение интервального вариационного ряда
В симметричных рядах имеет место следующее соотношение моды, медианы и средней арифметической 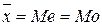 (1.20).
(1.20).
В случае, если 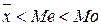 (1.21), имеет место левосторонняя асимметрия ряда.
(1.21), имеет место левосторонняя асимметрия ряда.
В случае, если  (1.22), имеет место правосторонняя асимметрия ряда.
(1.22), имеет место правосторонняя асимметрия ряда.
Мода и медиана,в отличие от степенных средних, являются конкретными характеристиками ряда. Медиана – характеризует центр, вычисляется проще и не чувствительна к концам интервала. Мода – наиболее вероятное значение в изучаемой совокупности (например, наиболее возможные результаты).
 1 2 3
1 2 3
1 – распределение с левосторонней асимметрией
2 – распределение с правосторонней асимметрией
3 – нормальное (симметричное) распределение
Дата добавления: 2015-08-26; просмотров: 1029;
