Показатели вариации. Вариациейназывается изменяемость, колеблемость величины признака
Вариациейназывается изменяемость, колеблемость величины признака. Вариация проявляется в отклонениях от средних и зависит от множества факторов, влияющих на социально-экономическое явление. Вариация бывает случайной и систематической, существует в пространстве и во времени. Показатели вариации делятся на абсолютные и относительные (таблица 2.1).
Таблица 2.1 - Показатели вариации
| Показатель | Формула расчета показателя | |
| простой | взвешенный | |
| Абсолютные | Размах | 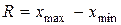 (2.1) (2.1)
|
| Среднее линейное отклонение | 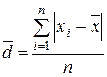 (2.2) (2.2)
|  * (2.3) * (2.3)
|
| Дисперсия | σ2 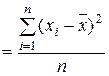 (2.4) (2.4)
| 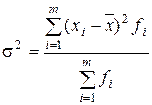 (2.5) (2.5)
|
| Среднее квадратическое отклонение | 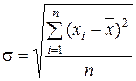 (2.6) (2.6)
| 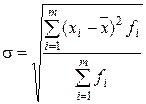 (2.7) (2.7)
|
| относительные | Коэффициент вариации |  (2.8) (2.8)
|
| Линейный коэффициент вариации | 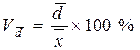 (2.9) (2.9)
| |
| Коэффициент осцилляции | 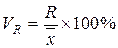 (2.10) (2.10)
|
*– Здесь fi – частота ( 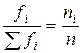 ).
).
Относительные показатели (коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции) строятся с учетом базы (в виде средней), выражаются в процентах и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации
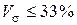 . (2.11)
. (2.11)
Для расчета дисперсии можно использовать модифицированную формулу:
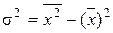 . (2.12)
. (2.12)
Выведем эту формулу из формулы (2.5)
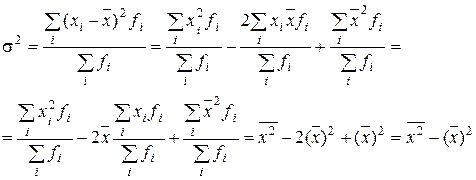
Для расчета дисперсии можно использовать способ отсчета от условного нуля, который позволяет упростить вычисления при больших значениях признака. Тогда дисперсия вычисляется по формуле:
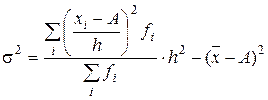 , (2.13)
, (2.13)
где h – величина интервала;
А – условный нуль, в качестве которого можно использовать как середину серединного интервала, так и середину интервала с наибольшей частотой.
Дата добавления: 2015-08-26; просмотров: 800;
