Правило сложения дисперсий
Дисперсия, в отличие от других характеристик вариации, является аддитивной величиной. То есть в структурированной совокупности, которая поделена на группы по факторному признаку, дисперсия результативного признака может быть разложена на: дисперсию в каждой группе (внутригрупповую) и дисперсию между группами (межгруповую). Общая дисперсия характеризует вариацию признака за счет влияния всех причин (факторов), межгрупповая – за счет фактора, положенного в основу группировки, а внутригрупповые - за счет других факторов, не учтенных в группировке.
Межгрупповая дисперсия вычисляется по формуле
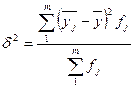 ,
,
где: 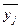 и
и 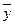 – соответственно средняя j-й группы и общая средняя варьирующего признака y;
– соответственно средняя j-й группы и общая средняя варьирующего признака y; 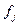 – частота j-й группы.
– частота j-й группы.
Внутригрупповая дисперсия рассчитывается отдельно для каждой j-й группы:
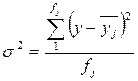 ,
,
где y – значения признака отдельных элементов совокупности.
Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующей группы:
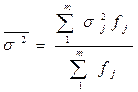 .
.
Взаимосвязь между тремя дисперсиями называется правилом сложения дисперсий, согласно которому
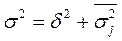 .
.
Общую дисперсию можно определить и по формуле
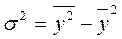 .
.
Отношение межгрупповой дисперсии к общей называется корелляционным отношением η².η2 = δ2 / σ2 < 1
Приклад. Розрахунок зазначених дисперсій показано за даними табл. 4.5, на прикладі урожайності винограду.
Варіація урожайності окремо для кожного сорту винограду визначається трьома внутрішньогруповими дисперсіями. Для сорту винограду „Аліготе” внутрішньогрупова дисперсія становить
 ,
,
де 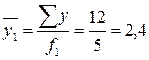 .
.
Таблиця 4.5
| Сорт винограду | Кількість кущів, 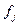
| Урожайність з одного куща, кг
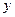
| 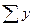
| 
|
| Аліготе | 2,3; 2,2; 2,7; 2,6; 2,2 | 2,4 | ||
| Фетяска | 2,9; 3,3; 2,7; 2,8; 3,2; 3,4; 2,8; 2,9 | 3,0 | ||
| Рислінг | 3,6; 4,0; 4,1; 4,4; 3,8; 3,9; 4,2 | 4,0 | ||
| В цілому | Х | 3,2 |
Аналогічно обчислено внутрішньогрупові дисперсії для другої та третьої груп: 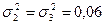 .
.
Середня з групових дисперсій дорівнює
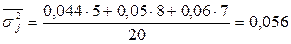 ,
,
Міжгрупова дисперсія становить
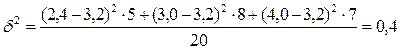 , де
, де 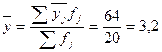 .
.
Загальну дисперсію урожайності визначимо за правилом складання дисперсій як суму міжгрупової та середньої з групових дисперсій:
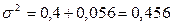 .
.
Безпосереднє обчислення загальної дисперсії за спрощеною формулою
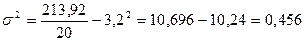
дає такий самий результат.
5.4. Графічне зображення рядів розподілу
Для зображення варіаційного ряду використовують такі графіки: полігон, гістограму, кумуляту, огіву,тощо.
Полігон — це графічне зображення варіаційного ряду в прямокутній системі координат, коли ознака відкладається на осі абсцис, а частоти або частки (щільність розподілу) — на осі ординат.
Частіше за все полігон застосовують для зображення дискретного варіаційного ряду, однак його можна використовувати і для інтервального ряду.
Проілюструємо графічно ряди розподілу
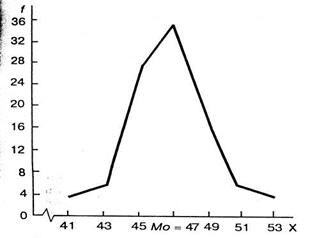
|
За допомогою полігона можна визначити також моду, для цього з його вершини опускають перпендикуляр на вісь абсцис, а точка їхнього перетину і є модою. У наведеному прикладі мода відповідає врожайності 47 центнерів з гекгара озимої пшениці.
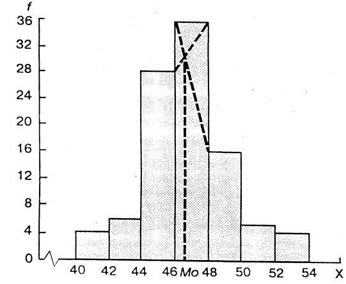
Гістрограма — це графічне зображення інтервального варіаційного ряду. На осі абсцис відкладають ознаки (варіанти). Утворені прямокутники пропорційні за висотою частотам значень ознаки для кожного інтервалу. В разі нерівних інтервалів висота прямокутників має бути пропорційною щільності розподілу ознаки у відповідному інтервалі.
Для графічного визначення моди за допомогою гістограми штриховими лініями сполучають верхні куги модального інтервалу і стовпчиків, що прилягають до нього. Модою є перетин осі абсцис перпендикуляром, опущеним з точки зіткнення цих прямих, як показано на рис. 1.5. Цей метод коректніше оцінює модальне значення, оскільки він враховує передмодальну і післямодальну частоти, тобто за гістограмою мода дорівнює 46,67 центнера з гектара. Графічне визначення моди можливе тільки у варіаційних рядках розподілу з рівними інтервалами.
Кумулятивні діаграми (кумуляти) використовують для графічного порівняння двох або більше варіаційних розподілів з рівними чи нерівними інтервалами. Для їх побудови використовують прямокутну систему координат, де на осі абсцис відкладають відрізки інтервалів групувань, а на осі ординат — нагромаджені частоти або частки. Висота прямокутників відповідає кумулятивним частотам або часткам певних інтервалів ряду розподілу. При побудові кумуляти інтервальної ознаки нижній межі першого інтервалу відповідає частота, яка дорівнює нулю, а верхній — частота першого інтервалу. Вершій межі другого і наступних інтервалів відповідають їхні нагромаджені частоти, а останнього інтервалу—сума всіх частот
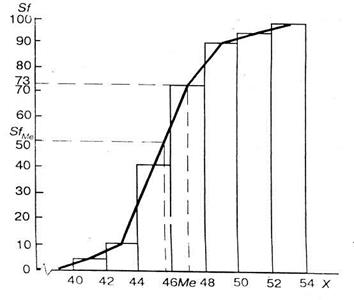
Кумулятивна гісторама розподілу господарств регіону за врожайністю озимоїпшениці
На підставі кумулятивної кривої розподілу визначають скільки одиниць сукупності, або яка частка не перевищує певного значення групувальної ознаки. На рис. 8.8 штрихові лінії вказують на те що зі 100 господарств регіону 73 мали врожайність озимої пшениці менш ніж 47 центнерів з гектара.
Графічне визначення медіани: з точки на осі ординат яка відповідає півсумі нагромаджених частот SfМе, проводять штрихову лінію (рис. 1.8), паралельну осі абсцис. Перпендикуляр, опущений точки перетину цієі прямої з кумулятою на вісь абсцис укаже на медіану. В нашому прикладі Me = 45,5 центнера з гектара
При побудові кумуляти дискретної ознаки на осі абсцис відкладають значення варіантів, а на осі ординат - нагромаджені підсумки частот або часток. Сполучивши вершини ординат прямими лініями, дістанемо кумулятивну криву, яку ще називають кумулятивним полігоном.
Різновидом кумулятивного розподілу варіаційного ряду є огіва. Вона є дзеркальним відображенням кумуляти розподілу. При її побуві на осі абсцис відкладають нагромаджені частоти або частки, а на ординат — межі інтервалів варіаційного ряду розподілу.
Задача. Представлено распределение радиаторов по времени их паяния
| Время паяния, мин | Кол-во радиаторов | Хi | Xi fi | Хі-Х | ΙХі-ХΙfi | (Хі-Х)²fi | Sfi |
| fi,шт. | |||||||
| 20 - 30 | |||||||
| 30 - 40 | |||||||
| 40 - 50 | |||||||
| 50 - 60 | |||||||
| 60 - 70 | |||||||
| Всего |
Показатели центра распределения:
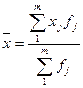 =
=
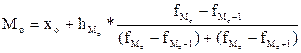 =
=
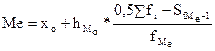 =
=
Показатели вариации:
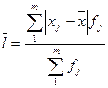 =
=
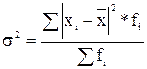 =
=
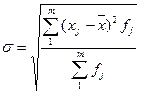 .=
.=
Линейный коэффициент вариации 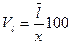 % =
% =
Квадратический коэффициент вариации 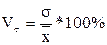 =
=
Показатели формы распределения:
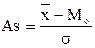 =
=
Выводы
Дата добавления: 2015-08-26; просмотров: 1458;
