Сущность и виды рядов распределения
Сущность и виды рядов распределения
Статистические характеристики рядов распределения
Правило сложения дисперсий
Графическое изображение рядов распределения
Сущность и виды рядов распределения
Ряд распределения характеризует состав, структуру совокупности по определенному признаку. Элементами ряда распределения являются варианты – значения признака xj и частоты fj. В зависимости от статистической природы вариант ряды делятся на атрибутивные ивариационные. В соотношении вариант и частот проявляется закономерность распределения.
Построение рядов распределения выплывает из принципов статистического группирования. Известно, что ряды распределения можно образовать или по атрибутивным, или по количественным (вариационным) признакам.
При построении атрибутивных рядов распределения варианты нужно расположить в логической последовательности. В случае использования дискретных и интервальных вариационных рядов варианты записывают по возрастанию или убыванию. Для интервальных рядов важно четко разграничивать варианты.
Различают ряды распределения с абсолютными, относительными и накопленными частотами. Накопленные частоты называют кумулятивными. В первом случае частоты являются абсолютными числами, во втором — удельным весом или частью каждой группы. Ряды распределения с абсолютными частотами характеризуют состав совокупности, а с относительными — их структуру. Ряды распределения с накопленными (кумулятивными) частотами указывают на количество или удельный вес единиц со значением признака, меньшим от заданного. Кумулятивные частоты находятся суммированием их по группам.
5.2. Статистические характеристики рядов распределения:
1) частотные;
2) характеристики центра распределения;
3) характеристики вариации;
4) характеристики неравномерности распределения.
1) Частотные характеристики– это абсолютная численность і-й группы, то есть частота fi, и относительная частота, то есть доля di
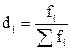
Если интервалы вариационного ряда неравные, то рассматривают плотность частоты
gi=fi/hi и плотность доли gi=di/hi Плотность распределения — это количество единиц совокупности, приходящееся на единицу величины интервала группировального признака 
 .
.
Дополнительной характеристикой вариационных рядов является кумулятивная частота Sf 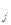 (доля Sd
(доля Sd 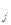 ), характеризующая объем совокупности со значением варианты, которые не превышают xj. Кумулятивные частотные характеристики образуются последовательным суммированием абсолютных или относительных частот. Так,
), характеризующая объем совокупности со значением варианты, которые не превышают xj. Кумулятивные частотные характеристики образуются последовательным суммированием абсолютных или относительных частот. Так, 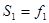 ,
, 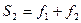 ,
, 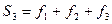 и т.д.
и т.д.
2) К характеристикам центра распределения относят среднюю, моду и медиану.
Середняя величина характеризует типичный уровень признака в совокупности. По данным ряда распределения средняя рассчитывается как арифметическая взвешенная:
на основе частот на основе долей
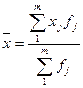 ;
; 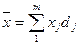 ,
,
где m – число груп.
Мода –это варианта, имеющая наибольшую частоту, то есть значение признака, наиболее часто встречающееся в совокупности. В дискретном ряду (определяется визуально). Если моды две – то это бимодальный вариационный ряд
36,37,37,38,37,38,39,40 Мо=37
В интервальном ряду распределения сначала определяется модальный интервал, а уже в пределах этого интервала – точное значение моды.
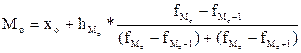
(где хо – нижня граница модального интервала; hMo – ширина модального интервала;
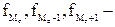 частота модального, предмодального и послемодального
частота модального, предмодального и послемодального
интервалов соответственно)
Медиана –значение признака, являющееся серединой вариационного ряда, то есть делящее его на две равные части.
36,37,37,37|38,38,39,40
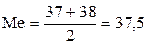
В интервальном ряду распределения сначала определяется медианный интервал, а уже в пределах этого интервала – точное значение медианы:
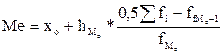
де хо – нижня граница медианного интервала;
hMo – ширина медианного интервала;  – частота медианного интервала;
– частота медианного интервала;
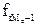 – кумулятивная частота предмедианного интервала)
– кумулятивная частота предмедианного интервала)
В одномодальных симметричных рядах распределения 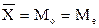
Дата добавления: 2015-08-26; просмотров: 1575;
