Характеристики вариации
Для измерения и оценки вариации используют абсолютные характеристики (вариационный размах, среднее линейное отклонение, среднеквадратическое отклонение) и относительные характеристики (коэффициенты вариации, неравномерности распределения).
а)абсолютные характеристики вариации:
Вариационный размаххарактеризует диапазон вариации, это разница между максимальным и минимальным значениями признака.
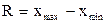
Середнее линейное отклонение– это середнее из модулей отклонений индивидуальных значений от центра распределения
;
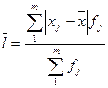Дисперсия– это средний квадрат отклонений индивидуальных значений признака от центра распределения
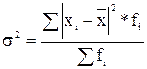
Середнее квадратическое отклонение –это корень квадратный из дисперсии
; 
.
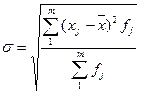По первичным, несгруппированным данным эти характеристики вариации рассчитываются по принципу простой средней, то есть:
; 
.
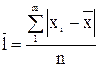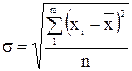Середнее квадратическое отклонение и среднее линейное отклонение по смыслу идентичны, но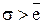 
.
Для альтернативного признака, вариация которого имеет два значения „да” и „нет”. дисперсия рассчитывается по формуле, как произведение долей:
б)относительные характеристики вариации:
Сравнивая вариации разных признаков или одного признака в разных совокупностях используют относительные характеристики вариации. Коэфффициенты вариации рассчитываются как отношения абсолютных, именованных характеристик вариации (σ, 
, R) к центру распределения и часто выражаются процентами, то есть:
Линейный коэффициент вариации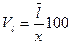 
Квадратический коэффициент вариации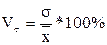 
Коэффициент осцилляцииї 
Чем менье среднее отклонение, тем более типична средняя, тем более однородна совокупность. Квадратический коэффициент вариации используют как критерий однородности совокупности. В симметричном, близком к нормальному, распределении Vs = 0,33.
Если: V < 10% - незначительная вариация, совокупность однородна;
10 % ≤ V ≤ 30% - середнее колебание, совокупность в пределах однородности, значение средней можна считать типичным уровнем признака в данной совокупности;
V > 33% - високий уровень вариации, совокупность неоднородна, значение средней нельзя считать типичным уровнем признака в данной совокупности.
4)характеристики неравномерности распределения:
Наиболее простой мерой асимметричности распределения является отклонение между характеристиками центра распределения. Так как в симметричном распределении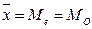 
, то чем заметнее асимметрия, тем больше отклонение 
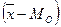. Стандартное отклонение называют коэффициентом асимметрии
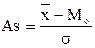
При правосторонней асимметрии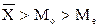 
, и Аs>0. При левосторонней асимметрии 
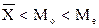, a As<0.
Дата добавления: 2015-08-26; просмотров: 750;