Композиція відображень

Нехай задано два відображення: f : X → Y та g: Y → Z. Тоді композицією відображень f і g (позначаємо символом g ○ f) будемо називати відображення з множини X в множину Z, визначене виразом g ○ f (x) = g(f (x)) для всіх елементів x з множини X. Прийняте правило, згідно з яким у композиції g ○ f треба починати з відображення f, розташованого праворуч.

Наприклад, нехай маємо множини Х = {l, 2, 3, 4}, Y = {а, b, c}, Z = {u, v}та два відображення

f : Х → Y, 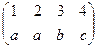, g : Y → Z,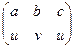

Тоді композиція заданих відображень g ○ f: Х → Z,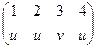

Композиція відображень асоціативна, тобто якщо маємо три відображення f : X → Y, g: Y → Z, h: Z → U, то (h ○ g) ○ f = h ○ (g ○ f) = h ○ g ○ f.

Відображення g: Y → X називається оберненим до відображення f : X → Y, якщо виконуються такі умови f ^-1 ○ f = I_X (I_X - тотожне відображення на множині X), f ○ f ^-1 = I_Y (I_Y - тотожне відображення на множині Y).

Для відображення f існує обернене відображення f ^-1 тоді і тільки тоді, коли відображення f бієктивне. Обернене відображення f ^-1 також є бієктивним.

Якщо f :X → Y - бієкція й g: Y → Z - бієкція, то g ○ f - бієкція з Х в Z, а її обернена бієкція дорівнює f ^-1 ○ g ^-1.

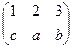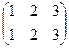Наприклад, нехай задані множини Х ={l, 2, 3}, Y = {а, b, c} та відображення f : Х → Y, . Це відображення є бієктивним, і тому до нього існує обернене f ^-1: Y → X, . Дійсно, f ^-1 ○ f = = I_X та f ○ f ^-1 = 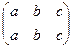= I_Y.