Построение полной таблицы смертности
Построение таблиц смертности является в принципе несложной, но достаточно трудоемкой вычислительной процедурой. Она включает в себя несколько этапов3:
· расчет значений исходного показателя для всех возрастов на основе данных статистики смертности (распределения умерших по возрастам);
· если необходимо, обработку этого ряда значений для уст
ранения искажений, вызванных возрастной аккумуляцией;
· интерполяцию ряда значений для устранения возможных
пропусков или экстраполяцию для расчета значений для самых
старших возрастов;
· вычисление остальных функций таблицы смертности.
Основная методическая проблема построения таблиц смертности, как уже говорилось, связана с переходом от реальных показателей повозрастной смертности к табличным вероятностям умереть в данном возрасте, т.е. от тх* к qx.
Методы построения таблиц смертности занимают большое место в демографии. Можно повторить уже сказанное выше, что история демографии в значительной мере совпадает с историей разработки и совершенствования этих методов.
Современные таблицы смертности рассчитываются с помощью т.н. косвенного, или демографического, метода. Демографический метод назван так потому, что в его основе лежат данные о повозрастной смертности, а также о возрастно-половой структуре населения, получаемые во время переписей и текущего учета. Косвенным этот метод назван, чтобы противопоставить его т.н. прямому методу, или, иначе, методу Р. Бека, основанному на непосредственном расчете показателей таблицы смертности в ситуации, когда известно распределение смертей на элементарные совокупности сетки Лексиса4.
Исходным показателем здесь служит повозрастной коэффициент смертности, который приравнивается к табличному
коэффициенту смертности (dx/Lx) и на основе которого определяются все функции таблицы смертности, начиная, разумеется, с вероятности умереть в возрасте х лет. Демографический метод позволяет строить таблицы смертности, наиболее адекватно отражающие ее уровень. При этом на величину итоговых показателей не влияют колебания чисел родившихся и умерших в годы, предшествовавшие расчету5.
Проблема, связанная с переходом от повозрастных коэффициентов смертности к вероятностям смерти на возрастном интервале (х, х+п) лет, состоит в том, что первые, как известно, рассчитываются по отношению к общему числу человеко-лет, прожитых населением на этом возрастном интервале, или к его приближению, т.е. среднегодовому населению. Вторые же рассчитываются по отношению к численности населения в начале возрастного интервала. Чтобы построить таблицу смертности, надо установить соотношение между ними, т.е. между тх и qx. Иначе говоря, нужно перейти от тх к qx6.
Пусть Nx - число доживающих до возраста х лет в реальном населении. Из этого числа до следующего возраста х+1 лет не доживет Dx. Тогда, по определению:
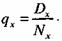
·
Вместе с тем повозрастной коэффициент смертности тх равен отношению Dx к числу человеко-лет, прожитых Nx в течение интервала (х, х + 1). Это число человеко-лет, в свою очередь, равно сумме двух слагаемых:
Первое слагаемое - это (Nx - Dx, т.е. число человеко-лет, прожитых на этом интервале возраста теми, кто дожил до возраста (х, х + 1).
Второе слагаемое - это число человеко-лет, прожитых на этом интервале возраста теми, кто не дожил до возраста (х, х + 1), т.е. умер на этом интервале возраста. Это число равно a'x-Dx.
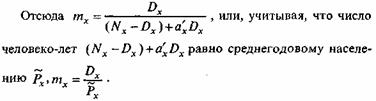
Последнее выражение есть знакомая формула расчета повозрастного коэффициента смертности.
Решим уравнение Рх = (NX -Dx) + a'xDx относительно Nx:
Nx=Px+(1-a'xDx). Подставим это выражение в приведенную выше формулу для qx.
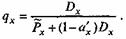
Если числитель и знаменатель этого выражения разделить на Рx , то получим искомое базисное соотношение между qx и тх:

Величины а0 а1 ...варьируют от страны к стране в зависимости от уровня смертности. Для развивающихся стран, в которых смертность высока, обычно принимается а0 - 0,3, a1 - 0,4 и 0,5 для всех остальных. Там же, где смертность низка, наилучшей величиной для а0 является 0,1. В целом выбранная величина не является критичной, за исключением а0. Более того, существует альтернативный путь определения q0 без использования вышеприведенной формулы. Речь идет о простом приравнивании q0 к коэффициенту младенческой смертности. Newell С. Methods and Models in Demography. London. 1988. P. 69.
Приведенное выше уравнение является фундаментальным для построения современных таблиц смертности. Зная все qx и выбрав корень таблицы смертности l0 , можно, используя приведенные выше соотношения между ними, построить все остальные функции таблиц смертности.
Дата добавления: 2015-07-14; просмотров: 854;
