Основне рівняння гідростатики. Якщо на рідину, що перебуває у нерухомій судині, діє лише сила ваги, то такий стан рідини називають абсолютним спокоєм (відносно Землі)
Якщо на рідину, що перебуває у нерухомій судині, діє лише сила ваги, то такий стан рідини називають абсолютним спокоєм (відносно Землі). Нехай рідина перебуває в судині й на неї діє тільки сила тяжіння (рис. 8). Тиск на поверхню рідини позначимо через Р0. При дії на рідину тільки сил ваги (стан абсолютного спокою) будемо мати: Х = 0, Y = 0, Z = -g. Підставивши ці значення у рівняння (1.32), отримаємо:
dР = - rgdz
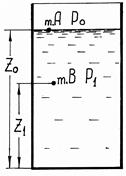 Рис.8. До виведення основного рівняння гідростатики.
Рис.8. До виведення основного рівняння гідростатики.
| У результаті інтегрування цього рівняння для нестисливої рідини одержимо:
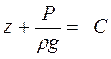 . (1.33)
Для знаходження сталої інтегрування С візьмемо на поверхні рідини точку А , для якої z = z0, а Р = Р0. Тоді (1.31) можна подати так: . (1.33)
Для знаходження сталої інтегрування С візьмемо на поверхні рідини точку А , для якої z = z0, а Р = Р0. Тоді (1.31) можна подати так:
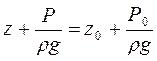 . (1.34) . (1.34)
|
Рівняння (1.34) називають основним рівнянням гідростатики.
Це рівняння для точки В записується у вигляді:
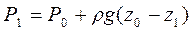 (1.35)
(1.35)
і називається законом Паскаля, який читається так:
Тиск, який утворюється в будь-якій точці рідини, що покоїться, передається однаково усім точкам її об’єму, або при будь-якій зміні тиску Р1 тиск Р2 в іншій точці рідині змінюється на стільки ж.
1.2.3. Деякі практичні застосування основних рівнянь гідростатики
1) Принцип посудин, що сполучаються.
Якщо судини, що сполучаються, заповнені двома рідинами, які не змішуються, і мають густини r1 і r2, то при проведені площини порівняння крізь границю поділу рідин, отримаємо
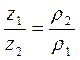 . (1.36)
. (1.36)
2) Пневматичний вимір рівню рідини в резервуарі (рис. 9).
Припустимо, що є судина з рідиною, рівень якої недоступний для виміру. Тоді в судину можна ввести трубу, по якій подається стиснене повітря, тиск якого (Р2) визначається за допомогою манометру. Тиск Р1 відомий (наприклад, атмосферний). Збільшуємо тиск повітря.При невеликих тисках шар рідини перешкоджає виходу повітря в резервуар, але коли цей тиск досягне достатньо великого значення, спостерігається пробулькування (барботаж) повітря в резервуар. При цьому показання манометру стабілізуються (манометр показує тиск Р2).
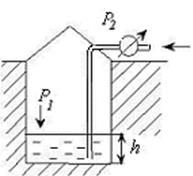
Рис. 9. Пневматичний вимір рівню рідини в резервуарі.
Позначивши (z1– z2) через h, з (1.33) отримаємо
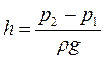 . (1.37)
. (1.37)
3) Гідравлічні машини, принцип дії яких базується на здатності рідини передавати зміну зовнішнього тиску в усі точки простору. Розглянемо роботу гідравлічного пресу, який використовують для пресування й брикетування різних матеріалів. Гідравлічний прес складається з двох цилиндрів, що сполучаються, з поршнями: поршень насосу з площею S1 і поршень пресу з площею S2 (рис. 10). Якщо до поверхні рідини прикласти силу F1 за допомогою малого поршня, то в кожній точці рідини, яка знаходиться усередині судин, що сполучаються, виникає надлишковий тиск: 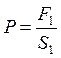 .
.
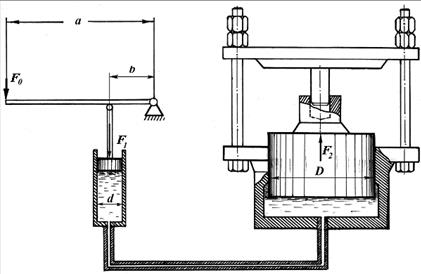
Рис. 10. Гідравлічний прес.
Цей надлишковий тиск передається в усі точки поверхні більшого поршня. Якщо знехтувати впливом ваги рідини, то сила Т2 на цю поверхню поршня буде
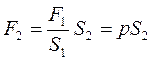 . (1.38)
. (1.38)
Для збільшення виграшу в силі в гідравлічному пресі можна використовувати важіль (див. рис. 10). При цьому, якщо знехтувати тертям
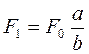 , (1.39)
, (1.39)
де F0 – сила, яка прикладена до рукоятки важіля.
Отже, сила, яка передається на більший поршень, буде
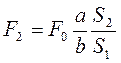 . (1.40)
. (1.40)
Дійсна сила Fд, яка стискає матеріал, внаслідок тертя в поршнях і важілі, меньша за F2, оскільки деякий вплив на величину Fд спричиняє також вага частин поршней, що рухаються. Це враховується введенням у формулу для розрахунку сили тертя коефіціента корисної дії, який дорівнює 0,85.
Тоді розрахункова формула гідравлічного пресу буде
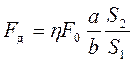 (1.41)
(1.41)
1.2.4. Гідростатичні закони для рідини, що знаходиться у відносному спокої
Відносним спокоєм рідини є такий стан, який спостерігається при відносному русі рідини разом з судиною, в якій вона перебуває і в якому усі сили, які діють на рідину, врівноважені (відносна рівновага). Вивчення основ теорії відносного спокою рідини має практичне значення. Центрифугування, відцентрове литво, гідравлічне збагачення – це лише деякі приклади, де використовується теорія відносної рівноваги. Геометричне місце точок об’єму рідини, в яких тиск однаковий, називається поверхнею рівного тиску. Поверхня рідини в судині, що межує з атмосферою, називається вільною. В усіх точках вільної поверхні тиск дорівнює Р0. Рівняння відносної рівноваги рідини можна отримати з основного диференціального рівняння гідростатики (1.34), якщо до діючих на рідину масових сил додати також сили інерції.
Розглянемо прямолінійний рівноприскорений рух судини з рідиною у горизонтальному напрямку.
Нехай судина з рідиною переміщається з прискоренням а уздовж осі х (рис. 11). Для прямокутної системи координат можна записати: Х= -а, Y=0, Z=-g. Тому диференціальне рівняння поверхні згідно з (1.32) можна подати у вигляді
Xdx + Ydy + Zdz = - adx - gdz = 0.(1.42)
Інтегруючи це рівняння, знайдемо, що
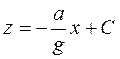 . (1.43)
. (1.43)
Сталу інтегрування можна одержати з умови, що для точки, узятої на вільній поверхні, при х = 0, z = z0.
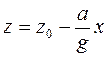 . (1.44)
. (1.44)
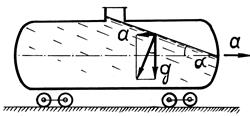
Рис.11. Резервуар з рідиною, який рухається поступово.
Отримане рівняння вільної поверхні є рівнянням площини, нахиленої до горизонту під кутом 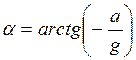 .
.
Тиск у будь-якій точці об’єму рідини згідно з (1.32) можна записати у вигляді:
dР = -r(adx+gdz).(1.45)
Після інтегрування
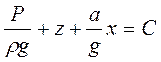 . (1.46)
. (1.46)
Сталу інтегрування С знаходимо з умови, що при х = 0 і z = z0, Р = Р0. Тоді
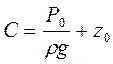 . (1.47)
. (1.47)
Рівняння (1.46) можна записати так:
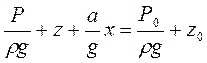 . (1.48)
. (1.48)
З цього рівняння видно, що у кожній точці вертикалі (x=const) розподіл тиску визначається за (1.46) або (1.35).
Розглянемообертання посудини з рідиною.Тут виділяємо два випадки: обертання з постійною кутовою швидкістю w навколо вертикальної осі й навколо горизонтальної осі.
· При обертанні навколо вертикальної осі (рис. 12) на кожну частинку рідини буде діяти сила ваги Мg і відцентрова сила інерції Мw2r. Рівняння вільної поверхні (dР=0) отримаємо, якщо у (1.32) підставимо значення масових сил.
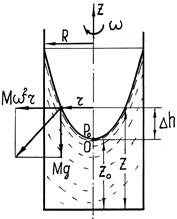
| Отримаємо:
X=w2x; Y=w2y; Z=-g;
w2xdx+ w2ydy - gz = 0.(1.49)
Після інтегрування маємо:
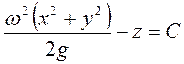 . (1.50) . (1.50)
|
| Рис. 12. Резервуар з рідиною, що обертається. |
Одержане рівняння є рівнянням сімейства параболоїдів обертання уздовж вертикальної осі. Сталу С знаходять з умови, що при х = у = 0, z = z0 і тому С = - z0. Водночас х2 + у2= r2, w×r = u, де и – лінійна швидкість обертання (м/с). Тоді (1.49) можна переписати так:
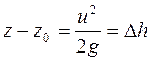 . (1.51)
. (1.51)
Величина 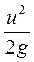 являє собою швидкісний напір і має лінійну розмірність.
являє собою швидкісний напір і має лінійну розмірність.
Закон розподілу тиску у судині знайдемо з рівняння (1.32), враховуючи (1.43):
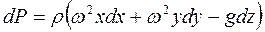 . (1.52)
. (1.52)
Після інтегрування отримаємо:
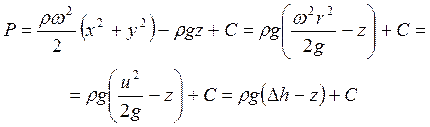 . (1.53)
. (1.53)
При z = z0величина Dh = 0 і Р = Р0, а тому С = Р0+rgz0. Отже, рівняння (1.53) перепишемо у вигляді:
Р=Р0+rg(z0- z+Dh)=Р0+rgh,(1.54)
де h = z0 – z + Dh - глибина занурення точки по вертикалі під вільну поверхню рідини.
· При обертанні посудини з постійною достатньо великою кутовою швидкістю w навколо горизонтальної осі прискорення вільного падіння g у порівнянні з відцентровим прискоренням а=w2r, що виникає, стає малим і ним можна знехтувати (g=0). У цьому разі при інтегруванні (1.32) маємо закон розподілу тиску:
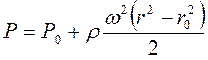 (1.55)
(1.55)
де Р0 – тиск на вільній поверхні радіусу r0;
Р - тиск у точках циліндричної поверхні довільного радіусу.
Поверхні рівню будуть являти собою циліндричні поверхні, які виражаються рівнянням:
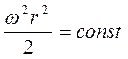 . (1.56)
. (1.56)
В техніці обертання судини з рідиною використовують у тих випадках, коли необхідно тимчасово збільшити тиск в рідині, наприклад, при відцентровому відливанні чавунних, залізобетонних та інших деталей. Відцентровий принцип полягає також в основі роботи сепараторів і центрифуг.
Дата добавления: 2015-08-26; просмотров: 986;
