Диференціальні рівняння статики Ейлера

Закони гідравліки можуть бути виражені математично через диференціальні рівняння для суцільного середовища.

В об’ємі рідини виділяємо елементарний паралелепіпед з ребрами довжиною dx, dy, dz, об’ємом dV та масою dm (рис. 7). При виведені основних закономірностей рідину вважають ідеальною, тому сили внутрішнього тертя відсутні й на паралелепіпед діють сили масова і тиску. Сила гідравлічного тиску F дорівнює добутку гідравлічного тиску Р на площу грані.

Згідно з основним законом статики сума проекцій на осі координат усіх сил, які діють на елементарний об’єм, дорівнює нулю.

Знаходимо суму проекцій сил на вісь z. Позначимо через X,Y,Z проекції масових сил, віднесених до одиниці маси, або проекції прискорення діючих сил на осі координат.

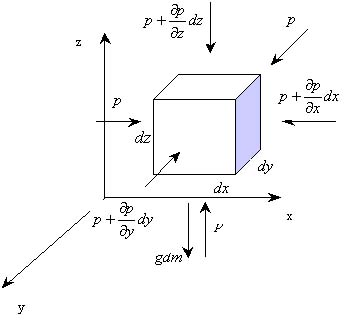
Рис. 7. До виведення рівнянь рівноваги Ейлера.

Сила масова: Zdm = ZrdV=Zrdxdydz

Сила тиску:

- на нижню грань: ;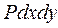

- на верхню грань: .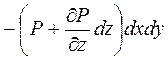

Сума проекцій усіх сил на вісь z:

,

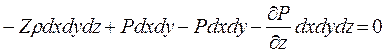або

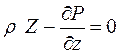. (1.29)

Аналогічно можна записати проекції сил на осі х і y:

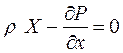, (1.30)

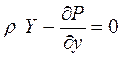. (1.31)

Рівняння (1.29-1.31) утворюють систему диференціальних рівнянь Ейлера.

Інтегруючи рівняння Ейлера, можна визначити тиск у будь-якій точці простору, зайнятого рідиною. Для цього краще замінити систему рівнянь одним диференціальним рівнянням. З цією метою помножимо рівняння (1.29) на dz, (1.30) - на dx, (1.31) - на dy і складемо їх.

В результаті одержимо:

.

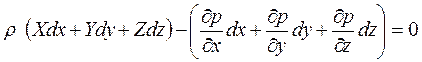Дане рівняння можна записати так:

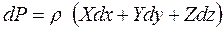. (1.32)

Це рівняння є диференціальним рівнянням гідростатики.