При равноускоренном движении
Во многих случаях ускорения, с которыми перемещаются детали машин, известны. Динамические напряжения в этих случаях вычисляются без затруднений.
Рассмотрим случай подъема груза весом G вверх с ускорением а (рис. 10.1). Определить напряжение в канате, пренебрегая его весом.
Прикладываем к грузу силу инерции, равную та = Gа/g и направленную вниз. Применим метод сечений. Делаем разрез n-п иотбрасываем верхнюю часть каната. Усилие в канате обозначаем Nд. Так как напряжения при центральном растяжении равномерно распределены по сечению, то можем принять, что Nд = sд × А, где sд – искомое динамическое напряжение.
| Рис. 10.1 |
| F |
| n |
| n |
| a |
| G |
|
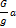
| n |
| n |
| G |
|
|
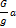
| Nд = σд ×А |
Проектируя все силы, в том числе и силы инерции, на вертикальную ось, получаем
,
откуда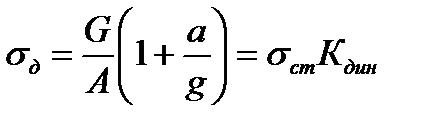 
,
где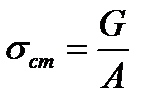 
– напряжение при статическом действии груза;
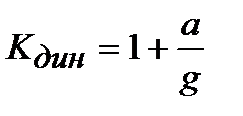– динамический коэффициент.
Таким образом, динамические напряжения могут быть выражены через статические напряжения и динамический коэффициент. Это особенно удобно, так как величину динамического коэффициента часто приходится определять опытным путем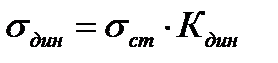 
.
Дата добавления: 2015-08-21; просмотров: 807;