Лекция 7 .

Непрерывно-стохастические модели (Q-схемы)

Особенности непрерывно-стохастического подхода рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания (англ. queueing system), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например заявки на обработку информации ЭВМ от удаленных терминалов и т.д. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т.е. стохастический характер процесса их функционирования. В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно изобразить в виде некоторого i-го прибора обслуживанияП_i, состоящего из накопителя заявок H_i, в котором может одновременно находиться 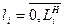заявок, где L_i^H—емкость i-го накопителя, и канала обслуживания заявок (или просто канала) К_i. На каждый элемент прибора обслуживания П_i поступают потоки событий: в накопитель H_i — поток заявок w_i на канал К_i – поток обслуживании u_i.

В практике моделирования систем, имеющих более сложные структурные связи и алгоритмы поведения, для формализации используются не отдельные приборы обслуживания, а Q-схемы, образуемые композицией многих элементарных приборов обслуживания П_i (сети массового обслуживания). Если каналы K_i различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы П_i и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Таким образом, для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой. Различают разомкнутые и замкнутые Q-схемы. В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т. е. обратная связь отсутствует, а в замкнутых Q-схемах имеются обратные связи, по которым заявки двигаются в направлении, обратном движению вход-выход.

Возможности оценки характеристик с использованием аналитических моделей теории массового обслуживания являются весьма ограниченными по сравнению с требованиями практики исследования и проектирования систем, формализуемых в виде Q-схем. Несравненно большими возможностями обладают имитационные модели, позволяющие исследовать Q-схему, задаваемую без ограничений.

Сетевые модели (N-схемы)

В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распространенным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (от англ. Petri Nets).

Формально сеть Петри (N-схема) задается четверкой вида:

,

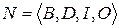где В – конечное множество символов, называемых позициями; D – конечное множество символов, называемых переходами; I – входная функция (прямая функция инцидентности); O – выходная функция (обратная функция инцидентности). Таким образом, входная функция I отображает переход d_j в множество выходных позиций b_iÎI(d_j), а выходная функция О отображает переход d_j в множество выходных позиций b_iÎD(d_j).

Графически N-схема изображается в виде двудольного ориентированного мультиграфа, представляющего собой совокупность позиций и переходов. Граф N-схемы имеет два типа узлов: позиции и переходы, изображаемые 0 и 1 соответственно. Ориентировочные дуги соединяют позиции и переходы, причем каждая дуга направлена от элемента одного множества (позиции или перехода) к элементу другого множества (переходу или позиции). Граф N-схемы является мультиграфом, так как он допускает существование кратных дуг от одной вершины к другой.

Приведенное представление N-схемы может использоваться только для отражения статики моделируемой системы (взаимосвязи событий и условий), но не позволяет отразить в модели динамику функционирования моделируемой системы. Для представления динамических свойств объекта вводится функция маркировки (разметки) М: B®{0, 1, 2, ...}. Маркировка М есть присвоение неких абстрактных объектов, называемых метками (фишками), позициям N-схемы, причем количество меток, соответствующее каждой позиции, может меняться. При графическом задании N-схемы разметка отображается помещением внутри вершин-позиций соответствующего числа точек (когда количество точек велико, ставят цифры). Маркированная (размеченная) N-схема может быть описана в виде пятерки 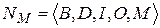и является совокупностью сети Петри и маркировки М.

Функционирование N-схемы отражается путем перехода от разметки к разметке. Начальная разметка обозначается как М₀: В®{0, 1, 2, ...}. Смена разметок происходит в результате срабатывания одного из переходов d_jÎD сети. Необходимым условием срабатывания перехода d_j является b_iÎI(d_j) {M(b_i)³ 1}, где М(b_i) – разметка позиции b_i. Переход d_j, для которого выполняется указанное условие, определяется как находящийся в состоянии готовности к срабатыванию или как возбужденный переход.

Комбинированные модели (A-схемы)

Наиболее известным общим подходом к формальному описанию процессов функционирования систем является подход, предложенный Я.П. Бусленко. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем, т. е. по сравнению с рассмотренными является обобщенным (универсальным) и базируется на понятии агрегативной системы (от англ. aggregate system), представляющей собой формальную схему общего вида, которую будем называть А-схемой.

Анализ существующих средств моделирования систем и задач, решаемых с помощью метода моделирования на ЭВМ, неизбежно приводит к выводу, что комплексное решение проблем, возникающих в процессе создания и машинной реализации модели, возможно лишь в случае, если моделирующие системы имеют в своей основе единую формальную математическую схему, т.е. А-схему. Такая схема должна одновременно выполнять несколько функций: являться адекватным математическим описанием объекта моделирования, т. е. системы S, служить основой для построения алгоритмов и программ при машинной реализации модели М, позволять в упрощенном варианте (для частных случаев) проводить аналитические исследования.

Приведенные требования в определенной степени противоречивы. Тем не менее, в рамках обобщенного подхода на основе А-схем удается найти между ними некоторый компромисс.

По традиции, установившейся в математике вообще и в прикладной математике в частности, при агрегативном подходе сначала дается формальное определение объекта моделирования – агрегативной системы, которая является математической схемой, отображающей системный характер изучаемых объектов. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. Если некоторые из полученных подсистем оказываются в свою очередь еще достаточно сложными, то процесс их разбиения продолжается до тех пор, пока не образуются подсистемы, которые в условиях рассматриваемой задачи моделирования могут считаться удобными для математического описания. В результате такой декомпозиции сложная система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, объединенных в подсистемы различных уровней.

В качестве элемента А-схемы выступает агрегат, а связь между агрегатами (внутри системы S и с внешней средой Е) осуществляется с помощью оператора сопряжения R. Очевидно, что агрегат сам может рассматриваться как А-схема, т. е. может разбиваться на элементы (агрегаты) следующего уровня. Любой агрегат характеризуется следующими множествами: моментов времени Т, входных Х и выходных Y сигналов, состояний Z в каждый момент времени t. Состояние агрегата в момент времени tÎT обозначается как z(t)ÎZ, а входные и выходные сигналы — как х(t)ÎХ и у(t)ÎY соответственно.

Существует класс больших систем, которые ввиду их сложности не могут быть формализованы в виде математических схем одиночных агрегатов, поэтому их формализуют некоторой конструкцией из отдельных агрегатов A_n, 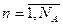, которую назовем агрегативной системой или А-схемой. Для описания некоторой реальной системы S в виде А-схемы необходимо иметь описание как отдельных агрегатов A_n, так и связей между ними.

Функционирование А-схемы связано с переработкой информации. Вся информация, циркулирующая в А-схеме, делится на внешнюю и внутреннюю. Внешняя информация поступает от внешних объектов, не являющихся элементами рассматриваемой схемы, а внутренняя информация вырабатывается агрегатами самой А-схемы. Обмен информацией между А-схемой и внешней средой Е происходит через агрегаты, которые называются полюсами А-схемы. При этом различают входные полюсы А-схемы, представляющие собой агрегаты, на которые поступают х-сообщения, и выходные полюсы А-схемы, выходная информация которых является у-сообщениями. Агрегаты, не являющиеся полюсами, называются внутренними.