Лекция 5 .

Непрерывно-детерминированные модели (D-схемы)

Рассмотрим особенности непрерывно-детерминированного подхода на примере использования в качестве математических моделей дифференциальных уравнений. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной или нескольких переменных, причем в уравнение входят не только функции, но и их производные различных порядков. Если неизвестные — функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае при рассмотрении функции только одной независимой переменной уравнения называются обыкновенными дифференциальными уравнениями (ОДУ).

Обычно в таких математических моделях в качестве независимой переменной, от которой зависят неизвестные искомые функции, служит время t. Тогда математическое соотношение для детерминированных систем (2.6) в общем виде будет

,

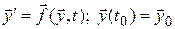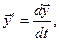
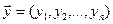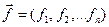где и - n-мерные векторы; - вектор-функция, которая определена на некотором (п+1)-мерном множестве и является непрерывной. Так как математические схемы такого вида отражают динамику изучаемой системы, т.е. ее поведение во времени, то они называются D-схемами (от англ. dynamic).

В простейшем случае ОДУ имеет вид:

,

где h₀, h₁, h₂ – параметры системы; z(t) – состояние системы в момент времени t.

Если изучаемая система взаимодействует с внешней средойЕ, то появляется входное воздействие х(t)и непрерывно-детерминированная модель такой системы будет иметь вид:

.

С точки зрения общей схемы математической модели х(t)является входным (управляющим) воздействием, а состояние системы S в данном случае можно рассматривать как выходную характеристику, т.е. полагать, что выходная переменная совпадает с состоянием системы в данный момент времени y=z.

При решении задач системотехники важное значение имеют проблемы управления большими системами. Следует обратить внимание на системы автоматического управления – частный случай динамических систем, описываемых D-схемами и выделенных в отдельный класс моделей в силу их практической специфики. Описывая процессы автоматического управления, придерживаются обычно представления реального объекта в виде двух систем: управляющей и управляемой (объекта управления).

. Лекция 6 .

Дискретно-детерминированные модели (F-схемы)

Особенности дискретно-детерминированного подхода на этапе формализации процесса функционирования систем рассмотрим на примере использования в качестве математического аппарата теории автоматов. Теория автоматов – это раздел теоретической кибернетики, в котором изучаются математические модели – автоматы. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции и целесообразной степени общности. Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний а, следовательно, и множество выходных сигналов являются конечными множествами. Абстрактно конечный автомат (от англ. finite automat) можно представить как математическую схему, характеризующуюся шестью элементами: конечным множеством Х входных сигналов (входным алфавитом); конечным множеством Y выходных сигналов (выходным алфавитом); конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием z₀ÎZ; функцией переходов j(z, x); функцией выходов y(z, x).

Автомат, задаваемый F-схемой: 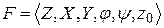– функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Если обозначить состояние, а также входной и выходной сигналы, соответствующие t-му такту при t = 0, 1, 2, ..., через z(t), x(t), y(t).При этом z(0)=z₀, z(t)ÎZ, x(t)ÎX, y(t)ÎY. Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент дискретного времени F-автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=z₀. В момент t, будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал x(t)ÎX и выдать на выходном канале сигнал у(t)=y [z(t), х(t)], переходя в состояние z(t+1)=j [z(t), x(t)], x(t)ÎX, y(t)ÎY. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита Х на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z₀, подавать в некоторой последовательности буквы входного алфавита х(0), х(1), х(2),..., т.e. входное слово, то на выходе автомата будут появляться буквы выходного алфавита у(0), y(1), у(2), ..., образуя выходное слово. Таким образом, работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t+1) и выдачей некоторого выходного сигнала.

По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F-автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. Асинхронный F-автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом.

Дискретно-стохастические модели (P-схемы)

Рассмотрим особенности построения математических схем при дискретно-стохастическом подходе к формализации процесса функционирования исследуемой системы. Так как сущность дискретизации времени при этом подходе остается аналогичной рассмотренным в конечным автоматам, то влияние фактора стохастичности проследим также на разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.

В общем виде вероятностный автомат(англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Применение схем вероятностных автоматов имеет важное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.

Введем математическое понятие Р-автомата, используя понятия, введенные для F-автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (x_i, z_s), где х_i, и z_s – элементы входного подмножества Х и подмножества состояний Z соответственно. Если существуют две такие функции j и y, то с их помощью осуществляются отображения G®Z и G®Y, то говорят, что определяет автомат детерминированного типа. Введем в рассмотрение более общую математическую схему. Пусть Ф – множество всевозможных пар вида (z_k, y_i) где у_j – элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

Элементы из Ф … (z₁, y₁) … (z₁, y₂) … … (z_K, y_J-1) (z_K, y_J)

(x_i z_k) … b₁₁ b₁₂… b_K(J-1) b_KJ

При этом ,

где b_kj – вероятности перехода автомата в состояние z_k и появления на выходе сигнала у_j, если он был в состоянии z_s и на его вход в этот момент времени поступил сигнал х_i. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В, тогда четверка элементов называется вероятностным автоматом (Р-автоматом).