Лекция №2.
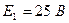 ;
; 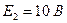 ;
; 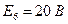 ;
;
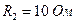 ;
;  ;
; 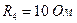 ;
; 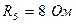 ;
; 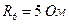 ;
;
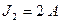 ;
;
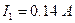 ;
; 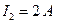 ;
; 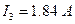 ;
; 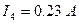 ;
; 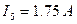 ;
; 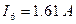 ;
;
Потенциальная диаграмма – график распределения потенциала вдоль участка цепи или замкнутого контура. По оси абсцисс откладывают величины сопротивлений, суммируя их. По оси ординат откладывают потенциалы точек цепи. Потенциал какой-нибудь одной точки можно принять за ноль и относительно него определять потенциалы других точек цепи.
Построим потенциальную диаграмму для контура 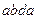 , при этом потенциал точки
, при этом потенциал точки 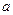 примем за ноль.
примем за ноль.
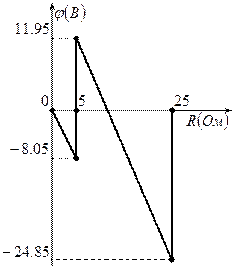
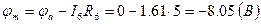 ;
;
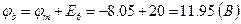 ;
;
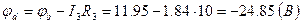 ;
;
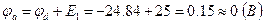 ;
;
Энергетический баланс.
При протекании токов по сопротивлениям цепи в них выделяется тепло. На основании закона сохранения энергии, количество тепла, выделяющегося в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой в цепь за тоже время источниками питания, то есть мощность, выделяющаяся в сопротивлениях нагрузки, должна быть равна мощности, доставляемой источниками. Количество тепла, выделяющегося в единицу времени в резисторе с сопротивлением 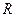 , по которому течёт ток
, по которому течёт ток 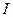 , можно найти по формуле:
, можно найти по формуле: 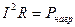 . Если резисторов несколько, то
. Если резисторов несколько, то 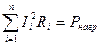 .
.
Если ток течёт через ЭДС сонаправленную с током, то 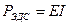 , если ток течёт через ЭДС, направленной против тока, то
, если ток течёт через ЭДС, направленной против тока, то 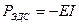 , и ЭДС, в этом случае, будет являться потребителем тока.
, и ЭДС, в этом случае, будет являться потребителем тока.
Если ток течёт через источник тока, то напряжение на источнике тока будет равно произведению напряжения на концах источника тока на ток источника тока, то есть 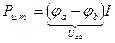 , при этом напряжение на концах источника тока определяется по внешней цепи.
, при этом напряжение на концах источника тока определяется по внешней цепи.
Вернёмся к нашей цепи и посчитаем для неё баланс мощности:
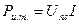 ;
; 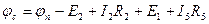 ;
; 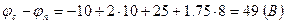 ;
;
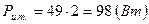 .
.
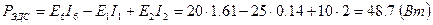 .
.
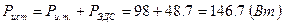 .
.
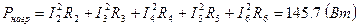 .
.
Принцип (метод) наложения.
Ток в любой ветви электрической цепи равен алгебраической сумме токов, вызываемых каждым источником цепи в отдельности, поэтому определяют токи в ветвях, возникающие от действия каждого источника, удаляя из цепи все остальные источники, но учитывая их внутренние сопротивления. Так как у источников ЭДС внутреннее сопротивление равно нулю, то их закорачивают. Так как у источников тока внутреннее сопротивление бесконечно большое, то ветви, содержащие источники тока, разрывают. Затем определяют токи в ветвях, путём алгебраического сложения частичных токов с учётом их направления.
Пример:
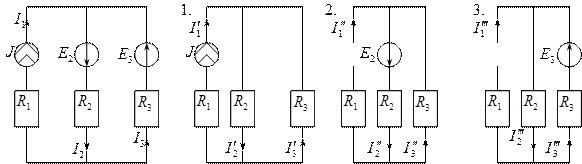
Дано:
 .
.
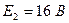 ;
; 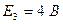 .
.
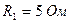 ;
; 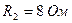 ;
; 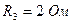 .
.
Задание: определить токи в ветвях методом наложения.
Первый этап: оставляем источник тока, а источники ЭДС удаляем с учётом их внутреннего сопротивления.
Воспользуемся формулой разброса токов:
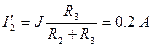 ;
;
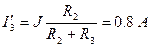 .
.
Проверка: 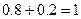 .
.
Второй этап: оставляем источник ЭДС 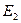 , а источник тока и источник ЭДС
, а источник тока и источник ЭДС 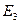 удаляем, с учётом их внутренних сопротивлений.
удаляем, с учётом их внутренних сопротивлений.
Ток в цепи можно найти по формуле:
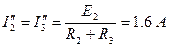 .
.
Третий этап: оставляем источник ЭДС 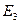 , а источник тока и источник ЭДС
, а источник тока и источник ЭДС 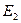 удаляем, с учётом их внутренних сопротивлений.
удаляем, с учётом их внутренних сопротивлений.
Ток в цепи можно найти по формуле:
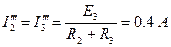 .
.
Четвёртый этап: определяем токи в ветвях с учётом направления частичных токов.
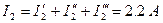 ;
;
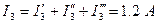 .
.
Проверка по первому закону Кирхгофа: 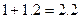 .
.
Так же можно провести проверку по балансу мощностей.
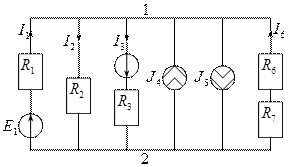 Метод двух узлов.
Метод двух узлов.
Часто встречаются схемы, содержащие два узла. Наиболее рациональным методом является метод двух узлов. За неизвестную величину принимают напряжение между двумя узлами и определяют его по формуле:  . ЭДС источников и токи источников тока, направленные к точке 1 войдут в эту формулу с положительным знаком, а ЭДС источников и токи источников тока, направленные к точке 2 войдут в эту формулу с отрицательным знаком.
. ЭДС источников и токи источников тока, направленные к точке 1 войдут в эту формулу с положительным знаком, а ЭДС источников и токи источников тока, направленные к точке 2 войдут в эту формулу с отрицательным знаком.
Для нашей схемы: 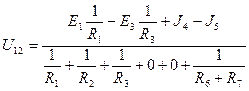 .
.
Определяем токи в ветвях по закону Ома:
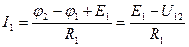 ;
;
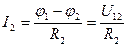 ;
;
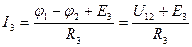 ;
;
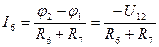 .
.
После расчёта токов необходимо провести проверку по первому закону Кирхгофа.
Метод контурных токов.
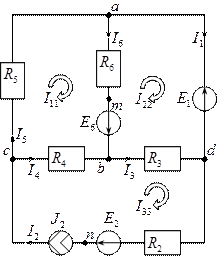
Обратимся к первой схеме.
Число уравнений, которых необходимо составить, равно числу уравнений, которых необходимо составить по второму закону Кирхгофа, или числу независимых контуров. Предполагают, что в каждом контуре течёт свой контурный ток.
В случае, когда в цепи три контурных тока, записывают систему уравнений следующим образом: 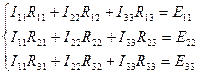 . В данном случае один из контурных токов известен, а именно ток
. В данном случае один из контурных токов известен, а именно ток  , который равен току источника тока
, который равен току источника тока 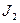 , поэтому система будет состоять из двух уравнений.
, поэтому система будет состоять из двух уравнений.
Сформируем коэффициенты:
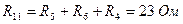 - сумма сопротивлений первого контура.
- сумма сопротивлений первого контура.
 - сумма сопротивлений второго контура.
- сумма сопротивлений второго контура.
 - сопротивление общей ветви между первым и вторым контурами, взятое в данном случае с отрицательным знаком, так как контурные токи текут через это сопротивление в противоположенные стороны, то есть навстречу друг другу.
- сопротивление общей ветви между первым и вторым контурами, взятое в данном случае с отрицательным знаком, так как контурные токи текут через это сопротивление в противоположенные стороны, то есть навстречу друг другу.
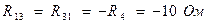 - сопротивление общей ветви между первым и третьим контурами, взятое в данном случае с отрицательным знаком, так как контурные токи текут через это сопротивление в противоположенные стороны, то есть навстречу друг другу.
- сопротивление общей ветви между первым и третьим контурами, взятое в данном случае с отрицательным знаком, так как контурные токи текут через это сопротивление в противоположенные стороны, то есть навстречу друг другу.
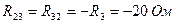 - сопротивление общей ветви между вторым и третьим контурами, взятое в данном случае с отрицательным знаком, так как контурные токи текут через это сопротивление в противоположенные стороны, то есть навстречу друг другу.
- сопротивление общей ветви между вторым и третьим контурами, взятое в данном случае с отрицательным знаком, так как контурные токи текут через это сопротивление в противоположенные стороны, то есть навстречу друг другу.
В случае, когда токи направлены в одну сторону сопротивление берётся положительным.
 - контурная ЭДС первого контура, равная сумме ЭДС входящих в первый контур, взятая в данном случае с положительным знаком, так как направление ЭДС совпадает с направлением обхода контура.
- контурная ЭДС первого контура, равная сумме ЭДС входящих в первый контур, взятая в данном случае с положительным знаком, так как направление ЭДС совпадает с направлением обхода контура.
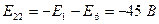 - контурная ЭДС второго контура, равная сумме ЭДС входящих во второй контур, взятых в данном случае с отрицательными знаками, так как направления этих ЭДС не совпадают с направлением обхода контура.
- контурная ЭДС второго контура, равная сумме ЭДС входящих во второй контур, взятых в данном случае с отрицательными знаками, так как направления этих ЭДС не совпадают с направлением обхода контура.
Получаем систему уравнений: 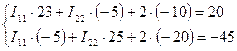 .
.
Дата добавления: 2015-08-21; просмотров: 662;
