Лекция №6.

Рассмотрим схему:

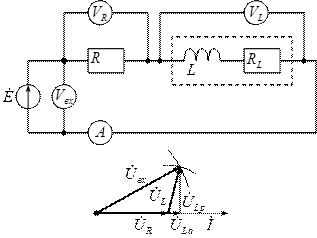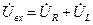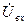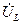Диаграмму для напряжений строится по второму закону Кирхгофа: . Так как неизвестны сдвиги по фазам напряжений и , то они строятся с помощью метода засечек. Строятся окружности радиусом 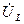и 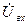из конца и начала вектора 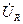соответственно. Эти окружности пересекаются в двух точках. Исходя из физического смысла, выбираем верхнюю точку. Соединив точку пересечения с началом и концом вектора 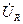, можно получить расположение векторов 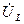и 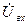. Проекция вектора 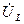на ось действительных чисел даст нам вектор активного сопротивления катушки 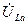, а на ось комплексных чисел – вектор реактивного сопротивления катушки.

Топографическая диаграмма.

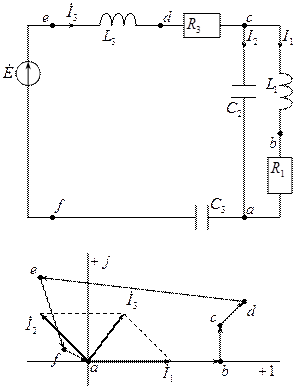Потенциал какой-нибудь одной точки, например точки 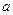, принимается за ноль, то есть 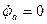. Затем определяются потенциалы точек цепи и положение их на комплексной плоскости.

;

;

;

;

;

;

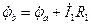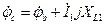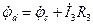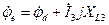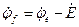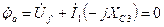Резонансный режим

работы двухполюсника.

Явление резонанса возможно в цепи, которая содержит реактивные элементы разного знака, то есть в цепи, которая содержит индуктивность и ёмкость.

Резонанс – режим, при котором то к и напряжение на входе двухполюсника совпадают по фазе, то есть разность фаз 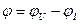равна нулю. Это основное условие любого резонанса. По отношению к внешней цепи двухполюсник ведёт себя, как активное сопротивление.

Различают два вида резонансов: резонанс токов и резонанс напряжений.

Резонанс токов.

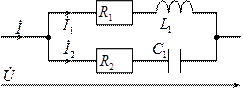При параллельном соединении катушки индуктивности и конденсатора возникает резонанс токов при определённых условиях.

Определим токи:

;

;

.

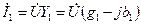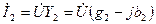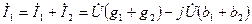Из полученного уравнения и из основного условия резонанса 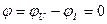можно получить условие резонансов токов: 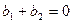. Так как 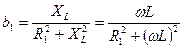, а 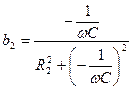, то условие резонансов токов приобретает следующий вид: .

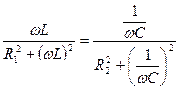Построим векторную диаграмму.

Если активные внутренние сопротивления катушки индуктивности и конденсатора не равны нулю, то , .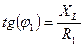

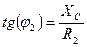Если активное внутреннее сопротивление конденсатора очень мало, то условие резонанса токов примет следующий вид: .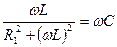

Если активные внутренние сопротивления катушки и индуктивности и конденсатора равны нулю, то условие резонанса примет следующий вид: 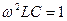, откуда 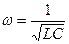. При этом .

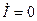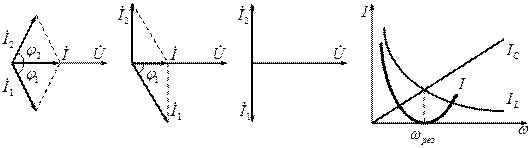
Ток, текущий через катушку индуктивности можно найти по формуле: 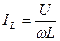. Если 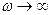, то ток через катушку индуктивности будет равен нулю, то есть .

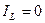Реактивные проводимости: ; ; .

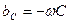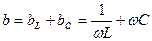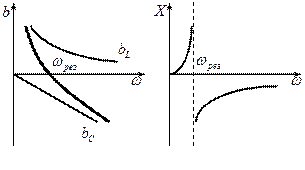
Задачи:

Требуется построить зависимость токов через катушку и конденсатор, в зависимости от ёмкости конденсатора .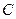

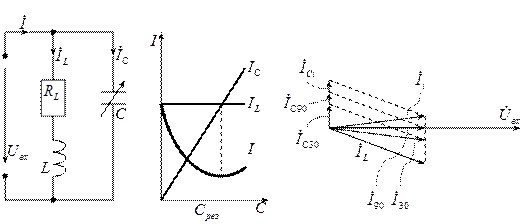
Ток, текущий через катушку индуктивности, можно найти по следующей формуле: 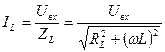. Из этой формулы видно, что ток, текущий через катушку индуктивности, не зависит от ёмкости конденсатора.

Если ёмкость конденсатора 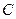равна нулю, тогда 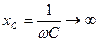, следовательно, ток, текущий через конденсатор, 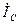равен нулю, а ток 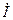, который равен сумме токов, текущих через катушку индуктивности и конденсатор, будет равен току, текущему через катушку индуктивности .

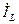При увеличении ёмкости конденсатора 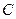будет увеличиваться ток, текущий через него .

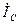Компенсация сдвига фаз.

Входное сопротивление большинства потребителей электроэнергии имеют индуктивный характер. Для того, чтобы уменьшить потребляемый ток и тем самым снизить потери энергии, параллельно приёмнику подключают батарею конденсатора, то есть добиваются режима резонанса тока. Этот процесс называют компенсацией сдвига фаз. Обычно величину 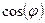доводят до значений 0.9-0.95. Компенсация сдвига фаз особенно важна для энергоёмких потребителей.

Резонанс напряжений.

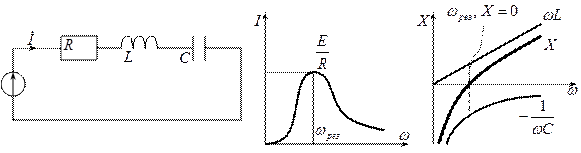
В цепи, в которой включены последовательно конденсатор, катушка индуктивности и конденсатор, возможно возникновение резонанса напряжений при определённых условиях. Ток, текущий в цепи можно найти по формул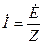е: , где 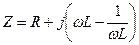. Если нужно чтобы сдвиг по фазе между напряжениями равнялся нулю, то надо чтобы 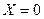. Следовательно, 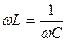- условие резонанса напряжений, при этом резонансную частоту можно найти по формуле: 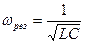. При резонансе 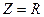, а ток .

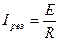Построим векторную диаграмму по второму закону Кирхгофа:

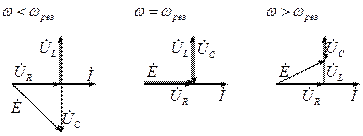Отношение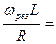 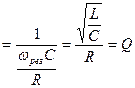называют добротностью.

Добротность – величина, показывающая во сколько раз напряжение на реактивном элементе при резонансе больше чем напряжение на входе, то есть .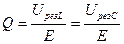

Построим графики напряжений в зависимости от частоты.

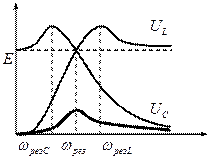Напряжение на катушке индуктивности можно найти по формуле: 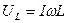. При 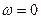напряжение на катушке индуктивности будет равняться нулю, при 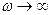напряжение на катушке индуктивности будет равняться ЭДС источника, то есть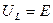

Напряжение на конденсаторе можно найти по формуле: 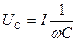. Если 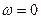, то напряжение на конденсаторе равно ЭДС источника, то есть .

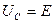Видно, что графики имеют ярко выраженныемаксимумы.