Умови і ситуації вироблення рішень
Метод вибору рішень у значній мірі залежить від умов і виду розв'язуваного завдання.
При вирішенні простих завдань (в умовах визначеності), що мають мало перемінних, що роблять вплив на результат, вибрати варіант вирішення можна за допомогою розрахунків економічної ефективності різних варіантів, як це робиться, наприклад, при виборі варіантів технологічного процесу.
При вирішенні складних завдань, коли приходиться враховувати вплив багатьох перемінних, успішно застосовується математичне моделювання, за допомогою чого оптимальний варіант можна вибрати з залежностей, що були закладені в алгоритмі, і з установленого критерію оцінки ефективності.
В умовах визначеності на виробництві зважуються багато завдань короткострокової дії, наприклад, визначення раціональних розмірів партії запуску і випуску виробів і т.д. [3].
Звичайно окремі неоптимальні рішення таких завдань не приносять великого збитку виробництву. Однак ЛПР варто враховувати, що такі завдання виникають систематично, а тому при багаторазовому повторенні навіть відносно невеликі втрати в окремих випадках можуть привести, у кінцевому рахунку, до значного зниження ефективності. Отже, при вирішенні таких завдань потрібно шукати найбільш оптимальні варіанти, розрахунок яких виробляється, як правило, за допомогою різних методів і прийомів математичного моделювання.
Відносна простота завдань, розв'язуваних в умовах визначеності, іноді приводить до ігнорування ЛПР об'єктивних різних умов, що найчастіше приводить до помилки у вирішенні питань, а виходить, і до додаткових витрат виробництва.
При виборі рішень передбачається, що особа, що приймає рішення з достатньою точністю знає ймовірності виникнення різних подій, що роблять вплив на рішення. Це може бути досягнуте на основі знань і досвіду, накопичених ЛПР, і спеціальних досліджень виробничої обстановки. Такі дослідження дають гарні результати для часто повторюваних ситуацій, тому що дозволяють виявити визначені закономірності і причини появи подій. Знаючи причини, можна більш об'єктивно і точно визначити, які міри необхідно прийняти для того, щоб запобігти виникненню небажаних ситуацій.
Оцінки ймовірності для завдань щодо короткострокової дії звичайно можуть бути визначені з більшою вірогідністю, ніж для завдань перспективних.
В умовах ризику, можуть зважуватися такі завдання, як: визначення оптимальної чисельності і раціонального розміщення обслуговуючого персоналу; вибір мір для ритмічного ходу виробництва і зниження собівартості; запобігання порушень, що перешкоджають безперебійному випуску продукції по всій номенклатурі і т.д.
Елемент ризику в процесі вироблення рішень виявляється тоді, коли не можна вірогідно пророчити очікувані результати тих чи інших дій. У тих випадках, коли підстави для прогнозування результатів недостатні, рекомендується зробити спробу визначити найкращий і найгірший результати дій.
У деяких випадках для вибору рішень буває досить зіставлення результатів. Якщо ж це не представляється можливим, то варто спробувати хоча б приблизно визначити витрати, що бу- дуть потрібні для реалізації рішень. Якщо витрати порівняно невеликі, можна вважати рішення задовільним, тому що в цьому випадку ризик втрат невеликий. При великих витратах необхідні додаткові дослідження для того, щоб одержати повну інформацію для зменшення ризику.
Нагромадження інформації в процесі вирішення завдань дозволяє зменшити невизначеність результатів, а реалізація рішення стає сама джерелом інформації.
Таким чином, невизначеність зменшується не тільки завдяки умінню керівника пророчити достовірні результати вирішення завдань, але також і завдяки його здатності приймати нові рішення, коли очікувані результати не отримані.
Для того, щоб зробити прогноз можливості виникнення об'єктивних різних умов, ЛПР необхідно виявити наступне:
1. Які об'єктивні умови можуть вплинути на результати
того чи іншого рішення?
2. Чи можна передбачати виникнення всіх можливих
об'єктивних умов?
3. Чи можна встановити частоту виникнення тих чи
інших об'єктивних умов?
4. Чи постійна ця частота?
Передбачивши виникнення різних об'єктивних умов і визначивши варіанти рішень, можна встановити очікувані результати по кожному з їхніх сполучень у показниках, що відбивають ступінь досягнення цілей.
Очікувані результати вирішення завдань в умовах невизначеності можна визначити трьома способами:
1. За допомогою оцінок очікуваних результатів рішень і
припущень.
2. На основі спостережень і результатів експерименту.
3. На основі співвідношень, по яких попередньо бу
дується гіпотеза, наприклад, по аналізі.
Можливе використання комбінацій цих способів.
Часто застосовується перший спосіб оцінки очікуваних результатів. Розглядаючи варіанти рішень, керівник прикидає, які результати можна чекати від того чи іншого варіанта в різних умовах.
У зв'язку з тим, що в основу цього методу покладено суб'єктивний початок, не виключені помилки, і тому найчастіше При його використанні залучають експертів.
Застосовуючи другий метод для одержання показникіп результату рішення на основі спостережень і підсумків експери менту, можна зробити більш правильні висновки. Але цей спосіп вимагає значних витрат засобів і часу. І якщо ці обмеження їй лімітують ЛПР, то його можна використовувати.
vi Третій метод оцінки результатів рішень передбачає вико ристання аналітичних засобів, таких, як математичні рівняння чи сукупність логічних положень. Цей підхід прийнятний для вирішення багатьох завдань керування виробництвом.
Застосовуючи кожний з трьох методів визначення очікуваних результатів рішень при об'єктивних різних умовах, для зручності аналізу можна звести всі отримані дані в таблицю, названу матрицею рішень чи платіжною матрицею.
Позначимо об'єктивні умови через Vj, де j — кількість об'єктивних різних умов (1 ≤ j ≤ m).
Варіанти рішень (стратегій) позначимо через Сi де i - кількість варіантів.
Результат, очікуваний при кожнім сполученні варіанті в рішення й об'єктивних умов, позначимо через Оij.
Тоді матриця рішень при j = 3 і i = 4 буде мати вигляд:
| V1 | V2 | V3 | |
| C1 | O11 | O12 | O13 |
| C2 | O21 | O22 | O23 |
| C3 | O31 | O32 | O33 |
| C4 | O41 | O42 | O43 |
Така матриця результатів рішень універсальна. Вона може бути використана при вирішенні найрізноманітніших завдань. Об'єктивні умови в матриці відбивають нерегульовані фактори, що можуть вплинути на результати рішень, а показники результату характеризують те, що буде досягнуто при виборі даного варіанта рішення і виникненні визначених об'єктивних умов.
Слід зазначити, що складання матриці не може бути зведене до яких-небудь механічних дій. Керівнику необхідно добре знати виробництво, мати визначений досвід роботи і творче мислення. Тільки в цьому випадку він зможе з достатньою вірогідністю уявити, які ситуації (об'єктивні умови) можуть виникнути і який вплив вони зроблять на виробництво.
Особливу увагу ЛПР повинні звертати на стабільність виробничої системи, під якою розуміється ритмічна робота Підприємства протягом тривалого періоду. При стабільній системі ймовірність випадків менше, у зв'язку з чим і менше ймовірність помилитися в процесі ухвалення рішення.
Матриця рішень дозволяє здійснити вибір рішень в умовах ризику, тому що в ній враховується ймовірність появи тих чи інших об'єктивних умов. Такий вибір виробляється на основі встановлених ймовірностей виникнення різних умов і результатів, очікуваних при цих обставинах, шляхом визначення математичного чекання (середнього значення результату кожного з варіантів).
Позначимо через Рj ймовірність виникнення тих чи інших об'єктивних умов Vj Сума ймовірностей (∑Рj) виникнення можливих умов Vj дорівнює одиниці, що можна записати в такий спосіб (при кількості можливих станів m)

Оскільки сума ймовірностей дорівнює одиниці, математичне чекання можна виразити формулою
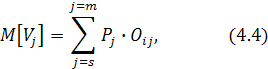
тобто, середнє значення результатів і-го варіанта рішення дорівнює сумі добутків кожної з величин результатів по всіх розглянутих об'єктивних умовах на відповідні ймовірності їхнього виникнення.
Підставивши у формулу (4.4) значення ймовірностей Р1, Р2, Р3 і значення очікуваних результатів при кожнім сполученні варіантів рішення й об'єктивних умов Оij і зробивши необхідні розрахунки, можна здійснити досить обґрунтований вибір варіанта рішення шляхом зіставлення середніх значень результатів.
Вирішення завдань в умовах невизначеності являє собою найбільші труднощі, тому що для них неможливо зробити достовірний прогноз чи оцінити ймовірність дії об'єктивних різних умов. Вирішення таких завдань не можна звести до складання і вирішення математичної моделі, як це робиться для завдань, розв'язуваних в умовах визначеності і ризику.
Вибір рішень в умовах невизначеності, так само, як і в умовах ризику (коли немає достатньої довіри до оцінок), може здійснюватися тільки керівником, що вибирає найбільш кращі варіанти з його погляду.
Велике значення при цьому мають іноді індивідуальні особливості керівника. Найбільш обережні звичайно прагнуть уникати якого-небудь ризику і вибирають той варіант рішення, Що забезпечує мінімальні втрати при обстановці, що несприятливо складається, — правило мінімізації максимального збитку (результат мінімаксу).
Керівник — оптиміст часто прагне вибрати такий варіант рішення, що дасть найкращий із усіх кращих результатів, незважаючи на те, що при несприятливих обставинах він може принести великі втрати. Цей результат називають максимаксом.
Наявність альтернативних ситуацій породжує невизначеність вибору оптимального рішення. Для усунення цієї невизначеності можна використовувати два шляхи.
Перший з них полягає в тім, що для кожної окремо узятої ситуації визначається своє оптимальне рішення. Застосування конкретного рішення зв'язано з появою конкретної ситуації. Очевидно, що цей шлях можливий тільки в тому випадку, коли можна чекати появи цієї конкретної ситуації. Характерним прикладом такого підходу є інструкція дій на випадок пожежі.
Другий шлях усунення невизначеності застосовується в тому випадку, коли рішення повинно бути прийняте до одержання інформації про те, яка в дійсності ситуація має місце. Сутність цього шляху полягає в обліку впливу всіх ситуацій на вибір оптимального рішення.
Можливі різні способи обліку цього впливу, що відрізняються між собою характером прийнятої стратегії дії ЛПР і вибором конкретного критерію оптимальності. Два з них ми вже розглянули.
Третій вид стратегії зветься раціональною, девізом якої є висловлення "Розраховуй на найбільш ймовірні умови". При цьому прораховуються ймовірності появи тих чи інших ситуацій, здатних вплинути на намічувані результати, і розробляються міри, що їх усувають. Часто такий підхід називають критерієм максимального середнього виграшу.
У ряді випадків ЛПР утрудняється обґрунтовано вибрати критерій одержання оптимального рішення. У цих випадках доцільно провести аналіз різних критеріїв. Для цього необхідно за річними критеріями вибрати оптимальні рішення, визначити, чи збігаються розрізняються між собою ці рішення, і оцінити вплив Критеріїв на вибір оптимального рішення. Такий аналіз дозволяє ЛПР більш осмислено і логічно вибирати критерій і відповідне йому оптимальне рішення.
Дата добавления: 2015-08-21; просмотров: 831;
