Сила притяжения и ее потенциал
Согласно закону всемирного тяготения, две точечные или сферические массы m1 и m2, расположенные на расстоянии r, притягиваются взаимно с силой
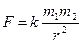 , (2.1)
, (2.1)
где k – гравитационная постоянная, равная 6,673 10-8 см3/(г с2) в системе СГС или 6,673 10-11 м3/(кг с2). Как это видно из приведенной формулы, сила взаимного притяжения двух масс имеет размерность г см/с2 = дин в системе СГС или кг м/с2 = Ньютон в системе СИ.
Если в пространстве действуют силы, значит, должна быть энергия. Основной скалярной характеристикой поля притяжения является потенциал, который определяется как энергия (или работа) по перемещению единичной точечной массы из бесконечности в данную точку поля. В гравиразведке обычно потенциал обозначается буквами V или W. В дальнейшем мы будем означать гравитационный потенциал буквой V.
Сила притяжения, действующая на единичную точечную массу (m1 = 1, m2 = m), численно равна напряженности поля притяжения или ускорению, сообщаемому этой массе:
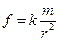 . (2.2)
. (2.2)
Отсюда видно, что сила ньютоновского притяжения (2.1) отличается от ускорения (напряженности 2.2) размерностью (см/с2 в системе СГС или м/с2 в системе СИ), хотя для краткости ее часто называют силой притяжения. Напряженность определяется как градиент потенциала f = -grad V, где:
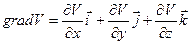 . (2.3)
. (2.3)
Для точечных и сферических масс 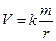 (2.4)
(2.4)
Если взять прямоугольную систему координат с точкой измерения в ее центре, расположив притягивающую массу в произвольной точке, то сила f будет направлена к центру притягивающей массы (рис. 2.1.). Спроецируем силу f на оси координат и обозначим углы между силой f и осями Х, Y, Z соответственно 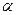 ,
, 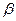 ,
, 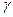 . Тогда составляющие напряженности определятся, как
. Тогда составляющие напряженности определятся, как
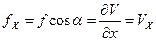 ,
, 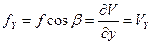 ,
, 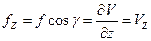 . (2.5)
. (2.5)
С учетом того, что 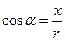 ,
, 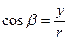 ,
, 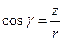 , можно записать:
, можно записать:
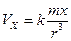
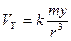
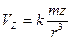 . (2.6)
. (2.6)
Силу можно определить через составляющие, как 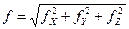 (2.7)
(2.7)
Или, если обозначить ее через потенциал: 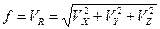 . (2.8)
. (2.8)
Для произвольных масс потенциал, напряженность поля и ее составляющие запишутся в виде объемных интегралов (плотность объекта 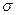 считаем постоянной):
считаем постоянной):
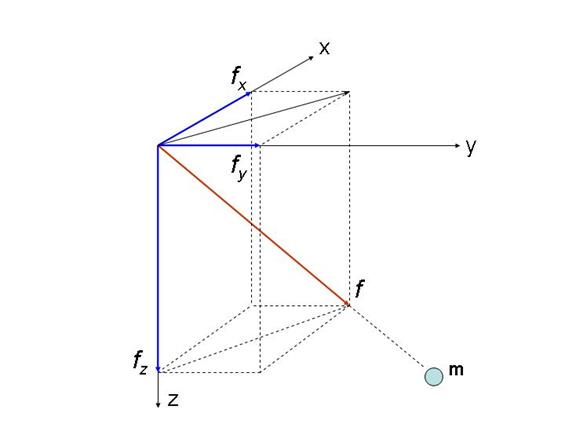
Рис. 2.1. Составляющие силы притяжения.
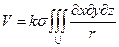 ,
, 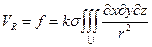 , (2.9)
, (2.9)
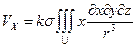
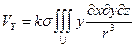
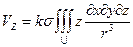 . (2.10)
. (2.10)
Таким образом, потенциал притяжения – это такая функция, первые производные которой равны проекциям напряженности силы притяжения на эти оси. Это справедливо и для тел произвольной формы.
Потенциал силы притяжения обладает следующими свойствами
- При перемещении точки в направлении, перпендикулярном действию силы, потенциал остается постоянным (уровенная или эквипотенциальная поверхность)
- При перемещении массы по замкнутому контуру работа равна нулю
- При перемещении точки вдоль действия силы f на расстояние dS приращение потенциала определяется, как произведение силы на расстояние: dV = f *dS (теорема Брунса)
- Вне возмущающих масс действует уравнение Лапласа
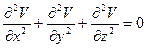 |
(2.11)
- Внутри возмущающих масс действует уравнение Пуассона
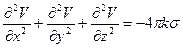 |
(2.12)
Дата добавления: 2015-06-27; просмотров: 3500;
