Гравитационное поле вертикального стержня

Некоторые небольшие по диаметру и уходящие на большую глубину интрузии могут быть аппроксимированы вертикальным стержнем или цилиндром (рис.28).

Массу стержня можно представить в виде суммы элементарных масс, распределенных по всей длине стержня. Полагая 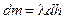, где l – линейная плотность стержня, получим:

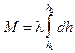. (V.15)

Потенциал стержня можно представить в виде потенциала точечной массы:

.

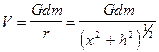Найдем вертикальную составляющую силы тяжести Dg элементар­ной массы стер­жня dm.

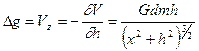. (V.16)

Для нахождения поля силы тяжести, созданного всей массой стержня, полученное выражение (V.16) проинтегрируем в пределах от h₁ до h₂:

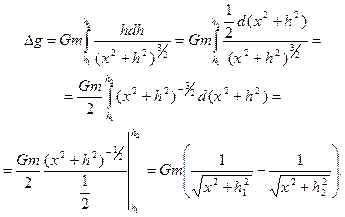(V.17)

Для стержня бесконечной длины (h₂ ® ¥):

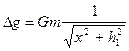. (V.18)

Дифференцируя (V.18) по x, найдем V_xz:

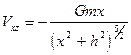. (V.19)

При x = 0

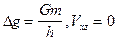. (V.20)

Графики Dg и V_zx показаны на рис. 28. Сравнивая их с аналогичными графиками для шара, нетрудно убедиться в сходстве полей Dg и V_zx для шара и вертикального стержня. В плане поле стержня также имеет вид концентрических окружностей более или менее правильной формы, сходящихся над вертикальной осью стержня (рис. 28).