Гравитационное поле Земли и его элементы

Г.П.З.,стр17-18поле силы тяжести; силовое поле, обусловленное притяжением (тяготением) Земли и центробежной силой, вызванной её суточным вращением. Зависит также (незначительно) от притяжения Луны, Солнца и др. небесных тел и масс земной атмосферы. Гравитационное поле Земли характеризуется силой тяжести (F_т; Р=F_пр+F_цб), потенциалом силы тяжести и различными производными от него. Потенциал имеет размерность см².сек^–2. За единицу измерения первых производных потенциала, в том числе силы тяжести, в гравиметрии принимается миллигал (мгл), равный 10^–3 см.сек^-2, а вторых производных — этвеш (Е), равный 10^–9 сек^–2, кот. характеризует изменение силы тяжести на 0,1 мГал на расстоянии 1 км. Часть потенциала силы тяжести, обусловленная только притяжением масс Земли, называется потенциалом земного притяжения, или геопотенциалом. Потенциал силы тяжести используется при изучении фигуры Земли, близкой к уровенной поверхности Г.П.З. (уровенной называется поверхность, во всех точках которой потенциал имеет одинаковое значение; сила тяжести направлена к ней по нормали). Одна из уровенных поверхностей, которая совпадает с невозмущённой средней поверхностью океанов, называется геоидом.

F=G*m₁m₂/r²

G-гравитационная постоянная =66,7*10^-12м³/(кг*с²); По физическому смыслу гравитационная постоянная-сила, действующая между двумя единичными массами, находящимися на расстоянии одного метра; m₁-масса Земли; m₂-масса другого тела; в предположении, что r = 1 м. Сила тяжести и сила притяжения, различные понятия. На полюсе сила тяжести больше, чем на экваторе.

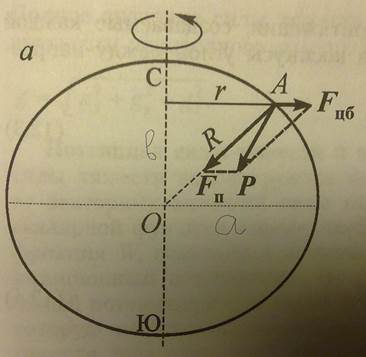
На рисунке представлены составляющие силы тяжести, где Fцб – центробежная сила, возникающая в результате вращения Земли вокруг своей оси, направлена по нормали r к оси вращения и равна: Fцб=ω²r=v²/r, где ω=2πТ-угловая скорость вращения (Т-период вращения Земли); r-расстояние от точки А до оси вращения,

v= ωr-линейная скорость на поверхности Земли. Период вращения Земли (астрономические сутки) составляет Т=86164 с, линейная скорость вращения максимальна на экваторе (v_э =460 м/с) и равна нулю на географических полюсах. Р-сила тяжести, на поверхности в точке А представляет равнодействующую двух сил-силы притяжения и центробежной силы. Р= Fп+ Fцб; Fп-сила притяжения между двумя точечными массами, находящимися на расстоянии R.

2. Сила тяжести и ее составляющие.стр 7, 12, 13Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. Это основная величина измеряемая в гравиразведке. Действие силы тяжести проявля­ется в том, что тело единичной массы m=1 притягивается Землей с силой P = mg,где g —ускорение свободного падения.Сила Р представляет равнодействующую силы притяжения Fп и центробежной силы Fц , т. е. Р = Fп + Fц, где мacca Земли М = 5,974*10²⁴ кг, полярный ра­диус b = 6357 км, экваториальный ра­диус а = 6378 км, коэффициент сжатия а =(а— b)/а= 1/298,25, средний радиус Земли R =6,371 км. На рисунке представлены составляющие силы тяжести, где Fцб – центробежная сила, возникающая в результате вращения Земли вокруг своей оси, направлена по нормали r к оси вращения и равна: Fцб=ω²r=v²/r, где ω=2πТ-угловая скорость вращения (Т-период вращения Земли); r-расстояние от точки А до оси вращения,

v= ωr-линейная скорость на поверхности Земли. Период вращения Земли (астрономические сутки) составляет Т=86164 с, линейная скорость вращения максимальна на экваторе (v_э =460 м/с) и равна нулю на географических полюсах. Р-сила тяжести, на поверхности в точке А представляет равнодействующую двух сил-силы притяжения и центробежной силы. Р= Fп+ Fцб; Fп-сила притяжения между двумя точечными массами, находящимися на расстоянии R.

Как видно на рис, в общем случае сила тяжести не направлена точно к центру Земли, отклонение зависит прежде всего от величины центробежной силы.

По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести F_т=GMm/R² ,где М - масса Земли; R - радиус Земли.
Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле F_т=GMm/R² модуль ускорения свободного падения g находят по формуле g=F_т/m=GM/R². Из формулы g=F_т/m=GM/R² следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы g=F_т/m=GM/R² следует, что Fт = mg. В векторном виде F_т=mg . Поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы F_т=GMm/R² видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе. Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела.

Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле

g=GM/(R+h) 2.

3. Сила притяжения и ее потенциал.стр 8-11Сила притяжения F_п , действующая между двумя массами, вычисляется согласно закону гравитационного притяжения Ньютона и направлена приблизи­тельно к центру Земли. Для точечных масс m₁ и m₂, находящихся друг от друга на расстоянии r (r=1м), сила притяжения F_п=Gm₁*m₂/p² и направлена по прямой, соединяющей эти массы. Константа G наз-ся гравитационной постоянной. G=6,67*10^-11 м3/кг*с2. За точечные массы можно принять только однородные или однородно-слоистые сферы конечных размеров, во всех других случаях размеры масс должны быть бесконечно малы по срав­нению с расстояниями между их центрами. Естественно, что земной сфероид за точечную массу принять нельзя. Для вычис­ления силы притяжения земного сфероида его необходимо раз­бить на массы бесконечно малых объемов dQ (точечные массы). Притяжение всего земного сфероида равно интегральной сумме притяжений каждой из помещенных внутри его точечных масс. Но мы не можем просумми­ровать арифметически полученные результаты, поскольку направления действия эле­ментарных сил притяжения разных точечных масс оказываются различными. Такое суммирование можно выполнять только раз­дельно для составляющих силы притяжения по осям х, у, z. Функция V(x,y,z) обладает свойством, что ее производные по x,y,z равны составляющим силы притяжения по соответствующим осям координат, называется потенциалом притяжения.Частная производная от потенциала притяжения по любому произвольному направлению s равна проекции силы притяжения на это направление:

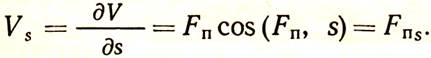
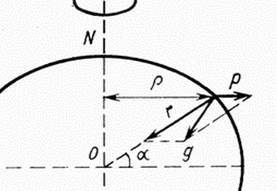
В качестве примера притяжения масс в пространстве рассмотрим рисунок, где Р-произвольная точка находящаяся на поверхности земного сфероида, начало координат в центре Земли, ось z совмещена с осью вращения, а оси х, у находятся в плоскости экватора. Согласно закону Ньютона, если одну из точечных масс в точке Р на поверхности земного сфероида считать единичной массой, то другая точечная масса dm, представляющая совокупность масс Земли с постоянной плотностью, будет притягивать эту единичную массу с силой dF=Gdm/ρ², где ρ-расстояние между точечными массами. Итак, dm-точечная масса -координаты её центра.

4. Сила тяжести и ее потенциал.стр 13-14Силой тяжести ( ) называют равнодействующую двух сил - силы ньютоновского притяжения всей массой Земли ( ) и центробежной силы, возникающей вследствие суточного вращения Земли ( ). Отнесенные к единице массы, эти силы характеризуются ускорениями силы тяжести g=F/m, ньютоновского притяжения f=F_н/m и центробежным P=P/m. Ускорение силы тяжести равно геометрической сумме ускорения притяжения и центробежного ускорения.Сила притяжения какой-либо массы ( 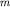) всей массой Земли ( ) определяется законом всемирного тяготения Ньютона: F=G*m₁m₂/r² Где r- расстояние между центрами масс m и M, т.е. радиус Земли; g - гравитационная постоянная, равная G=6,67*10^-11 м³/кг*с². Величина P изменяется от нуля на полюсе (R=0) до максимума на экваторе. сила тяжести почти целиком определяется силой притяжения. Разная величина радиуса Земли на полюсе и экваторе наряду с изменением центробежной силы приводит к увеличению g на полюсе по сравнению с g на экваторе.

.Потенциал силы тяж (W) -это интегральная функция, которая является мерой энергии затрачиваемой на перемещение единичной массы из каждой точки поля в бесконечность. g=-dW/dr, т.е. сила тяжести есть производная потенциала силы тяжести по направлению к центру Земли. Поэтому гравитационное поле можно представить в виде набора бесконечного числа поверхностей, на которых потенциал остается постоянным, а ускорение силы тяжести направлено перпендикулярно этой поверхности. Такие поверхности называют эквипотенциальными или уровенными. У Земли есть одна уровенная поверхность, которая совпадает с невозмущенной волнениями поверхностью океанов. Она называется геоидом. геоид - это условная уровенная поверхность, которая совпадает со средним уровнем океанов и открытых морей, проходит под сушей и по определению везде горизонтальна, а ускорение силы тяжести к ней перпендикулярно.

сила тяжести представ­ляет геометрическую сумму силы притяжения и центробежной силы, ее проекции на оси координат

Wх = Vх+ Uх, Wу = Vу+ Uу, W z = V z (Uz=0), где

W = V+ U

На уровенной поверхности действует только нормальная (вертикальная) составляющая силы тяжести и не действуют горизонтальные составляющие.

Сила тяжести, в отличие от потенциала силы тяжести, в различных точках уроненной поверхности не одна и та же, а только направлена к ней по нормали.

5. Вторые производные потенциала силы тяжести, их физический смысл и геологоразведочное значение. Производные потенциала силы тяжести по трем координатным осям g_x=∂W/∂x; g_y=∂W/∂y; g_z=∂W/∂z; однозначно определяют его полный вектор. В частности, если ось z направить к центру Земли, то ∂W/∂x=∂W/∂y=0; а g=∂W/∂x. В гравиметрии кроме первых производных изучаются вторые производные потенциала или их разности: ∂²W/∂x∂y; ∂²W/∂x∂z; ∂²W/∂y∂z; ∂²W/∂x²; ∂²W/∂y²; ∂²W/∂z²; ∂²W/∂x² – ∂²W/∂y². Те производные, кот имеют dz, наз. Градиентами сил тяжести и применяются для разведочных целей в гравиразведке; Остальные прим-ся для изучения фигуры (формы) Земли. Фигуру земли можно изучать только по гравитационному полю. Физический смысл этих выражений легко получить, если иметь в виду, что g=∂W/∂z. Так вторая производная ∂²W/∂x∂z=∂g/∂x указывает на скорость изменения силы тяжести по оси х, т.е. является гори-зонтальным градиентом силы тяжести. Полный горизонтальный градиент силы тяжести это квадратный корень из W_г=W²_xz+W²_yz Аналогичный смысл имеют вторые производные ∂²W/∂x∂z и ∂²W/∂z²

Практической единицей измерения градиента силы тяжести принимается 1 этвеш(Е), что соответствует изменению силы тяжести в 0,1 мГал на 1 км. Вторые производные потенциала силы тяжести применяются при решении геологоразведочных и геодезических задач. Аномальная часть вторых произ-водных потенциала позволяет судить о плотностных неоднородностях в верхних частях земной коры.

6. Нормальные значения силы тяжести. Стр18 Нормальным значением силы тяжести (γ₀) называется сила тяжести, обусловленная суточным вращением и притяжением Земли, в предположении, что она состоит из однородных по плотности концентрических слоев. Принимая Землю за сфероид, Клеро получил следующую приближенную формулу для ее расчета: γ= γ _э(1+βsin²φ), где γ _э- сила тяжести на экваторе; φ- географическая широта пункта наблюдения; β- коэффициент, зависящий от угловой скорости вращения и сжатия сфероида. Коэффициент β ~ 1/189 характеризует относительное увели­чение силы тяжести у полюсов по сравнению с ее значением на экваторе. Формула Клеро отражает распределение силы тяжести на поверхности Земли лишь в грубом приближении. Ее нельзя использовать при вычислении аномалий силы тяжести, по­скольку допущенные при этом погрешности значительно превос­ходят величину аномалий, создаваемых изучаемыми геологиче­скими структурами. Поэтому в гравиразведке используется более точная формула, которая дает распределение силы тяже­сти на поверхности однородного земного сфероида и нормальные значения силы тяжести для его поверхности рассчитываются по формуле:гамаγ= γ _э(1+β₁sin²φ- β₂sin²2φ)-формула нормального значения силы тяжести; Коэффициенты β, β₁ зависят от формы Земли, ее угловой скорости вращения, распределения масс. Имеется несколько вариантов формулы нормального значе­ния силы тяжести, которые отличаются друг от друга значе­ниями коэффициентов γ _э, β_{1 и} β₂

Коэффициенты по формуле Гельмерта(мГал)

γ _э 978030

β₁ 0, 005302

β₂ 0,000007

Коэффициенты по формуле Кассиниса (в мГал)

γ _э 978049

β₁ 0, 0052884

β₂ 0,0000059

Коэффициенты разные, так как наблюдается расхождение в зависимости от широты.

7. Редукции и аномалии силы тяжести.В наблюденные значения силы тяжести вводятся поправки (редукции). Введение поправок необходимо потому, что нормальные значения относятся к поверхности геоида, которая совпадает с уровнем океана, а измеренные значения относятся к действительной (реальной) земной поверхности. Для того, чтобы все наблюдения силы тяжести были сопоставимы, их приводят к одной поверхности - уровню геоида, т.е. как бы опускают точку наблюдения на этот уровень. Это осуществляется путем введения поправок за высоту, за притяжение промежуточного слоя и окружающий рельеф. Поправки называются редукциями. Основными из них являются: поправка за высоту, за притяжение промежуточного слоя, за рельеф. Для приведения измеренного значения g_н к уровню океана вводят поправку за высоту(∆g). Эту поправку называют поправкой за "свободный воздух" или поправкой Фая. Эта поправка должна прибавляться к измеренной силе тяжести, если точка наблюдений находится выше уровня геоида, и вычитаться, если ниже. При введении поправки за притяжение промежуточного слоя (∆g₂) вычисляется притяжение масс слоем между уровнем океана и данной точкой. Для учета бокового притяжения рельефа местности, окружающего пункт наблюдения, при съемке в горных районах вводятся топографические поправки (∆g₃). В геодезической гравиметрии под аномалией силы тяжести понимают разность между наблюденным значением (g_н) и нормальным (γ₀) с учетом поправки Фая, она рассчитывается по формуле ∆g_ф~g_н-γ₀+g₁ и называется аномалией Фая. Основной аномалией в гравиразведке является аномалия Буге: ∆g_Б=g_н-γ₀+ ∆g₁+ ∆g₂+∆g₃= g_н-g_теор; в которую вводятся все поправки.

К вычислению поправок за высоту и промежуточный слой представлен рисунок, где g_н –наблюденное значение поля, σ- плотность слоя лежащего над уровнем моря, верхняя граница которого определяется рельефом местности, а точка наблюдений на поверхности находится на высоте h относительно уровня моря .Для вычисления аномалий силы тяжести нужно, чтобы нормальное поле силы тяжести соответствовало уровню пункта наблюдений и условиям наблюдения. Поэтому в нормальные значения силы тяжести ɤ вводится поправка или редукция за высоту точки наблюдения, снимающая эти расхождения и приводящая вычисленные нормальные значения к уровню пункта наблюдений, а из наблюдённого значения поля g_н вычитают влияние масс, залегающих выше уровня моря.

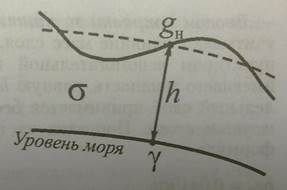
8. Аномалии силы тяжести Бугэ.стр 21 Суммарная поправка за высоту, промежуточный слой и рельеф на­зывается поправкой Буге,при наблюдениях выше уровня моря она будет равна:

Выражение для аномального значения силы тяжести, получило название аномалии Буге:

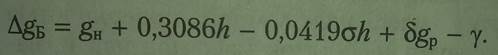
Аномалию Буге обязательно используют при гравиразведочных работах.

Профили и карты аномалий силы тяжести в редукции Буге являются основным материалом для последующей интерпретации гравиразведочных данных.

аномалия Буге: ∆g_Б=g_н-γ₀+ ∆g₁+ ∆g₂+∆g₃= g_н-g_теор; в которую вводятся все поправки. Под g_теор понимается суммарная поправка в наблюденные значения, которая может быть определена до проведения работ, поскольку в ней имеются лишь топографические координаты точек наблюдения (φ,Н). Ее рассчитывают с помощью ЭВМ. При вычислении аномалий Буге следует различать два случая: 1) точка наблюдения расположена на суше; 2) точка наблюдения расположена на море. В первом случае для точек 1, 2, 5, 6, расположенных на суше, аномалия Буге вычисляется по формуле: Для точек 3 и 4, расположенных на море, поправка за влияние промежуточного слоя вычисляется по формуле: Аномалия Буге в этом случае вычисляется по формулам 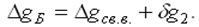с учетом 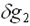, вычисленной по формуле

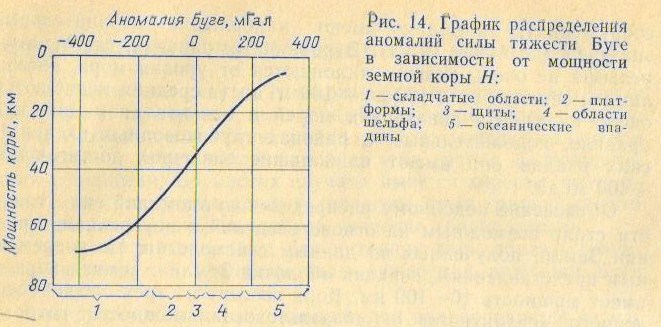
9. Геологические факторы, формирующие аномалии Буге.стр 25Аномалию Буге вычисляют как разность между наблюденным и нормальным значениями силы тяжести с введением суммарной поправки за высоту, промежуточный слой и рельеф. При наблюдениях выше уровня моря она будет равна:

Выражение для аномального значения силы тяжести, получило название аномалии Буге:

После вычитания из наблюденного поля нормального значения силы тяжести и поправки Буге оставшаяся его часть-аномалия силы тяжести- характеризует влияние залегающих внутри Земли плотностных неоднородностей. Изучив распределение аномалий на поверхности Земли, можно получить информацию о ее внутреннем строении. Большую роль при вычислении аномалии Буге играет выбор плотности промежуточного слоя: если плотность принять слишком малой, то возможна прямая корреляционная зависимость значений аномалий от рельефа физической поверхности; если же плотность слоя сильно завышена, то будет наблюдаться отрицательная корреляционная зависимость. При вычислении аномалий силы тяжести за одно из значений плотности промежуточного слоя берут среднее значение плотности земной коры-2,67 г/см³. Для геологической интерпретации рекомендуется вычислять аномалии Буге с истинной (реальной) плотностью промежуточного слоя, полученной в условиях естественного залегания горных пород. Местоположение на местности контуров нуле-ных значений аномалий Буге зависит от того, по какой фор­муле были вычислены нормальные значения силы тяжести (Гельмерта или Кассиниса), а также от значения плотности промежуточного слоя в поправке Буге.

10. Способы трансформации гравитационного поля и их сущность.стр55-56 Наблюденное гравитационное поле представляет сумму аномалий, созданных различными возмущающими массами: , где ∆_kg_a – аномалия, обусловленная одной из возмущающих масс. Для обнаружения в суммарном гравитационном поле аномалии от интересующей геологической структуры нужно, чтобы ее интенсивность преобладала над интенсивностью аномалий от всех других возмущающих масс. Решение подобной задачи возможно только в том случае, если аномалии различаются по своим свойствам, что может быть вызвано различными глубинами залегания и формами возмущающих масс и другими особенностями. Операции по разделению гравитационных аномалий можно разделить на 3 класса: 1. аналитическое продолжение наблюденного поля аномалий. Трансформации основаны на том, что аномалии от мелких и неглубоко залегающих объектов при пересчете поля вверх сглаживаются быстрее, чем аномалии от крупных и относительно глубоко залегающих масс, и наоборот: при пересчете поля вниз, аномалия начинает лучше соответствовать форме объекта, в то время как для удаленных объектов аномалии продолжают оставаться нечеткими. Примером служит задача перевычисления аномалий силы тяжести в верхнее полупространство на новый уровень z₀ сводится к вычислению интеграла Пуассона:

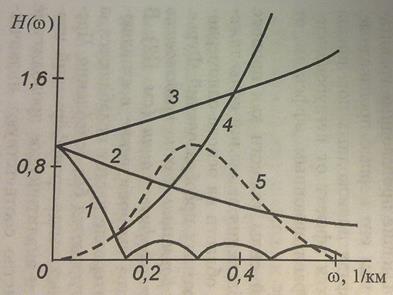
2. Усреднение аномального поля. Используется для нахождения региональных аномалий. Осуществляется с помощью усреднения значений ∆g_a на некотором участке. 3. Вычисление высших производных потенциала силы тяжести (вертикальных и горизонтальных). Применение высших производных потенциала силы притяжения позволяет в ряде случаев выявить локальные аномалии, обусловленные малоамплитудными структурами в осадочной толще, а при благоприятных условиях – и крупные нефтегазовые залежи.

Рисунок отображает частотные характеристики различных трансформаций гравитационного поля, где 1 - усреднения; 2- аналитического продолжения в верхнее полупространство; 3 - аналитического продолжения в нижнее полупространство; 4 - вычисления высших производных; 5- аналитического продолжения высших производных в верхнее полупространство.

11. Качественная и количественная интерпретация данных гравиразведки.стр52-55 Качественная интерпретация. Интерпретация данных гравиразведки подразделяется на качественную и количественную. Первым этапом интерпретации результатов гравиразведки является качественная интерпретация.

Качественная интерпретация заключается в анализе особен­ностей наблюденного аномального поля, в результате которого получают сведения об источниках аномалий. Она основана на применении метода аналогий и сопоставлении данных гравиразведки с другими геофизическими методами и бурением. По результатам качественной интерпретации составляют схему рас­пределения аномалий силы тяжести, которую затем используют дли тектонического районирования изучаемого района. При качественной интерпретации дается визуальное описание характера аномалий силы тяжести по картам и профилям, т.е. отклонений от средних (фоновых) значений ∆g_Б. Устанавливается связь гравитационных аномалий с геологическим строением, выделяются региональные аномалии, связанные со строением земной коры и локальные. Региональные обусловлены крупными поднятиями и прогибами земной коры, а так же неоднородными по петрографическому составу блоками кристаллического фундамента. Локальные аномалии, часто представляющие большой разведочный интерес, располагаются в пределах региональных аномальных зон и нередко связаны с локальными структурами в осадочном чехле или с зонами тектонических нарушений. Выделение региональных аномалий от локальных называется снятием регионального фона. Оно производится, как правило, графическим путем.

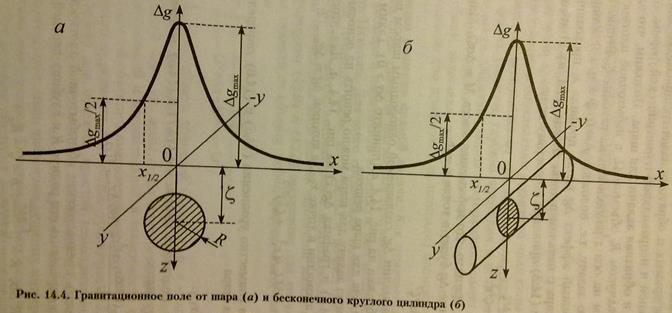
Количественная интерпретация. Количественная интерпретация данных гравиразведки за­ключается в решении прямой и обратной задач. Общие положения. Определение глубины, формы, размеров и точного местоположения геологических тел, создающих наблюденные аномалии, составляет основную цель количественной (расчетной) интерпретации, основанной на методах решения обратной задачи гравиразведки. Решение обратной задачи неоднозначно, так как одинаковые аномалии силы тяжести могут быть созданы геологическими объектами разной формы, размеров и плотности. Методы решения обратной задачи гравиразведки принято подразделять на прямые, в которых элементы залегания гравитирующих масс определяются непосредственно по картам и графикам (или вторых производных потенциала), и косвенные, когда наблюденные аномалии сравниваются с набором теоретически рассчитанных аномалий над определенными объектами, и методом последовательных приближений добиваются наилучшего совпадения полей. Прямая и обратная задачи могут решаться для шара, для горизонтального круглого цилиндра, для вертикальной ступени, для контактной поверхности, для объектов произвольной формы.