Солнце. Основные характеристики
ЧАСТЬ I
Глава I. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
Планеты и законы их обращения
Солнечная система включает девять крупных планет, которые со своими 57 спутниками обращаются вокруг массивной звезды по эллиптическим орбитам (рис. 1). По своим размерам и массе планеты можно разделить на две группы – планеты земной группы, расположенные ближе к Солнцу, – Меркурий, Венера, Земля и Марс и планеты-гиганты – Юпитер, Сатурн, Уран и Нептун, находящиеся на значительно более удаленных орбитах от центральной звезды. Последняя из известных планет Плутон своей орбитой с радиусом около 6 млрд. км очерчивает границы Солнечной системы. Плутон не относится к планетам-гигантам, его масса почти в десять раз меньше массы Земли. Аномальные характеристики этой крошечной планеты позволяют рассматривать ее как бывший спутник Нептуна.
Кроме больших планет между орбитами Марса и Юпитера вращается более 2300 малых планет – астероидов, множество более мелких тел – метеоритов и метеорной пыли, а также несколько десятков тысяч комет, двигающихся по сильно вытянутым орбитам, некоторые из которых далеко выходят за границы Солнечной системы.
Все планеты и астероиды обращаются вокруг Солнца в направлении движения Земли – с запада на восток. Это так называемое прямое движение. Основные закономерности движения планет полностью определяются законами Кеплера. Рассмотрим эти законы и охарактеризуем основные элементы эллиптических орбит.
Согласно первому закону, все планеты обращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. На рис. 2 показаны элементы планетных орбит с Солнцем (С) в фокусе. Линия АП называется линией апсид, крайние точки которой афелий (А) и перигелий (П) характеризуют наибольшее и наименьшее удаление от Солнца. Расстояние планет (Р) на орбите от Солнца (гелиоцентрическое расстояние) определяется радиусом-вектором r = СР. Отношение полуфокального расстояния (с) к большой полуоси (а) называется эксцентриситетом орбиты:
Рис. 1. Солнечная система
| Рис. 2. Элементы планетной орбиты: АП – большая полуось орбиты, ось апсид; П – перигелий; А – афелий; r – радиус вектор |
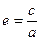 . (I.1)
. (I.1)
Если обозначить через q перигельное расстояние, а через Q афелийное расстояние, то их значения легко определить из выражений:
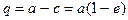 ; (I.2)
; (I.2)
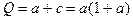 . (I.3)
. (I.3)
Тогда, определив большую полуось (а), мы найдем среднее годичное расстояние планеты до Солнца:
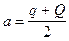 . (I.4)
. (I.4)
| Рис. 3. Площади, описываемые радиус-вектором планеты |
Cреднее гелиоцентрическое расстояние Земли от Солнца равно 149,6 млн. км. Эта величина называется астрономической единицей и принимается за единицу измерений расстояний в пределах Солнечной системы.
Согласно второму закону Кеплера радиус-вектор планеты описывает площади, прямо пропорциональные промежуткам времени. Если обозначить через S1 площадь перигелийного сектора (рис. 3), а через S2 – площадь афелийного сектора, то их отношение будет пропорционально временам Dt1 и Dt2,за которые планета прошла соответствующие отрезки дуг орбиты:
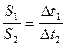 . (I.5)
. (I.5)
Отсюда следует, что секториальная скорость
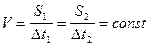 (I.6)
(I.6)
величина постоянная.
Время, в течение которого планета сделает полный оборот по орбите, называется звездным, или сидерическим периодом Т (рис. 3). За полный оборот радиус-вектор планеты опишет площадь эллипса:
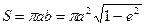 . (I.7)
. (I.7)
Поэтому секториальная скорость
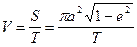 (I.8)
(I.8)
оказывается наибольшей в перигелии, а наименьшей – в афелии. Используя второй закон, можно вычислить эксцентриситет земной орбиты по наибольшему и наименьшему суточному смещению Солнца по эклиптике, отражающему движение Земли (см. §4). Земля в перигелии пребывает в начале января (hmax = 61'), а в афелии в начале июля (hmax = 57'). По второму закону Кеплера скорость Земли в афелии и перигелии определяется из выражений:
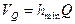 ;
; 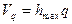 . (I.9)
. (I.9)
Учитывая закон сохранения момента количества движения
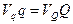 (I.10)
(I.10)
и подставив сюда значения (I.9) с учетом выражений (I.2) и (I.3), найдем:
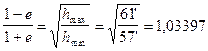 , откуда е = 0,0167.
, откуда е = 0,0167.
Таким образом, орбита Земли лишь ненамного отличается от окружности.
Согласно третьему закону Кеплера, квадраты сидерических периодов обращения планет (Т12 и Т22) прямо пропорциональны кубам их средних расстояний от Солнца (а13 и а23):
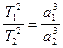 . (I.11)
. (I.11)
Если одна из планет, к примеру, Земля, и период ее сидерического обращения Т1 и расстояние от Солнца а1 положить равным единице, т.е. а1 = 1 а. е., Т1 = 1 году, то выражение (I.11) принимает простой вид:
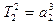 . (1.12)
. (1.12)
Полученное выражение позволяет, по известным из наблюдений периодам обращения планет, других небесных тел вокруг Солнца, вычислять их средние гелиоцентрические расстояния.
Найденные эмпирически из наблюдательной астрономии законы Кеплера показали, что Солнечная система представляет собой механическую систему с центром, находящимся в солнечной массе.
Законы Кеплера послужили Ньютону основой для вывода своего знаменитого закона всемирного тяготения, который он сформулировал так: каждые две материальные частицы взаимно притягиваются с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
Математическая формулировка этого закона имеет вид:
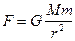 , (I.13)
, (I.13)
где M и m – взаимодействующие массы, r – расстояние между ними; G – гравитационная постоянная. В системе СИ G = 6,672·10-11 м3·кг-1·с-2. Физический смысл гравитационной постоянной заключается в следующем: она характеризует силу притяжения двух масс весом в 1 кг каждая на расстоянии в 1 м. Величина G впервые была определена в 1798 г. английским физиком Кавендишем с помощью крутильных весов.
Закон Ньютона решил задачу о характере действия силы, управляющей движением планет. Это сила тяготения, создаваемая центральной массой Солнца. Именно эта сила не дает планетам разлететься, а сохраняет их в связной системе последовательных орбит, по которым как на привязи сотни миллионов лет кружатся большие и малые планеты.
Решая задачу движения двух тел под действием взаимного притяжения Ньютон аналитически определил законы движения планет в поле тяготения Солнца. Тем самым эмпирические законы Кеплера получили строгое математическое доказательство. Третий же закон был уточнен за счет введения масс планет и Солнца:
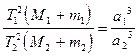 . (I.14)
. (I.14)
Теперь с его помощью оказалось возможным вычислять массы небесных тел. Полагая в выражении (I.14) массы спутников планет m1 и m2равными нулю, ввиду их малости в сравнении с массой планет (за исключением Луны) и приняв массу Земли M2 = 1, соотношение (I.14) примет вид:
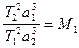 . (I.15)
. (I.15)
Воспользуемся законом тяготения и определим массу Земли, полагая, что взаимодействуют две массы – Земли (М)и некоторого тела, лежащего на ее поверхности. Сила притяжения этого тела определяется законом Ньютона:
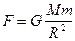 . (I.16)
. (I.16)
Но одновременно из второго закона механики эта же сила равна произведению массы на ускорение:
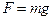 , (I.17)
, (I.17)
где g – ускорение силы тяжести; R – радиус Земли.
Приравнивая правые части выражений (I.16) и (I.17):
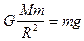 ,
,
найдем выражение для определения массы Земли:
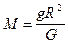 . (I.18)
. (I.18)
Подставив в (I.18) известные значения G = 6,672·10-11 м3·кг-1·с-2,
g = 9,81 м/с2, R = 6,371·106 м, в итоге получим MЗ = 5,97·1024 кг, или в граммах: M3 = 5,97·1027 г. Такова масса Земли. Обращаем внимание на формулы (I.16), (I.17), (I.18) – их надо твердо помнить. В дальнейшем мы часто будем пользоваться ими как исходными для определения входящих в них параметров.
Теперь воспользуемся уточненным третьим законом Кеплера и найдем из выражения (I.15) массу Солнца. Для этого рассмотрим две системы тел – Солнце с Землей и Землю с Луной. В первой системе
a1 = 149,6·106 км, Т1 = 365,26 суток; во второй системе а2 = 384,4·103 км, Т2 = 27,32 суток. Подставляя эти значения в формулу (I.15), находим массу Солнца в относительных единицах массы Земли М0=328700 М3.Полученный результат отличается от более точных расчетов, так как в сравнении с массой Земли массу Луны нельзя приравнивать нулю (масса Луны составляет 1/81 массы Земли). Зная массу Земли в абсолютных единицах (килограммах или граммах) и взяв более точное определение массы Солнца (М0 = 333000 М3), определим его абсолютную массу: М0 = 333000·5,97·1027 г = 1,98·1033 г.
В настоящее время для более точного определения массы и фигуры планет и их спутников используются параметры орбиты искусственных спутников, запускаемых с Земли.
Дальше мы увидим, что закон тяготения Ньютона объясняет не только движение системы планет и других космических объектов в Солнечной системе, но и лежит в основе понимания процессов, происходящих внутри самих астрономических масс.
§2. Орбитальные характеристики планет
Физические условия на поверхности каждой из девяти планет всецело определяются их положением на орбите относительно Солнца. Ближайшие к светилу четыре планеты – Меркурий, Венера, Земля и Марс – имеют сравнительно небольшие массы, заметное сходство в составе слагающего их вещества и получают большое количество солнечного тепла, ощутимо влияющего на температуру поверхности планет. Две из них – Венера и Земля – имеют плотную атмосферу, Меркурий и Марс атмосферы практически не имеют.
Планеты-гиганты Юпитер, Сатурн, Уран и Нептун значительно удалены от Солнца, имеют гигантские массы и плотную мощную атмосферу. Все они отличаются высокой осевой скоростью вращения. Солнечное тепло почти не достигает этих планет. На Юпитере оно составляет 0,018·103 Вт/м2, на Нептуне – 0,008·103 Вт/м2.
Все планеты, за исключением Меркурия и Венеры, имеют спутники, общее число известных на сегодняшний день достигает 57. Наибольшее количество спутников имеют Юпитер – 16, Сатурн – 17 и Уран – 15. Остальные планеты имеют один – два спутника.
Большая часть массы вещества Солнечной системы сосредоточена в самом Солнце – более 99%. На долю планет приходится менее 1% общей массы. Остальное вещество рассеяно в астероидах, кометах, метеоритах, метеорной и космической пыли.
Все планеты имеют сравнительно небольшие размеры и в сравнении с расстояниями между ними их можно представлять в виде материальной точки. Из курса физики известно, что произведение массы тела на его скорость называется импульсом:
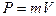 , (I.19)
, (I.19)
а произведение радиуса-вектора на импульс – моментом импульса:
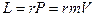 . (I.20)
. (I.20)
Из приведенного выражения видно, что скорость V движения планеты по эллиптической орбите меняется вместе с изменением радиуса-вектора r. При этом на основании второго закона Кеплера имеет место сохранение моментов импульса:
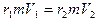 . (I.21)
. (I.21)
Из (I.21) видно, что при увеличении r1 скорость V1должна уменьшаться, и наоборот (масса т планеты неизменна). Если выразить линейную скорость V через угловую скорость w
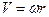 , (I.22)
, (I.22)
то выражение для момента импульса планеты примет вид:
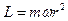 . (I.23)
. (I.23)
Из последней формулы следует, что при сжатии вращающихся систем, т. е. при уменьшении r и постоянстве т,угловая скорость вращения w неизбежно возрастает.
В табл. I.1 приведены орбитальные параметры планет. Хорошо видно, как по мере возрастания радиуса орбиты (гелиоцентрического расстояния) уменьшается период обращения и, следовательно, скорость движения планет.
При движении планеты вокруг Солнца сила притяжения последнего уравнивается центростремительной силой, приложенной к планете:
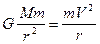 . (I.24)
. (I.24)
Отсюда легко найти среднюю орбитальную скорость движения планеты, которая совпадает с круговой скоростью:
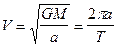 , (I.25)
, (I.25)
где r = a – расстояние от Солнца;
Т – период обращения планеты вокруг светила.
В качестве примера найдем среднюю орбитальную скорость вращения Земли, положив в формулу (I.25) Т = 365,2564·86400 с = 31,56·106 с, а = 149,6·106 км, получим V = 29,78 км/с.
В табл. I.2 приведены параметры всех известных на сегодня спутников планет. Обращаем внимание на наиболее крупные из них. Луна – спутник Земли, Ио, Европа, Ганимед и Каллисто – спутники Юпитера, Титан – спутник Сатурна, Тритон – спутник Нептуна. Это самый крупный спутник в Солнечной системе. Диаметр Тритона 6000 км. Три последние планеты имеют также своеобразные кольца, исследование которых с американской межпланетной станции «Вояджер-2» показало, что они состоят из темного материала, частицы которого имеют размеры порядка метра и более. Не исключено, что это каменные обломки разрушившихся небольших спутников или продукты выбросов мощных вулканических взрывов.
Таблица I.2
Орбитальные параметры спутников планет
| Название | Орбитальный радиус, км | Радиус, 103 м | Масса, 1020 кг | Плотность, 103 кг/м3 |
| Спутник Земли | ||||
| Луна | 384,4 | 734,9 (±0,7) | 3,34 | |
| Спутники Марса | ||||
| Фобос | 9,378 | 13,5×10,7×9,6 | 1,26(±0,1)×10-4 | 2,2(±0,5) |
| Деймос | 23,459 | 7,5×6,0×5,5 | 1,8(±0,15)×10-5 | 1,7(±0,5) |
| Спутники Юпитера | ||||
| Метис (Метида) | 127,96 | ?×20×20 | - | - |
| Адрастея | 128,98 | 12,5×10×7,5 | - | - |
| Амальтея | 181,3 | 135×82×75 | - | - |
| Теба (Фива) | 221,9 | ?×55×45 | - | - |
| Ио | 421,6 | 894±2 | 3,57 | |
| Европа | 670,9 | 480±2 | 2,97 | |
| Ганимед | 1482,3±0,5 | 1,94 | ||
| Каллисто | 1076,6±0,5 | 1,86 | ||
| Леда | - | - | ||
| Гималия | - | - | ||
| Лиситея | - | - | ||
| Элара | - | - | ||
| Ананке | - | - | ||
| Карме | - | - | ||
| Пасифае | - | - | ||
| Синопе | - | - | ||
| Спутники Сатурна | ||||
| Атлас (Атлант) | 136,64 | 19×?×14 | - | - |
| Прометей | 139,35 | 70×50×37 | - | - |
| Пандора | 141,70 | 55×43×33 | - | - |
| Эпиметей | 151,422 | 70×58×50 | - | - |
| Янус | 151,472 | - | - | - |
| Мимас | 185,52 | 0,38±0,01 | 1,24 | |
| Энцелад | 238,02 | 0,8±0,3 | 1,24 | |
| Тефия (Тетис) | 294,66 | 7,6±0,9 | 1,26 | |
| Телесто | 294,66 | ?×12×11 | - | - |
| Калипсо | 294,66 | 15×13×8 | - | - |
| Диона | 377,40 | 10,5±0,3 | 1,44 | |
| Елена (Хелен) | 377,40 | 18×?×15 | - | - |
Окончание табл. I.2
| Название | Орбитальный радиус, км | Радиус, 103 м | Масса, 1020 кг | Плотность, 103 кг/м3 |
| Рея | 527,04 | 24,9±1,5 | 1,33 | |
| Титан | 1221,85 | 1345,7±0,3 | 1,881 | |
| Гиперион | 1481,1 | 175×120×100 | - | - |
| Япет | 3561,3 | 18,8±1,2 | 1,21 | |
| Феба | 115×110×105 | - | - | |
| Спутники Урана | ||||
| Корделия | 49,75 | ~25 | - | - |
| Афелия | 53,77 | ~25 | - | - |
| Бианка | 59,16 | ~25 | - | - |
| Крессида | 61,77 | ~30 | - | - |
| Дездемона | 62,65 | ~30 | - | - |
| Джульетта | 64,63 | ~40 | - | - |
| Порция | 66,10 | ~40 | - | - |
| Розалинда | 69,93 | ~30 | - | - |
| Беллинда | 75,25 | ~30 | - | - |
| Пак | 86,00 | - | - | |
| Миранда | 129,8 | 0,71 | 1,26±0,39 | |
| Ариэль | 191,2 | 14,4 | 1,65±0,30 | |
| Умбриэль | 266,0 | 11,8 | 1,44±0,28 | |
| Титания | 435,8 | 34,3 | 1,59±0,09 | |
| Обертон | 582,6 | 28,7 | 1,50±0,10 | |
| Спутники Нептуна | ||||
| Тритон | 354,3 | 1300±250 | (5) | |
| Нереида | ~200 | - | - | |
| Спутник Плутона | ||||
| Харон | 19,1 | ~500 | - | (0,8) |
Примечание: В скобках – неточные данные, знак вопроса – нет данных.
Солнце. Основные характеристики
Солнце относится к классу небольших звезд, достаточно далеко проэволюционировавших в своем развитии. Возникло оно около 5 млрд. лет назад и в настоящее время имеет массу ~2,1033 г, радиус – 696000 км, среднюю плотность вещества – 1,41 г/см3, ускорение силы тяжести на поверхности – 274 м/с2.
Видимый бело-желтый диск Солнца – это его фотосфера, представляющая горячую плазменную атмосферу звезды с температурой поверхности 6000 К (напомним, что К – термодинамическая температура Кельвина. Нормальная температура 0°С = 273 К. Величина ‑273,16°С называется абсолютным нулем температуры).
В Солнце сосредоточено более 99%всей массы Солнечной системы. Угловая скорость вращения Солнца, наблюдаемая по фотосфере, убывает по мере удаления от экватора. Период вращения на экваторе равен 25 суткам, вблизи полюсов – 30 суткам. Линейная скорость вращения на экваторе близка 2 км/с, т. е. много медленнее скорости вращения Земли и других планет, но происходит в том же направлении. Все это подтверждает предположение, что мы наблюдаем вращение плазменной атмосферы и что внутреннее твердое тело звезды может вращаться с иной скоростью. Напомним, что плазмой называется газ, значительная часть атомов которого находится в ионизированном состоянии.
Солнце является мощным источником тепловой, электромагнитной и гравитационной энергии. Эта энергия равномерно рассеивается в космическое пространство и на долю Земли и планет приходится лишь малая ее часть.
В оптическом диапазоне спектра Земля, например, получает 1,96 кал/см2·мин, или 1,37·103 Вт/м2. Эта величина называется солнечной постоянной. Она меняется в зависимости от гелиоцентрического расстояния и сильно меняется от планеты к планете.
Полная светимость Солнца определяется из выражения:
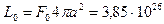 Вт, (I.30)
Вт, (I.30)
где a = 149,6·106 м; 4pа2 – площадь поверхности сферы радиусом в 1 а. е.
Каждый квадратный метр звезды излучает энергии в секунду
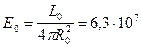 Вт/м2, (I.31)
Вт/м2, (I.31)
т. е. в 10000 раз больше, чем получает вся Земля за одну минуту.
Спектр излучения Солнца лежит в широком диапазоне частот и длин волн (рис. 4) – от радиоизлучения (метровые волны) до гамма-излучения (длина волны l менее 10-12 м). Как видно из рисунка, максимум энергии излучения приходится на оптическую и инфракрасную части спектра. Крайнюю левую часть спектра занимают волны жесткого ультрафиолетового и рентгеновского излучения, крайнюю правую – радиоизлучения.
Рис. 4. Спектр излучения Солнца
Поскольку интенсивность излучения зависит только от изменения температуры с глубиной, то по наблюдениям интенсивности выходящего от звезды излучения можно составить представление об изменении температуры в ее недрах. Максимальная температура Солнца – 6150 К – наблюдается в зеленой части спектра (l = 5000 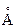 ). Напомним, что 1 Ангстрем = 10-10 м. В красном (l = 6400 – 7600
). Напомним, что 1 Ангстрем = 10-10 м. В красном (l = 6400 – 7600 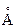 ) и фиолетовом (l = 3900 – 4500
) и фиолетовом (l = 3900 – 4500 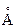 ) частях спектра температура близка 5800 К. В ультрафиолетовом диапазоне (l = 1000
) частях спектра температура близка 5800 К. В ультрафиолетовом диапазоне (l = 1000 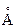 ) температура уменьшается до 4500 К, а в радиодиапазоне на l = 1 м возрастает до 106 К.
) температура уменьшается до 4500 К, а в радиодиапазоне на l = 1 м возрастает до 106 К.
Столь различные температуры не могут исходить только из одной фотосферы, ибо физические условия на ней довольно однородны. В целом на долю светового излучения Солнца приходится 81% энергии, на долю теплового – около 18%, а на долю ультрафиолетового – менее 1%. Чтобы лучше понять природу такого распределения энергии излучения, которое, как мы увидим, играет огромную роль в жизни Земли, рассмотрим основные черты строения внешних оболочек Солнца. Внутреннее строение и энергетику его мы будем изучать в других главах.
Атмосфера Солнца состоит из трех главных уровней – фотосферы, хромосферы и короны (рис. 5). На каждом из этих уровней идут различные физические процессы.
Рис. 5. Внутреннее строение Солнца
Фотосфера представляет собой нижний наиболее активный светопроводящий слой атмосферы. Это граница прозрачности звездного вещества, видимого нами в виде бело-желтого диска Солнца.
На фотографиях поверхность фотосферы покрыта гранулами. Это неустойчивые образования размером от 700 до 1400 км, которые непрерывно появляются и распадаются, создавая впечатление кипящей поверхности. Фотосфера излучает энергию в оптическом и инфракрасном диапазонах. Потери энергии непрерывно пополняются притоком ее из более глубоких слоев. Этот процесс поддерживает стационарность излучения и осуществляется за счет процессов поглощения и переизлучения. Перенос энергии происходит также конвективным путем с помощью гранул, представляющих собой своеобразные конвективные ячейки. Горячее вещество выносится из недр на поверхность, где оно охлаждается и вновь погружается. В промежутках между гранулами наблюдается выброс вещества – спикулы и факелы. Толщина фотосферы около 500 км.
Следующий слой солнечной атмосферы – хромосфера – простирается на расстоянии 15000 – 20000 км и имеет ярко-красный цвет. Она наблюдается при солнечном затмении в виде алого кольца вокруг черного диска Солнца. Температура хромосферы порядка 20000 К.
В хромосфере хорошо видны выбросы горячей плазмы – спикулы (протуберанцы). Высота выбросов достигает 12 тыс. км, а поперечные размеры – 1000 км.
Над хромосферой располагается корона, размеры которой колеблются в зависимости от активности Солнца. Внутренняя корона простирается на 300 – 500 тыс. км и имеет колоссальную температуру – в 1 млн. градусов Кельвина. Она состоит из ионизированных светящихся газов. Внешняя корона представляет собой туманное свечение солнечного света на пылевых частицах, концентрирующихся вокруг Солнца на расстоянии до 80 млн. км. Поэтому эта часть короны имеет светло-желтый оттенок. По мере удаления от хромосферы температура короны понижается, на орбите Земли составляет 200000 К. Периферия короны состоит из разреженных электронных облаков, выбрасываемых Солнцем, которые, будучи вмороженными в его магнитное поле, движутся с большими скоростями, достигающими 30 км/с.
| Рис. 6. Магнитное поле Солнца |
Следует сказать, что в результате осевого вращения Солнце продуцирует мощное магнитное поле, силовые линии которого «приклеиваются» к высокопроводящей плазме короны и вытягиваются в виде спирали далеко в межпланетное пространство (рис. 6). В ходе солнечной активности структура секторного магнитного поля может менять свою форму и даже число секторов.
Возвращаясь к энергетике солнечного излучения, мы теперь можем сказать, что основная доля оптического и инфракрасного излучения исходит из фотосферы, имеющей температуру около 5800 К. Низкотемпературное излучение – 4500 К – соответствует нижним слоям хромосферы. Радиоизлучение и рентгеновское излучение исходят из короны, имеющей в нижней своей части температуру 106 К. Хромосфера и корона прозрачны для оптического и инфракрасного излучения фотосферы. Что же в таком случае питает их энергией и создает столь высокую температуру?
Мы видели, что в фотосфере наряду с лучистым переносом энергии происходит и конвективное перемешивание вещества, фиксируемое в виде многочисленных гранул и спикул, а также мощных протуберанцевых выбросов плазмы. Это механическое движение огромных масс вещества на поверхности гигантской звезды должно приводить к мощным акустическим колебаниям окружающей атмосферы (вспомните шум кипящей воды в чайнике). Иными словами, поверхность звезды буквально сотрясается от оглушительного рева, звук которого со сверхзвуковыми скоростями распространяется через хромосферу во все стороны от Солнца. Однако по мере распространения в солнечную корону, где плотность вещества быстро убывает, обычные звуковые волны превращаются в ударные. Как известно из физики плазмы, в ударных волнах энергия механического движения быстро переходит в тепловую. Поэтому небольшая по массе и сильно разреженная корона нагревается до столь высоких температур.
Другой важной характеристикой Солнца является его периодическая активность, проявляющаяся в появлении на фотосфере темных пятен, в хромосфере и короне – вспышек, факелов, протуберанцев. Установлена 11-летняя периодичность явления солнечной активности. Наиболее ярким показателем солнечной активности является изменение числа темных пятен и их размеров на диске Солнца. Температура их на 1500 К ниже температуры окружающей фотосферы, диаметр достигает 2 – 50 тыс. км. В рельефе поверхности пятна фиксируются в виде впадин глубиной 700 – 1000 км. Важной характеристикой пятна является его магнитное поле, напряженность которого достигает гигантской величины – 4·105 А/м. Для сравнения укажем, что напряженность магнитного поля Земли в районе полюсов всего 70 А/м.
Время жизни пятен – от нескольких часов до нескольких месяцев. Обычно уровень солнечной активности характеризуется числом Вольфа
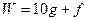 , (I.32)
, (I.32)
где g – число групп пятен; f – общее число всех пятен, видимых на диске Солнца.
Солнечная активность оказывает большое влияние на климат, погоду, жизнь биосферы Земли. Причины солнечной активности до сих пор являются предметом дискуссий. Есть по крайней мере две группы гипотез – эндогенные, объясняющие периодичность активности внутризвездными процессами, и экзогенные, связывающие ее с приливным взаимодействием с планетой-гигантом Юпитером.
С эндогенными гипотезами пока еще много неясного, хотя успехи изучения физики звезд, как мы увидим, весьма впечатляющи.
Экзогенные причины цикличности солнечной активности привлекают внимание сходством периодов обращения Юпитера вокруг Солнца (11,86 года) и средней длительностью солнечного цикла (11,13 года). Обнаруживается связь между изменением гелиоцентрического расстояния Юпитера с числом пятен на Солнце. Величина юпитерианского прилива на Солнце составляет всего 1 мм. Однако исследования показали, что здесь важно не изменение скорости приливного смещения центра Солнца (первая производная), а толчок (третья производная). Вклад планет в толчок возрастает на порядок величин.
Дата добавления: 2015-06-27; просмотров: 1632;
