Физическое состояние вещества геосфер
Плотность. Средняя плотность самой верхней литосферной оболочки Земли толщиной 0 – 33 км известна из непосредственных определений и ряда вполне приемлемых экстраполяций – она составляет 2,7 – 3,0 г/см3.
Средняя плотность вещества Земли легко определяется из закона тяготения Ньютона:
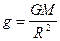 . (II.1)
. (II.1)
Здесь G = 6,67·10-8 см3/г·с2 (в системе СГС) – гравитационная постоянная; М – масса однородной шарообразной Земли радиусом R. Отсюда можно найти массу Земли, если известна средняя плотность заполняющего ее вещества:
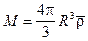 , (II.2)
, (II.2)
откуда с учетом (II.1) находим
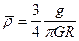 . (II.3)
. (II.3)
Подставляя в правую часть выражения (II.1) средние значения g =
= 982,0 см/с2 и R = 6,371·108 см, получаем:
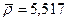 г/см3. (II.4)
г/см3. (II.4)
Таким образом, простой расчет показывает, что средняя плотность Земного шара почти в два раза больше средней плотности литосферной оболочки Земли. Следовательно, дефицит плотности должен восполняться на более глубоких уровнях планеты.
Характер изменения плотности с глубиной должен при этом удовлетворять закону изменения скоростей упругих волн, а распределение масс – наблюдаемому моменту инерции вращающейся Земли:
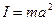 . (II.5)
. (II.5)
Кроме того, плотность на поверхности Земли должна быть равна фактической средней плотности литосферы. Поэтому принятие наиболее простого закона непрерывно-монотонного возрастания плотности с глубиной в соответствии с гидростатической моделью хотя и дает плотность в центре Земли порядка 10 – 11 г/см3, близкую к вероятной (Магницкий, 1965), однако не отвечает ни одному из вышеперечисленных условий.
Близкое к реальному изменение плотности с глубиной было определено с учетом данных сейсмологии, среднего для Земли значения момента инерции I, известного по спутниковым данным, и средней плотности 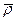 . Например, в случае однородной модели момент инерции был бы равен:
. Например, в случае однородной модели момент инерции был бы равен:
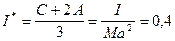 . (II.6)
. (II.6)
Здесь С – момент инерции относительно полярной оси; А – момент инерции относительно экваториальной оси. Согласно наблюдениям значение I* для реальной Земли оказалось равно (Мельхиор, 1976):
I/Ma2 = 0,33089.
Это соответствует значительной концентрации массы в центре планеты. В этой связи интересно сравнить I* для Луны – он равен
0,402 ± 0,02, т.е. Луну с хорошим приближением можно рассматривать как однородное тело.
В последние годы стало ясно, что учета только I* оказывается недостаточно для того, чтобы объяснить особенности и периоды колебания земного шара, возникающие под действием сильных землетрясений (типа чилийского, 1961 г.) и суточных приливообразующих сил. Дело в том, что в случае полностью твердой Земли частота ее колебания под действием приложенной силы будет несколько выше, чем частота колебаний шара с «жидким» ядром. «Болтание» твердого субъядра относительно покрывающей его жидкой оболочки внешнего ядра увеличивает период колебания всей системы. Это и было обнаружено при исследовании периодов колебания Земли М. Молоденским (1961) и Г. Джеффрисом (1960).
С учетом этих данных и на основе ранее рассчитанной модели внутреннего строения Земли (Гутенберг, 1963; Мельхиор, 1976) методом машинного перебора установили, что для удовлетворения I* =
= 0,33089 и для получения наилучшего согласия с крутильными и сфероидными колебаниями низких порядков (при прочих вышеперечисленных условиях) необходимо ввести аномальный скачок плотности на границе с ядром, т.е. на глубине 2900 км. Близкие результаты были получены Ф. Прессом (1968), рассмотревшим пять миллионов моделей внутреннего строения Земли, соответствующих данному распределению скоростей. Путем согласования значений массы Земли, ее момента инерции, времени пробега P- и S-волн и собственных колебаний на низших гармониках было выбрано четыре модели, удовлетворяющие всем условиям (табл. II.2). В частности, согласно данным Б. Болта и К. Буллена, в ядре имеются два скачка плотности на расстояния 1210 и 1660 км от центра Земли при общем радиусе ядра 3470 км (табл. II.2).
Таблица II.2
Строение мантии и ядра Земли (по Мельхиору, 1975)
| Зона | R, км | Скорость, км/с | Плотность, г/см3 |
| Мантия | 10,0 | 8,33 | |
| Внешнее ядро | 10,03 | 9,6 | |
| 10,31 | 10,05 | ||
| Внутреннее ядро | 11,5 | ||
| 11,23 | 13,23 |
Давление и сила тяжести внутри Земли. Нарастание давления Р с глубиной r в недрах Земли подчиняется гидростатическому закону:
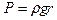 , (II.7)
, (II.7)
т.е. уплотнение пропорционально весу вещества слоя, приходящегося на единицу площади. Таким образом, давление изменяется как непрерывная функция, возрастающая с глубиной от 0 атм на поверхности до 1,3×106 атм на границе внешнего ядра и 4×106 атм в центре Земли (Магницкий, 1965; Гутенберг, 1963) (рис. 10).
Зная закон распределения плотности с глубиной, можно рассчитать изменение ускорения силы тяжести:
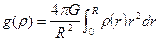 , (II.8)
, (II.8)
где R – расстояние от центра Земли до измеряемого уровня на шаре. Ускорение силы тяжести медленно возрастает до границы внешнего ядра с 980 до 998 см/с2, на границе испытывает резкий скачок до 10,37 см/с2 и затем быстро уменьшается к центру Земли, где оно равно нулю (рис. 10). Столь резкое уменьшение гравитации в твердом ядре, несомненно, должно иметь большое значение для создания здесь определенных условий дифференциации протовещества планеты. В самом деле, если ускорение силы тяжести на границе внешнего ядра по сравнению с поверхностью Земли увеличивается почти на 2,7 см/с2, то центробежное ускорение уменьшается примерно на половину (порядка 1,6 см/с2). Со стороны центра Земли вектор ускорения силы тяжести будет направлен в сторону внешней границы «жидкого» ядра с одновременным увеличением в том же направлении центробежного ускорения. Из этого следует, что при такой структуре поля силы тяжести дифференциация вещества будет иметь большую составляющую по направлению от центра Земли. Следовательно, в сторону субъядра могут быть отмобилизованы лишь наиболее тяжелые компоненты протовещества, причем для их перемещения потребуется дополнительная сила, направленная не вдоль радиуса. Такой силой может быть конвективное движение.
| Рис. 10. Изменение с глубиной давления P (Па), плотности s (г/см3), объемного модуля k, модуля жесткости m (Па) и ускорения силы тяжести g (м/с2) для модели Буллена; Р, k, m выражены в ед. ×1011 дин×см-2 |
Рассмотренные данные суммированы в табл. II.3 (Буллен, Хаддон, 1967):
Таблица II.3
Дата добавления: 2015-06-27; просмотров: 898;
