Форма и размеры Земли
Физическая поверхность Земли представляет собой сочетание бесконечно большого числа неровностей. Она состоит из океанов, морей и материков с островами. Поверхность океанов в их спокойном состоянии ровная, а суша, составляющая только 29 % от общей площади Земли, представляет собой сложные сочетания гор, возвышенностей, равнин и низменностей. Поэтому поверхность Земли не имеет математического выражения, хотя для решения задач науки и практики требуется знать пространственное положение ее точек. Устанавливать их удобно относительно вспомогательной поверхности, близкой к реальной (физической) поверхности Земли. Такую поверхность называют поверхностью относимости, за которую принимается основная уровенная поверхность Земли, в каждой точке которой нормаль совпадает с направлением отвесной линии (с направлением силы тяжести). Это поверхность воды океанов и открытых морей, находящаяся в спокойном состоянии и мысленно продолженная под материками так, что к ней отвесные линии перпендикулярны во всех точках на Земле. Выбор поверхности воды океанов и морей за уровенную поверхность Земли, объясняется тем, что поверхность открытых водных пространств занимает 71 % общей площади Земли.
В 1873 г. немецкий физик И. Б. Листинг назвал эту поверхность поверхностью геоида. Однако и фигура геоида сложна и строго неопределима, поскольку зависит от малоизученного распределения масс внутри Земли. Поэтому поверхность геоида не соответствует поверхности ни одной правильной математической фигуры, что не позволяет проводить расчеты, связанные с обработкой геодезических измерений на земной поверхности.
По предложению ученого М. С. Молоденского вместо геоида в качестве промежуточной поверхности относимости используется квазигеоид, выполняющий роль «уровня моря». Положение его поверхности рассчитывается на основе гравиметрических измерений (см. 2.2). Поверхности квазигеоида и геоида совпадают с поверхностью Мирового океана и различаются по высоте на суше не более чем на 2,5 м.
Геоид и квазигеоид по форме близко подходят к правильной математической фигуре – эллипсоиду вращения. Поэтому в качестве основной уровенной поверхности при обработке геодезических измерений, выполняемых на земной поверхности принята поверхность эллипсоида вращения, представляющего собой фигуру, полученную в результате вращения эллипса вокруг его малой оси (земной) эллипсоид.
Угол между отвесной линией pq к поверхности геоида в данной точке и нормалью mn к поверхности эллипсоида называется уклонением отвесной линии e (рис. 2.1). В среднем, значение e составляет 3–4″, а в местах аномалий достигает десятков секунд.
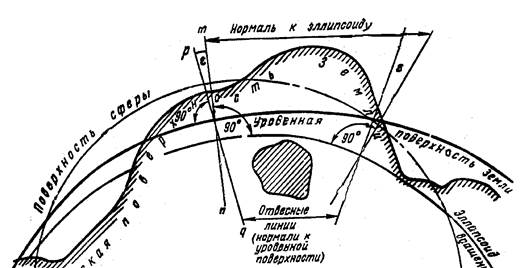
Рис. 2.1
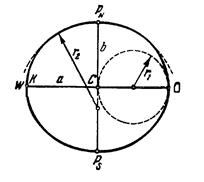
Земной эллипсоид характеризуется следующими основными элементами (рис. 2.2.): малой полуосью (полярный радиус) 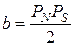 , которая совпадает с осью вращения Земли; большой полуосью (экваториальный радиус)
, которая совпадает с осью вращения Земли; большой полуосью (экваториальный радиус) 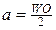 , которая перпендикулярна оси вращения Земли и полярным сжатием
, которая перпендикулярна оси вращения Земли и полярным сжатием 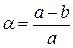 .
.
 Элементы земного эллипсоида, рассчитан–ные Деламбром (1800), Бесселем (1841), Хейфордом (1909) и другими учеными неоди–наковы, так как вычислены по геодезическим измерениям разных по протяженности дуг ме–ридианов и параллелей.
Элементы земного эллипсоида, рассчитан–ные Деламбром (1800), Бесселем (1841), Хейфордом (1909) и другими учеными неоди–наковы, так как вычислены по геодезическим измерениям разных по протяженности дуг ме–ридианов и параллелей.
 Земной эллипсоид, принятый для обработки геодезических измерений и установления единой государственной системы координат называется референц-эллипсоидом.
Земной эллипсоид, принятый для обработки геодезических измерений и установления единой государственной системы координат называется референц-эллипсоидом.
На территории СССР пользовались эллипсоидом Ф. В. Бесселя до 1946 г. Однако этот эллипсоид был рассчитан в основном по данным Западной Европы. На Дальнем Востоке его поверхность сильно уклонялась от поверхности Земли.
Более точные результаты размеров земного эллипсоида были получены в 1940 г.Ф. Н. Красовским и А. А. Изотовым по результатам астрономо-геодезических работ, выполненных на территории СССР, Западной Европы и США. Размеры земного эллипсоида, получившего название «референц-эллипсоида Красовского», были приняты для геодезических и картографических работ на всей территории СССР. Отклонения поверхности референц-эллипсоида Красовского от поверхности геоида не превышают 150 м. Точкой ориентирования референц-эллипсоида Красовского является центр круглого зала Пулковской обсерватории, широта В0 и долгота L0 которого определены из астрономических наблюдений и приняты исходными, а поверхность эллипсоида совмещена со средним уровнем воды в Финском заливе и отмечена на Кронштадском футштоке.
В настоящее время основные геометрические параметры общеземного эллипсоида определяются более точными методами с использованием искусственных спутников Земли. Для сравнения в табл. 2.1 приведены размеры земного эллипсоида, определенные Бесселем, Красовским и в глобальной геоцентрической системе координат WGS – 84 (World Geodetic System 1984).
Таблица 2.1.
Размеры земного эллипсоида
| Автор | Годы | Размеры земного эллипсоида | ||
| а, м | b, м | a | ||
| Бессель | 6 377 397 | 6 356 079 | 1:299,15 | |
| Красовский | 6 378 245 | 6 356 863 | 1:298,3 | |
| WGS - 84 | 6 378 137 | 6 356 752 | 1: 298,257 |
При картографических работах (составление карт мелких масштабов) Землю достаточно принимать за шар, объем которого равен объему земного сфероида. Исходя из размеров эллипсоида Красовского R = 6 371 110 м.
Дата добавления: 2015-06-27; просмотров: 884;
