Нормальное и аномальное гравитационное поле

Как и во всех геофизических полях, в гравитационном поле Земли можно выделить нормальное и аномальное поле.

Нормальным полем считается теоретически рассчитанное поле для поверхности эллипсоида вращения или сфероида, которым в первом приближении является Земля. Величина сжатия земного эллипсоида равна:

α = (a – b) / a ≈ 1 / 300

где а и b - большая и малая оси эллипсоида (а – b = 21,38 км)

Задача о распределении силы тяжести на поверхности сфероида была решена французским математиком Клеро в 1743 году. Исходя из допущения, что Земля состоит из однородных жидких слоев, плотность которых увеличивается к ее центру, он вывел формулу для вычисления величины нормальной силы тяжести g_o в зависимости от географической широты φ пункта Земли. В упрощенном виде она выглядит следующим образом:

g_o = g_Э (1 + β sin² φ),

где g_Э - значение силы тяжести на экваторе; β – числовой коэффициент, определяющийся соотношением центробежной силы и силы тяжести на экваторе.

Путем многочисленных измерений силы тяжести на поверхности Земли и на основе теоретических разработок о распределении плотности внутри нее, были получены значения числового коэффициента для этой формулы. Практически, из-за того, что разные авторы использовали различные исходные данные и предпосылки, существует несколько формул определения g_o.

В действительности Земля имеет более сложную форму и более сложное внутреннее строение. Поэтому наблюдаемое на реальной поверхности гравитационное поле будет отличаться от нормального поля. Как известно, разность между наблюденным полем и нормальным составляет аномальную часть. В общем виде аномальное поле можно представить как:

∆g = g_н – g_o

где g_н - наблюденное поле силы тяжести.

Однако помимо внутреннего строения земной коры в наблюденное поле силы тяжести входит влияние некоторых приповерхностных факторов. Чтобы их исключить вводят ряд поправок (редукций) - за высоту пункта наблюдений над уровнем моря; за влияние промежуточного слоя пород, заключенного между уровнем моря и дневной поверхностью; за влияние окружающих точку наблюдения масс рельефа.

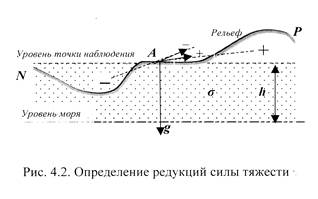
Поправка за высоту вводится для приведения силы тяжести к уровню моря. Для ее вычисления полагают, что между точкой наблюдения А (рис. 4.2), расположенной на некоторой высоте h, и уровнем моря нет притягивающих масс.

Эта поправка учитывает убывание силы тяжести с высотой (примерно на 0,3 мГл / м) при условии, что между поверхностью наблюдения и поверхностью приведения (уровнем моря) нет никаких масс. Поэтому ее называют поправкой за свободный воздух.

Поправка за промежуточный слой учитывает влияние масс, расположенных между точкой наблюдения А и уровнем моря (см. рис 4.2). Формула для вычисления этой поправки выведена в предположении, что Земля имеет ровный рельеф, и слой между поверхностью наблюдения и уровнем моря можно представить в виде плоско-параллельного безграничного слоя, однородного по составу.

Поправка имеет отрицательный знак, потому что притяжение промежуточного слоя, находящегося под пунктом наблюдений, увеличивает силу тяжести.

Поправка за влияние окружающего рельефа местности (или топографическая поправка) вводится в связис тем, что при определении поправки за промежуточный слой поверхность Земли предполагалась ровной. В реальности влияние рельефа может достигать нескольких десятков миллиГал.

Избыток или недостаток масс, связанный с формами рельефа, всегда уменьшает наблюденное значение силы тяжести. Поэтому эта поправка всегда имеет положительный знак.

В самом деле, избыток масс над уровенной поверхностью, проходящей через точку наблюдения А, под отрезком АР рельефа Земли (см. рис. 4.2) создает добавочную силу (+), направленную в сторону центра избытка масс (+), и вертикальная составляющая этой силы направлена вверх, то есть уменьшает значение g. Недостаток масс под уровенной поверхностью над отрезком рельефа АN создает добавочную силу (-), направленную в сторону центра недостатка масс (-), вертикальная составляющая которой направлена вверх и тоже уменьшает величину g относительно той величины, которая должна была быть при однородном распределении масс под уровенной поверхностью.

Введение всех указанных поправок позволяет привести аномальное поле силы тяжести к некоторой поверхности, которую назвали геоидом (что означает «землеобразный»). Под геоидом подразумевают поверхность, совпадающую на океанах с уровнем воды и мысленно продолженную под континенты.

Теперь, мы имеем возможность дать более точное определение аномалии силы тяжести.

Аномалией силы тяжести называется разность между наблюденным значением силы тяжести на дневной поверхности с поправками и нормальным значением, вычисленным по соответствующей формуле.

Таким образом, выражение для аномалии силы тяжести может быть записано:

∆g =g_н– g₀+ ∆´g