Расширение потока в косом срезе сопла 1 страница
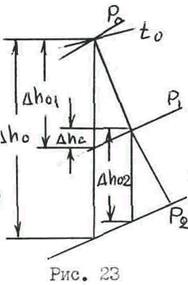
Сопла обычно бывают наклонены под углом a1п к направлению вращения рабочих лопаток. Вследствие этого концевая часть сопла от расчетного выходного сечения 1-1' (рис. 13) до действительного выходного сечения 1-2 представляет собой так называемый косой срез, который поток должен пройти до входа на рабочие лопатки.
Косой срез начинает работать, если давление за сопловой решеткой Р1 ниже критического значения Ркр. В этом случае весь процесс складывается как бы из двух этапов. На первом этапе происходит расширение в собственно сопловом канале, ограниченном четырьмя стенками (до расчетного выходного сечения 1-1’). Здесь давление падает от величины Р0 до Ркр, а остальной перепад Ркр – Р1 срабатывается в косом срезе.
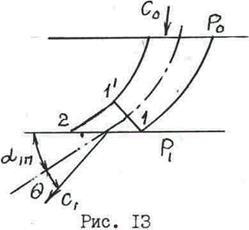 При этом скорость потока становится сверхзвуковой, а увеличение удельного объема пара (газа) приводит к отклонению потока в косом срезе от осевой линии в сторону открытой части на угол q.
При этом скорость потока становится сверхзвуковой, а увеличение удельного объема пара (газа) приводит к отклонению потока в косом срезе от осевой линии в сторону открытой части на угол q.
Именно эта величина и представляет интерес для дальнейших расчетов. Угол отклонения потока за счет расширения в косом срезе q может быть найден из выражения
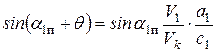
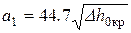 – критическая скорость в сечении 1-1’,
– критическая скорость в сечении 1-1’,
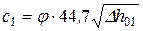 – скорость потока на выходе из косого среза,
– скорость потока на выходе из косого среза,
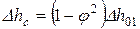 – потеря энергии в сопловом канале,
– потеря энергии в сопловом канале,
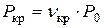 – критическое давление.
– критическое давление.
В реальных условиях работы сопловой решетки угол q не должен быть больше 3 ¸ 5°.
Расчет сопловых решеток
Цель расчета – определить геометрические размеры сопловой решетки для конкретной турбинной ступени. Это – часть теплового расчета турбины.
Исходные данные:
G – кг/сек – массовый расход рабочего вещества через решетку,
Р0 – МПа (кгс/см2), давление перед решеткой,
t0 – °С – температура перед решеткой,
Р1, – МПа (кгс/см2) – давление за решеткой,
Dср – м – средний диаметр облопатывания,
a1п – геометрический угол выходной кромки профиля; принимается в пределах 11¸ 24 °.
Определяется отношение давлений на решетке и выбирается тип сопловой решетки:
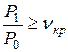 – решетка со сходящимися сопловыми каналами,
– решетка со сходящимися сопловыми каналами,
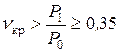 – решетка со сходящимися сопловыми каналами с расширением в косом срезе,
– решетка со сходящимися сопловыми каналами с расширением в косом срезе,
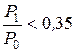 – решетка с расходящимися сопловыми каналами.
– решетка с расходящимися сопловыми каналами.
Расчет сопловой решетки со сходящимися сопловыми каналами без расширения в косом срезе
По исходным параметрам начинается построение процесса расширения в тепловой диаграмме (рис. 15) и определяется располагаемый теплоперепад Dh01, а затем теоретическая скорость истечения 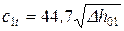 м/с
м/с
Дальнейший расчет производится в двух приближениях.
Расчет в первом приближении
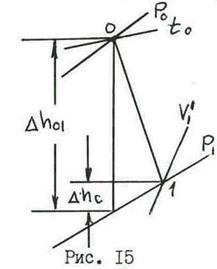 Ориентировочно оценивается коэффициент потери скорости j1 = 0,96 ¸ 0,98, а за тем находится действительная скорость истечения c’1 и потеря энергии на решетке Dh’c.
Ориентировочно оценивается коэффициент потери скорости j1 = 0,96 ¸ 0,98, а за тем находится действительная скорость истечения c’1 и потеря энергии на решетке Dh’c.
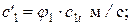
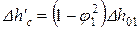
Далее строится действительный процесс 0-1 и в точке 1 снимается удельный объем пара на выходе из решетки \/'1 м3/кг.
Определяется скорость звука при параметрах выходного сечения 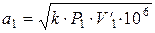 м/с и число Маха
м/с и число Маха 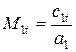
В зависимости от принятого угла a1п и получившегося числа М1t по атласу профилей подбирается подходящий профиль.
Например, С-9015А или С-9018Б.
С – профиль предназначен для сопловых решеток
А – дозвуковая решетка, М £ 0,9
Б – околозвуковая решетка, М = 0,9 ¸ 1,2
Первые две цифры соответствуют углу a0п, вторые – a1п.
Для подобранного профиля из атласа берется рекомендуемый относительный шаг 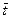 и угол установки aу. Далее по графику в зависимости от
и угол установки aу. Далее по графику в зависимости от 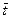 и aу находится a1эф. График имеет вид, представленный на рис. 16.
и aу находится a1эф. График имеет вид, представленный на рис. 16.
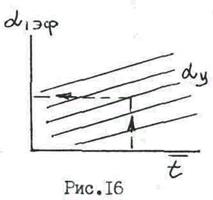 Далее определяется высота выходных кромок сопловой решетки
Далее определяется высота выходных кромок сопловой решетки
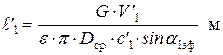
В данной формулеe – степень парциальности впуска – отношение длины дуги, занятой сопловой решеткой, к длине всей окружности ступени на среднем диаметре облопатывания. Первоначально принимается e = 1 и делается расчет. Если  < 0,012 м, то делается пересчет: т.е., принимается желательная величина
< 0,012 м, то делается пересчет: т.е., принимается желательная величина 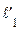 >
>  и пересчитывается e, которая будет меньше единицы. Из атласа находится хорда профиля b1, определяется шаг решетки t1 =
и пересчитывается e, которая будет меньше единицы. Из атласа находится хорда профиля b1, определяется шаг решетки t1 =  ×b1 и отношение
×b1 и отношение 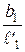 .
.
Расчет во втором приближении
По графикам определяются  и
и
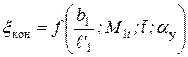
Графики имеют вид, представленный на рис. 17 и 18.

Определяются 
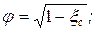

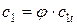 .
.
Повторно строится процесс в тепловой диаграмме с учетом нового значения Dhc, снимается величина удельного объема и находится высота выходных кромок решетки во втором приближении
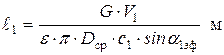
Число сопловых каналов 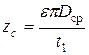 .
.
Полученная цифра округляется до ближайшего целого значения; если при этом e < 1 то пересчитывается e. Если же e = 1, то после округления zc – пересчет t1. Все остальное – без изменений.
Расчет сопловой решетки со сходящимися сопловыми каналами с расширением в косом срезе
 При наличии расширения в косом срезе в минимальном сечении скорость течения будет равна скорости звука, а давление – критическому. Определяется критическое давление
При наличии расширения в косом срезе в минимальном сечении скорость течения будет равна скорости звука, а давление – критическому. Определяется критическое давление 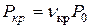 .
.
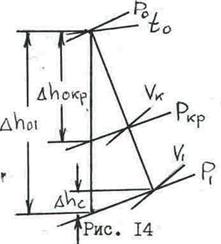
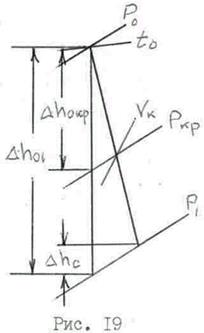
По исходным данным строится теоретический процесс в тепловой диаграмме (рис. 19), откуда снимаются полный располагаемый теплоперепад Dh01 и теплоперепад, соответствующий критическому перепаду давлений Dh0кр.
Определяется полная теоретическая скорость истечения 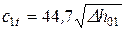 . Принимается коэффициент j и оценивается потеря энергии в соплах Dhc. По результатам построения определяется удельный объем в минимальном сечении \/км3/кг и критическая скорость
. Принимается коэффициент j и оценивается потеря энергии в соплах Dhc. По результатам построения определяется удельный объем в минимальном сечении \/км3/кг и критическая скорость 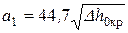 . Оценивается число Маха
. Оценивается число Маха 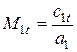 .
.
В зависимости от принятого a1п по атласу подбирается профиль из группы Б, находится 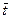 и aу , а затем по графику
и aу , а затем по графику  и подсчитывается высота выходных кромок:
и подсчитывается высота выходных кромок:
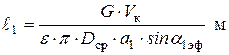
Если 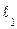 < 0,012 м, то производится пересчет e по аналогии с предыдущим вариантом.
< 0,012 м, то производится пересчет e по аналогии с предыдущим вариантом.
Определяется шаг сопловой решетки t1 и число сопловых каналов. Расчет во втором приближении, как правило, не производится из-за очень небольшой разницы в результатах.
Преобразование энергии на рабочих лопатках
Выходящий из сопел пар (газ) попадает в каналы, образованные рабочими лопатками, и здесь происходит второе преобразование: кинетическая энергия потока превращается в механическую работу вращения рабочего колеса. При обтекании потоком профилей рабочих лопаток на каждой из них возникает подъемная сила, приводящая в движение рабочее колесо турбины. Силу Рz, действующую на каждой лопатке, можно разложить на две составляющие: Рuz – окружную и Рaz – осевую (рис. 20)
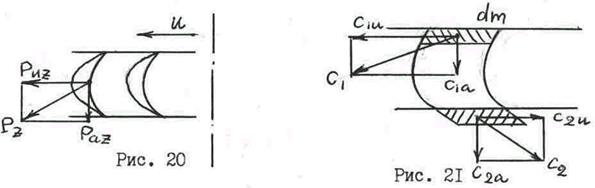
Величина работы, развиваемой колесом, будет определяться только окружными составляющими Рu (окружной силой).
Как полная сила Рz, действующая на лопатку, таки её составляющие, могут быть легко найдены, если применить к каналу, ограниченному двумя соседними рабочими лопатками, известный из механики закон количества движения. Примем следующие обозначения:
G – кг/с – массовый расход рабочего вещества через решетку,
z – количество каналов, через которые этот поток движется,
c1 – м/с – абсолютная скорость потока при входе в канал,
c2 – м/с – то же, при выходе из канала,
dt – сек – произвольный промежуток времени.
Тогда элементарная масса, входящая в канал и выходящая из него за этот промежуток времени
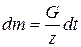 (рис. 21)
(рис. 21)
По закону количества движения 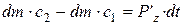 т.е., изменение количества движения за какой-то промежуток времени равно импульсу силы за тот же промежуток времени.
т.е., изменение количества движения за какой-то промежуток времени равно импульсу силы за тот же промежуток времени.
Здесь Р’z – сила, с которой стенки канала действуют на поток, заставляя его изменять направление движения.
Согласно закона Ньютона сила, с которой поток будет действовать на стенки канала, Pz, равна P’z, но противоположна по знаку, т.е., Р’z = – Рz. В результате можно записать
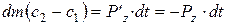
или
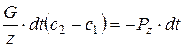
После преобразований 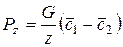 .
.
По аналогии 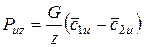 и
и 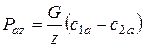 .
.
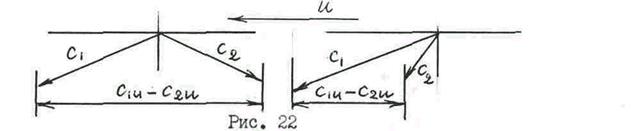
При этом следует помнить, что в скобках находятся проекции векторов скорости и поэтому, подставляя вместо c1u и c2u их значения, следует учитывать не только величину, но и направление этих составляющих скоростей.
Если c1u и c2u направлены в разные стороны (как это чаще всего бывает), то их абсолютные значения следует сложить, и наоборот, если они направлены в одну сторону, вычесть одно из другого (рис. 22).
Для всего рабочего колеса турбины при числе лопаток z окружное усилие определится так:
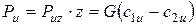 н/кг (м/сек2)
н/кг (м/сек2)
Секундная работа потока (т.е., мощность)
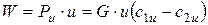 Вт (нм/с или Дж/с)
Вт (нм/с или Дж/с)
Мощность, отнесенная к массе в 1 кг
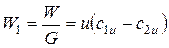 Вт/кг (Дж/(c×кг))
Вт/кг (Дж/(c×кг))
Подобным же образом можно вывести выражение для определения осевой силы
 н
н
Выражения для определения Pu и Рa носят название уравнений Эйлера в честь академика, впервые получившего их в 1754 году.
Степень реакции турбинной ступени
 Степенью реакции турбинной ступени называется отношение располагаемого теплоперепада, приходящегося на рабочую решетку, ко всему теплоперепаду, приходящемуся на ступень
Степенью реакции турбинной ступени называется отношение располагаемого теплоперепада, приходящегося на рабочую решетку, ко всему теплоперепаду, приходящемуся на ступень
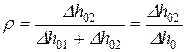

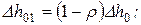

Для ступени активного типа
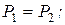
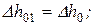
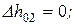

Для ступени с реакцией
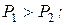
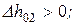
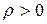
Оптимальная форма профиля рабочих лопаток
Форма профиля, в основном, определяется его геометрическими углами b1п и b2п их соотношением. Исходные уравнения
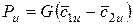 и
и 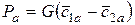
Наивыгоднейший профиль будет такой, у которого возникающая на нем сила Р будет иметь окружное направление, т.е., если Р = Рu,а Ра = 0. При этом Pu имеет наибольшее возможное значение, и совершаемая работа будет максимальной.
Для преобразования исходных уравнений воспользуемся так называемыми "треугольниками скоростей" (рис. 24), которые дают взаимосвязь между абсолютными и относительными скоростями потока и окружной скоростью на входной и выходной кромках профиля. Треугольники скоростей позволяют определить окружные и осевые составляющие каждого вектора скорости.
Примем, что составляющие векторов, направленные по ходу вращения, имеют знак "плюс" (+), а против направления вращения – знак "минус" (-).
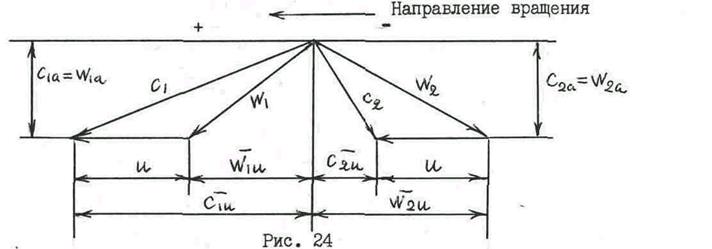
В результате, по треугольникам скоростей получаем:
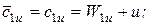
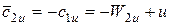
Тогда
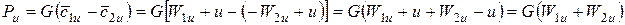
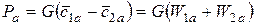
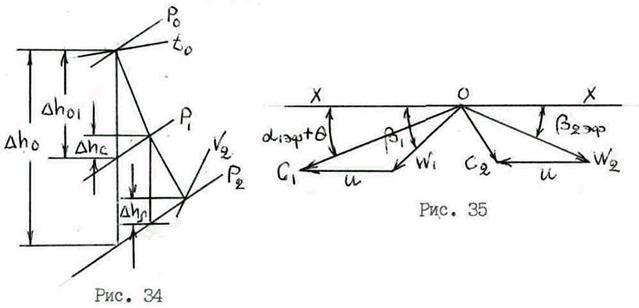
Связь между составляющими векторами относительных скоростей потока на входе и выходе с рабочей решетки дана на рис. 25.
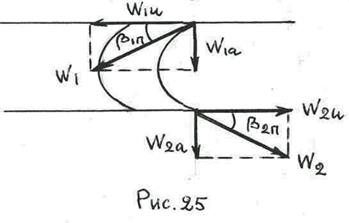
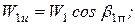

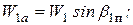
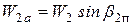
Отсюда
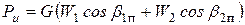

Оптимальный профиль при активном типе облопатывания
В каналах между рабочими лопатками в этом случае давление постоянно и, следовательно, относительная скорость, если не учитывать потери, должна быть постоянной, т.е., 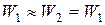 .
.
Тогда 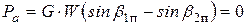
Отсюда следует, что должно быть 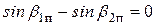 или
или 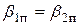 т.е., профиль лопатки должен быть симметричным. В действительности же из-за потерь
т.е., профиль лопатки должен быть симметричным. В действительности же из-за потерь 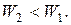
Вследствие этого, как видно из выражения для определения Pu, эта сила будет меньше, чем при отсутствии потерь. Желательно, чтобы сила Pu была по возможности большей. Это может быть в известной степени достигнуто за счет уменьшения угла b2п по сравнению с b1п.
При уменьшении b2п увеличивается cos b, а следовательно и сила Pu. По этим соображениям угол b2п принимается на 3 ¸ 5 ° меньше b1п.
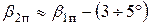
При этом сила Pu при наличии сопротивлений примерно равна силе Pu, при отсутствии сопротивлений, но появляется сила Pa > 0, с чем приходится мириться.
Вывод: в активной турбинной ступени профили рабочих лопаток должны быть близкими к симметричной форме.
Оптимальный профиль при наличии реакции в ступени
При наличии реакции в ступени в межлопаточных каналах происходит дополнительное расширение потока, давление падает, а относительная скорость нарастает. В результате W2 > W1.
Для обеспечения Рa = 0, выражение и стоящее в скобках, должно быть равно 0, т.е.,
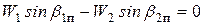
или
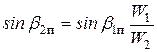
Так как 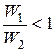 , то sin b1п > sin b2п т.е. b1п > b2п
, то sin b1п > sin b2п т.е. b1п > b2п
Вывод: в турбинной ступени с реакцией профили рабочих лопаток должны быть резко несимметричными.
Потери на рабочих решетках
Коэффициент потери энергии на лопатках xл и скоростной коэффициент y.
Потери на рабочей решетке, так же, как и на сопловой , зависят от большого количества факторов: от формы профиля рабочих лопаток, угла поворота струи на рабочих лопатках, угла установки профиля, шага решетки, хорды профиля и высоты канала, скорости потока и т.д.
Потери на рабочей решетке так же могут быть разделены на две основные группы:
1. Профильные потери
а). трения в пограничном слое,
б). вихревые потери при отрывах потока на профиле,
в). кромочные потери,
г). потери в скачках уплотнения.
2. Концевые потери
а). потери трения в пограничном слое у торцевых стенок,
б). потери вследствие вторичных токов,
в). потери от взаимодействия струи с неподвижным паром (газом) в зазоре между сопловой и рабочей решетками.
Природа потерь на рабочей решетке такова же, что и на сопловой решетке.
Потери трения в пограничном слое зависят в первую очередь от характера пограничного слоя и, соответственно, от числа Маха.

n2 – кинематическая вязкость,
W2 – скорость потока на выходе из канала,
b2 – хорда профиля.
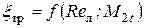 Оптимальное значение числа Рейнольдса Reл = 1,5×105 ¸ 4¸105.
Оптимальное значение числа Рейнольдса Reл = 1,5×105 ¸ 4¸105.
Вихревые потери при отрывах потока на профиле
В отличие от сопловых решеток данная потеря на рабочих лопатках может возникать довольно часто и оказывает значительное влияние на общую величину потерь – как профильных, так и концевых. Отрыву потока на входной кромке профиля предшествует явление удара либо в спинку профиля, либо в его рабочую часть
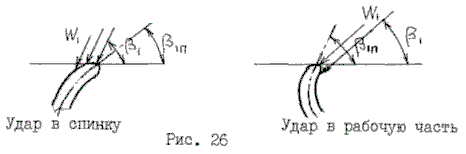
Основной фактор здесь – разность углов b1 – b1п.
Если b1 – b1п> 0, т.е., положительна, то имеет место удар в спинку профиля.
Если же b1 – b1п< 0 – (отрицательна) – удар в рабочую поверхность.
Влияние удара на профильные и концевые потери учитывается отдельными коэффициентами Впр и В’кон, характер которых представляется графиками (рис. 27 и 28).
Кромочные потери
Коэффициент кромочных потерь 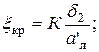 К = 0,1 ¸ 0,3
К = 0,1 ¸ 0,3
а’л – ширина канала в выходном сечении;
d2 – толщина выходной кромки.

Потери в скачках уплотнения
Оцениваются коэффициентом xволн
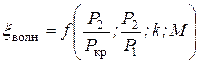
Общая оценка профильных потерь 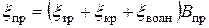
Потери трения в пограничном слое у торцевых стенок канала и потери вследствие вторичных токов
Данные потери оцениваются по аналогии с такими же потерями на сопловых решетках.
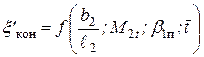
Потери от взаимодействия потока с неподвижным рабочим веществом в зазорах (потери от подсоса)
Подсасываемый пар (газ) (см. рис. 29), смешиваясь с основным потоком, создает зоны завихрения у торцевых стенок канала и, как следствие, потерю энергии.
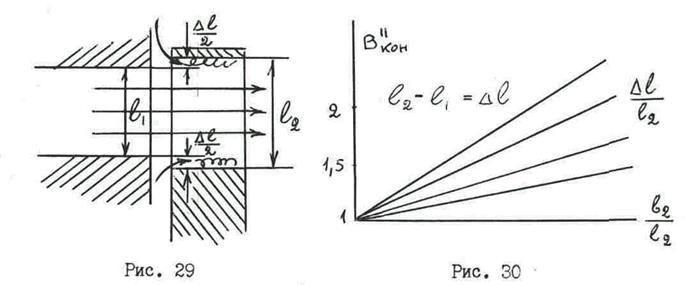
Учет подсоса производится с помощью поправочного коэффициента В который может быть определен по графику из атласа профилей. Вид графика дан на рис. 30.
В результате 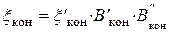
Полный коэффициент потери энергии на рабочей решетке:
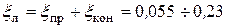
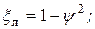
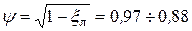
Для более точной оценки потерь энергии на рабочей решетке могут быть учтены дополнительные факторы:
1. наличие бандажной ленты,
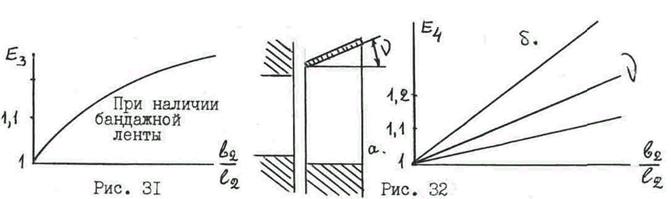
2. наличие угла раскрытия проточной части
Вид соответствующих графиков дан на рис. 31 и 32б
В результате 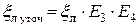
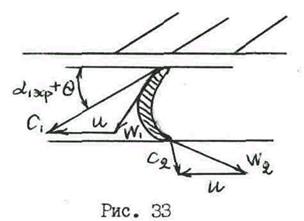
Треугольники скоростей турбинной ступени
Усилия, работа и мощность на венце рабочих лопаток – функция скоростей движения потока в межлопаточных каналах. Для расчета ступени и нахождения интересующих нас скоростей удобно пользоваться треугольниками скоростей. Их два – входной треугольник, дающий взаимосвязь скоростей на входной кромке профиля, и выходной – на выходной кромке (рис. 33).
 Рассмотрим порядок построения треугольников скоростей при наличии реакции в турбинной ступени.
Рассмотрим порядок построения треугольников скоростей при наличии реакции в турбинной ступени.
Должны быть заданы параметры пара Р0, t0, P2 и степень реакции r .
В тепловой диаграмме строится процесс расширения рабочего вещества (рис. 34) и производится расчет сопловой решетки, откуда получаются значения c1, a1эф и q (если имеет место расширение в косом срезе сопла).
Основные зависимости:
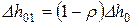
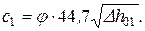
Далее на базовой линии Х-Х (рис. 35) от исходной точки 0 под углом 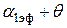 в масштабе (в 1 см – х м/сек) откладывается вектор с1 (все прочие вектора откладываются в том же масштабе). Определяется окружная скорость
в масштабе (в 1 см – х м/сек) откладывается вектор с1 (все прочие вектора откладываются в том же масштабе). Определяется окружная скорость
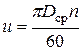
n – об/мин – число оборотов ротора,
Dср – средний диаметр облопатывания.
Вектор u пристраивается параллельно базовой линии к концу вектора c1. При соединении точки 0 с другим концом вектора u получается вектор относительной скорости входа потока на рабочую решетку W1 и относительный угол входа b1.
Предварительно оценивается коэффициент y и находится относительная скорость потока на выходе с рабочих лопаток 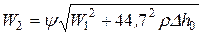 и её теоретическое значение
и её теоретическое значение 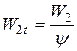 .
.
Определяется потеря энергии на рабочей решетке 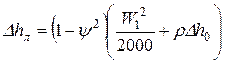 и после откладывания её на построении процесса, снимается удельный объем \/2 м3/кг (рис. 34). Критическая скорость при параметрах выходного сечения
и после откладывания её на построении процесса, снимается удельный объем \/2 м3/кг (рис. 34). Критическая скорость при параметрах выходного сечения 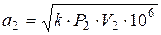 м/сек; соответствующее число Маха
м/сек; соответствующее число Маха 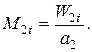
Через выражение 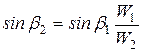 определяется угол b2.
определяется угол b2.
Далее по углам b1, b2 и числу Маха М2t из атласа подбирается стандартный профиль и по графику находится b2эф (по аналогии с сопловой решеткой).
При малом различии углов b1 и b2 профиль подбирается из группы Р, например Р-3021А. Буква Р обозначает, что профиль предназначен для рабочих решеток; первая пара цифр соответствует углу b1п, вторая – b2п, а последняя буква – характеру истечения.
Если же углы b1 и b2 различаются значительно, то профиль подбирается из группы С, например С-9015А. В этом случае первая пара цифр соответствует углу b1п, а вторая – b2п.
Профиль в обоих случаях нужно подбирать так, чтобы было максимальное соответствие углов: b2 по расчету и b2п.
Если в подобранном профиле при этом будет значительное различие угла b1п с углом b1 по построению, что приводит к появлению удара на входной кромке, то данное обстоятельство должно быть учтено при дальнейших расчетах.
Под углом b2эф от базовой линии откладывается вектор W2, к нему пристраивается вектор u и проводится замыкающий вектор c2 – вектор абсолютной скорости потока при выходе с рабочей решетки. Построив треугольники скоростей можно снять все интересующие нас составляющие.
Следует отметить, что если r = 0,5, то c1 » W2; W1 » c2; a1эф » b2эф; b1 » a2.
Построение процесса расширения в ступени в тепловой диаграмме
При построении процесса в тепловой диаграмме (рис. 36) прежде всего должны быть учтены три основные потери энергии:
потеря в соплах 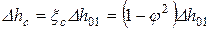
потеря на рабочих лопатках 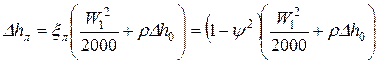
потеря с выходной скоростью – при выходе потока из каналов рабочей решетки 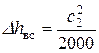
Дата добавления: 2015-06-27; просмотров: 2188;
