А —куб; б— тетрагональная дипирамида
к изображению плоскости симметрии на проекции. Как видно на рис. 35, плоскость симметрии изображается двумя параллельными линиями. В том случае если плоскости симметрии перпендикулярны к плоскости чертежа, они рисуются двумя параллельными прямыми, проходящими через центр проекции. Если плоскости наклонны или горизонтальны, они изображаются двумя параллельными дугами (рис. 36).
Поскольку на проекции будут изображены как грани, так и элементы симметрии кристалла, а точки проекций могут совпасть, не следует значки элементов симметрии рисовать мелкими или затушевывать их середину. Например, проекции верхней и нижней граней куба, изображаемые соответственно кружочком и крестиком, совпадают с осью симметрии четвертого порядка, изображаемой квадратиком. На проекции это изобразится квадратиком с нарисованными внутри него кружочком и крестиком (рис. 36, а). Проекции боковых граней так-
же совпадают с осями четвертого порядка и изображаются кружочками, расположенными внутри квадратиков (рис. 36, а).
При проектировании элементов симметрии кристаллов следует иметь в виду, что вертикальные и наклонные оси изображаются одним значком, горизонтальные— двумя значками, симметрично расположенными на противоположных сторонах диаметра. Так, на рис. 36, а одна ось четвертого порядка, расположенная вертикально к плоскости чертежа, показана одним квадратиком (в центре), то же можно сказать и об оси четвертого порядка на рис. 36, б; четыре оси третьего порядка па левом рисунке расположены наклонно, следовательно, они изображены четырьмя треугольниками. На рис. 36, б 4 осп второго порядка расположены горизонтально, поэтому каждая ось обозначена двумя эллипсами.
При составлении стереографической проекции кристалла важно правильно расположить ею внутри сферы. Об этом подробно будет сказано в конце данной главы. Здесь кратко скажем о наиболее удобном расположении кристаллов различных сингоний внутри шара при составлении стереографических проекций.
Кристаллы кубической сингоний располагают так, чтобы перпендикулярно плоскости чертежа находилась одна из осей четвертого порядка, при отсутствии таковых (например, в 28 виде симметрии кристаллов, см. табл. 1) такое же положение должна занять ось второго порядка.
При проектировании кристаллов средней категории перпендикулярно плоскости чертежа устанавливается ось шестого порядка (гексагональная сингопия), ось четвертого порядка (тетрагональная сингопия) или ось третьего порядка (тригональная сингопия).
В кристаллах ромбической сингоний ось второго порядка также располагается перпендикулярно плоскости чертежа, в моноклинной сингоний — ось второю порядка устанавливается параллельно плоскости чертежа, а плоскость симметрии — перпендикулярно к ней. В триклинпой сингонии, где нет осей и плоскостей симметрии, установка кристалла более пли менее произвольна. Рекомендуется для удобства проектирования возможно большее количество граней кристалла устанавливать вертикально.
Решение кристаллографических задач с помощью сетки Г. В. Вульфа
Методы построения простейших стереографических проекций кристаллов не претендуют на высокую точность, а преследуют цель наглядного условного отображения элементов симметрии и граней кристаллов.
В ряде случаев для изображения кристаллов и решения кристаллографических задач требуются более точные
построения. Для этих целей используются специальные стереографические сетки.
Рассмотрим устройство стереографической сетки и познакомимся с методикой решения задач с помощью одной из таких сеток, называемой сеткой Г. В. Вульфа. Мри гониометрическом измерении кристалла получают для каждой грани две сферические координаты: Рис. 37. Измерение сфериче- ф —долготу и р —полярное схих координат точки в|: расстояние, дающие точное
Долгота может иметь значение от 0 до 360°, полярное расстояние — от 0 до 180°.
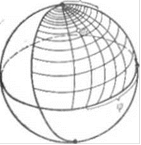
Представление о точном расположении точек можно дать, используя метод, аналогичный применяемому в географии н астрономии. Там, как нам известно, положение любой точки определяется на глобусе и фиксируется двумя координатами —долготой и широтой. Поверхность глобуса покрыта сетью линий -параллелей и меридианов, которые позволяют находить положение точки.
Таким же способом в кристаллографии определяются координаты точек. На поверхность шара наносится сеть вспомогательных параллелей и меридианов. Используя градусную сетку, получают две координаты точки, нанесенной на сфере. Одна из координат, обозначаемая греческой буквой ф, отвечает географической долготе, отсчитываемой от выбранного нулевого меридиана. Иными словами, долготу определяет угол между плоскостью пулевого меридиана н плоскостью меридиана, проходящего через заданную точку (рис. 37). Вторая координата в кристаллографии называется полярным расстоянием (р) и в отличие от географической широты отечн-тывается от полюса (рис
37). Полярное расстояние измеряется углом между полюсом шара и данной точкой,
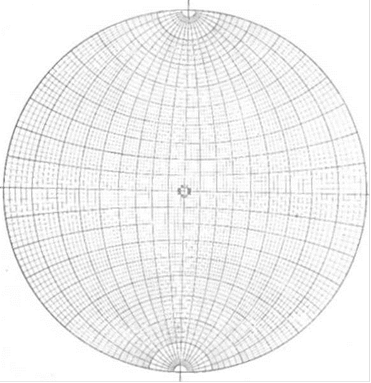
Рис. 38. Стереографическая сетка Г. В. Вульфа
т. е. р является относительно географической шпроты дополнительным углом до 90°.
При гониометрическом измерении кристалла долгота отсчитывастся по вертикальному кругу гониометра, полярное расстояние — но горизонтальному лимбу.
Наиболее широкое применение в кристаллографии получила стереографическая сетка Г. В. Вульфа. Сетка
Г. В. Вульфа представляет собой проекцию дуг меридианов и параллелей на плоскость меридиана. Точка зрения помещается на экваторе и на сетке совмещается с центром проекций. Стереографическая сетка имеет диаметр 20 см и цену деления 2°. Каждый десятый градус для удобства отсчета выделяется жирной линией (рис. 38).
Для решения кристаллографических задач с помощью сетки Г. В. Вульфа используют лист кальки, соответствующий формату сетки. Лист кальки накладывают на сетку Вульфа и в центре ее наносят точку и четыре
| 0°р | \о°<р | |
Рис. 39. Лист кальки, подготовленный к работе с сеткой Вульфа:
стрелкой показано направление отсчета долготы; через кальку проснечиваюг круг проекции и диаметры" сетки
черточки в виде креста. Черточки не доходят до точки и не пересекаются. Черточки проводят по горизонтальному и вертикальному диаметрам сетки и при начале работы с сеткой совмещают их с диаметрами, а точку — с центром проекций. С правой стороны кальки за концом горизонтального диаметра сетки проводят на кальке черточку за кругом проекций (рис. 39). Данная черточка будет в дальнейшем соответствовать нулевому значению долготы и даст начало отсчету се в направлении по часовой стрелке по кругу в интервале от 0 до 360°. Центральная точка кальки соответствует 0°р. Полярное расстояние отсчитывастся от этой точки по любому концу диаметра в направлении большого круга проекций, где р=90°, и обратно в направлении центральной точки, если полярное расстояние более 90° (до 180°). Таким образом, любая точка, расположенная на большом круге проекций, будет иметь р = 90°. Если точка расположена в центре кальки, то полярное расстояние может быть равно пулю или 180э.
Следует иметь в виду, что при решении задач все построения производятся только на кальке. Перед началом работы на кальке наносят вышеуказанные обозначения, а также отмечают 0°р вблизи центра и 0°ф рядом с пулевой риской.
Приведем примеры решения некоторых кристаллографических задач с помощью сетки Вульфа .
Задача 1. Построить стереографическую проекцию направления, заданного координатами <(; и р.
Дано некоторое направление .4 со сферическими координатами: ф= 165° и (>08".
Требуется найти стереографическую проекцию этого направлении. Задача решается следующим образом:
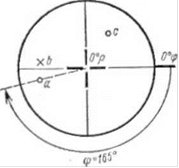
1. Рис. 40. Построение стереографической проекции направления А с координатами: <р 165°, р=68°
1)
1) Накладывают кальку на сетку Вульфа, совмещают центр кальки с центром сетки, а пулевую риску (0° ср) — с правым концом горизонтального диаметра сетки Вульфа.
1. От нулевой риски отсчитывают но часовой стрелке но кругу проекций 165° н отмечают вспомогательной черточкой-риской (рис. -10).
2. Вращением кальки совмещают найденную риску с концом ближайшего диаметра сетки (центр кальки придерживают остро заточенным карандашом в совмещенном положении с центром сетки).
3. По данному диаметру от центра сетки в сторону вспомогательной черточки отсчитывают полирное расстояние — 68" и отмечают найденную точку кружочком.
4. Возвращают кальку в исходное положение и обозначают кружочек буквой а. Пай-денная точка является стереографической проекцией направления Л.
Такое построение используют при нанесении стереографической проекции нормали к грани, или, как говорят, гномостереографиче-ской проекции грани. Аналогичный метод применяется при построении ребра или оси симметрии кристалла. В случае если полярное расстояние какого-либо направления больше 90", стереографическая проекция будет расположена в нижней полусфере. Отсчет полярного расстояния, как отмечалось, будет производиться от центра проекций в направлении круга и обратно от круга к центру. Такая проекция обозначается крестиком (рис. 40, точка Ь с координатами: ф=205°, р-124').
Задача 2 (обратная). Определить сферические координаты направлении, заданного стереографической проекцией.
Решение: 1. Вращением кальки совмещают заданную точку (стереографическую проекцию направлении) с ближайшим диаметром сетки. От центра сетки по данному диаметру отсчитывают в направлении точки сферическую координату р. Вспомогательнойчерточкой на круге проекций отмечают в данном положении конец диаметра, на котором лежит определяемая точка._ 2. Возорашают кальку в исходное положение и по кругу проекции от нулевой риски до вспомогательной черточки отсчитывают долготу ф. Таким образом, для точки с определены сферические координаты: q>=309°, р=55* (рис. 40). Задача 3. Провеет дугу большого круга через заданные стереографические проекции двух направлений.
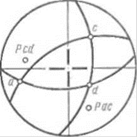
Допустим, что требуется провести дугу большою круга через стереографические проекции о и с направлений А (105°, 68") и С (309е, 55").
Решение: 1. Вращением кальки совмещают обе точки а и с с одним на вспомогательных меридианов сетки.
2. Простым карандашом обводят меридиональную дугу, соединяющую точки а и с, и возвращают кальку в исходное положение (рис. 41).'
В том случае если точки будут
Рис. 41. К решению задач располагаться на разных иолусфе-
3, 4, 5, 6, 7 pax (например, а н Ь па рис. 40),
вращением кальки приводят их на симметрично расположенные по отношению к центру сетки меридиональные дуги н обводят их простым карандашом: через точку а — сплошной линией, через точку 0 - пунктирной.
Найденная дуга большого круга может изображать гномостерео-графическую проекцию ребра, лежащего на пересечении двух граней (в этом случае заданные точки являются гномостереографнче-скими проекциями этих гранен), или стереографическую проекцию грани, если точки — стереографические проекции ребер, лежащих в плоскости данной грани.
Задача 4. Измерить угол между двумя направлениями, заданными их стереографическими проекциями (например, угол между направлениями /1 и С, см. рис. 41).
Решение: I. Вращением кальки совмещают точки о IIс с одной из меридиональных дуг сетки Вульфа (задача 3).
2. По данной дуге отсчитывают количество градусов, заключенных между точками а и с. Получают /10=113".
Измеренный угол может быть углом между нормалями к граням, сели точки а и с представляют собой их гномостерсографиче-ские проекции или углом между ребрами, если данные точки — стереографические проекции ребер.
Задача 5. Найти полюс дуги большого круга, заданной на стереографической проекции (полюсом дуги является точка, равноотстоящая от всех точек дуги на 90°).
Предположим, что требуется найти полюс дуги ас. Решение: 1. Вращением кальки совмещают данную дугу с меридиональной дугой сетки Вульфа.
2. Отсчитывают от точки пересечения данной дуги с горизонтальным диаметром в направлении к центру сетки 90° по диаметру и отмечают найденную точку кружочком.
3. Возвращают кальку в исходное положение п надписывают точку значком Р,,,-.Для найденного полюса можно найти сферические координаты: ф = 62°, р=61° (см. задачу 2). Данный полюс может представлять собой стереографическую проекцию ребра кристалла, если дуга является гномостереографической проекцией этого ребра. Полюс может быть гномостереографической проекцией грани, если данная дута — стереографическая проекция этой грани.
Аналогичным способом находится полюс дуги ей. Сто координаты: ф= 194°, р=59°.
Задача 6.(обратная). По заданному полюсу найти дугу большого круга, отвечающую его экватору.
Решение: I. Вращением кальки приводят полюс на горизонтальный диаметр сетки.
2. От точки в направлении центра сетки отсчитывают 90° и обводят карандашом соответствующую меридиональную дугу. Последняя будет искомым экватором для заданного по.чюса.
Найденная экваториальная дуга может соответствовать стереографической проекции грани в том случае, если полюс является гномостереографической проекцией ее. Дуга может соответствовать гномостереографической проекции ребра, если полюс является его стереографической проекцией.
Задача 7. Измерить угол между двумя дугами больших кругов.
Допустим, что требуется определить угол между дугами ас и ас1 (см. рис. 41).
Решение: I. Вращением кальки совмещают точку пересечения дуг а (вершину определяемого угла) с горизонтальным диаметром сетки.
2. Принимают данную вершину за полюс II проводят соответствующую ему экваториальную дугу (см. задачу 6).
3. Измеряют отрезок дуги между точками пересечения данной дуги с заданными дугами. Измеренная величина дуги состапнт величину искомого угла.
Измеренный угол при вершине а равен 65°, при вершине с - -75", при вершине й— 116*.
Измеренные углы представляют собой углы между соответствующими гранями при условии, что заданные дуги больших кругов — стереографические проекции этих граней.
Кристаллографические символы. Закон рациональных отношений
Многообразие внешнего облика кристаллов, встречающихся в природе, обусловлено различными сочетаниями, или комбинациями, простых форм. Определив элементы симметрии кристалла, количество простых форм и вид симметрии кристалла, не всегда получают однозначное представление о кристалле. Одни класс симметрии может включать в себя несколько различных по внешнему виду кристаллов. Например, кристаллы кварца могут встречаться в виде гексагональной дшшрамиды
или комбинации гексагональной дииирамиды с гексагональной призмой (см. рис. 23, / и 2). Разные но внешнему виду, оба кристалла имеют одинаковую формулу симметрии: Ь6<5127РС. То же можно сказать о кристаллах циркона (см. рис. 24, /, 3, 4, 5). Все четыре формы относятся к одному и тому же виду симметрии тетрагональной сингонии: ЈЧ/.25РС, а кристаллы под номерами 4 и 5 даже состоят из одних и тех же простых форм — двух тетрагональных призм и тетрагональной дииирамиды.
Таким образом, определение вида симметрии или даже наличие стереографической проекции кристалла не всегда дает нам однозначное представление о внешнем облике кристалла.
Для более точной характеристики кристалла определяют взаимное расположение его граней в пространстве по отношению к определенным координатным осям и некоторой исходной грани. Для определения грани применяются так называемые кристаллографические символы. Понятие о кристаллографических символах вытекает из второго закона кристаллографии, открытого в 1784 г. французским исследователем Р. Ж. Гаюи. Этот закон называется законом рациональных отношений или законом параметров, именуемым также законом целых чисел.
Закон рациональных отношений гласит: положение всякой грани может быть определено тремя целыми числами, если за оси координат выбраны направления трех ребер кристалла и за единицы измерения взяты отрезки, отсекаемые на этих осях одной из граней кристалла.
Нередко дастся и другая формулировка данного закона— «двойные отношения параметров (отрезков), отсекаемых двумя любыми гранями кристалла на трех пересекающихся его ребрах, равны отношениям целых и сравнительно малых чисел» .
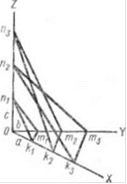
Возьмем три непараллельных ребра кристалла, пересекающихся в точке О, и обозначим их ОХ. ОУ. 01. Выбранные три ребра примем за координатные оси (рис. 42). Покажем три грани кристалла, пересекающие координатные оси: к\Ш\П\, к2т-2п?, и к$тлП2. Отрезки, отсекаемые этими гранями на осях, называются параметрамй граней. Например, для грани 1г\ГП\П\параметрами являются Ок\, О/П] и Оп\. Примем параметры этой грани за единицы измерения по соответствующим осям (Ок\— по оси X, Ош\—по оси У, Оп\ —по оси 2). В этом случае параметры остальных граней кристалла будут рациональными числами.
Рпс. 42. Схема координатных осей, пересекаемых гранями кристалла
Выбранная грань называется единичной гранью, а ее параметры — осевыми единицами. Эти осевые единицы взяты за единицы измерения — единичные отрезки.
Следует иметь в виду, что эти параметры могут быть не равны друг другу (например, на рис. 42 у грани к\Шхпх параметры Ок\-фОш\ФОп\). Положение данной грани обозна
обозначается символом (111). Символ обозначает, что грань отсекает по каждой оси по одной осевой единице.
В кристаллографии принято так располагать кристаллографические оси: X — на себя — положительное значение, от себя - отрицательное; У— вправо — положительное значение, налево - - отрицательное, 1 — вверх — положительное значение, вниз — отрицательное. Осевые единицы обозначают: по X — а, по У - - Ь, но 1 — с.
Выбор единичной грани задаст масштаб по каждой оси. В нашем случае при выбранной единичной грани к\Ш\П\ ее параметрами будут а, Ь, с. Положение грани кчШчПг определится параметрами 2а, 2Ь, Зс, для грани кзт3П2 — За, 36, 2с.
Чтобы представить положение каждой грани в пространстве, следует знать (помимо направления осей), как параметры, задающие масштабы по разным осям, относятся друг к другу.
В общей форме отношение параметров любой грани можно выразить как ра:цЬ:тс, где р, а и /- — целые числа.
Для каждого определяемого кристалла необходимо выбрать направление кристаллографических осей и од-
| (Названиепростоя формы | См | л | Количество граней | |
| Гексаэдр (куб) | (1 | 0! | ft | |
| Октаэдр | |1 | } | ||
| Тетраэдр | Ў1 | II | 412 | |
| Ром бододекаэлр | И | 2! | ||
| Пентагон-додекаэдр | 1* | k | ||
| Тетрагексаэдр | {А | к | ?,1 | |
| Гсксоктаэдр | (Л | 1: | 1) |
T а б л и ц а 3 Символы простых форм кубической синюнни
ну из наклонных к ним граней в качестве единичной грани. Эту операцию называют установкой кристалла. Иногда при установке кристалла некоторые грани оказываются параллельными одной или двум координатным осям. В этом случае их параметры по данным осям будут равны бесконечности (ос).
Разобранный способ обозначения граней при помощи параметров предложен немецким ученым X. Вейссом (1818). В 1839 г. английским ученым У. Миллером была рекомендована более удобная система обозначений. Вместо величин р, q и /- он предложил брать обратные
величины — — —• Отношение этих правильных Р Ч г
дробей можно выразить и целыми числами — : —: —=
_ Р Я г
эти три числа принято называть индексами грани и обозначать буквами латинского алфавита Ii, Ii, I. Заключенные в круглые скобки индексы составляют символ грани (hkl).
В большинстве случаен индексы граней представлены числами меньше 10. Индексы в круглых скобках не разделяются знаками препинания. Исключение делается, когда один из индексов равен пли больше 10. При этом индексы отделяются точками, например (10-3-2). Над индексами ставят знак (—) минус в том случае, если грань отсекает соответствующий отрезок по отрицательному направлению оси. Принято следующее расположение индексов: по осп X — h, но оси Y—k, по оси Z —/. В таком порядке индексы и пишутся в круглых скобках для обозначения символа грани.
Как перейти от параметров к индексам? Для единичной грани f<imlnl (см. рис. 42) индексы Л, k, I равны единице, так как величины р, q, г равны единице (каждая).
Следовательно, отношения —, — — также сосгав-
Р ч г
ляют единицу. Таким образом, символ грани 1:хт\П\ будет (111). Для грани k2tn2n3 (см. рис. 42) параметры
составляют 2, 2 и 3. Индексы грани к,тгп,~ : —: — =
1 г 1 8 2 2 3 = 3:3:2. Отсюда символ этой грани (3 3 2). Грань
кз/п3Пй имеет индексы—:—:—=2:2:3 и символ ее
Л 3 2
(2 2 3). 58
Если грань параллельна какой-либо кристаллографической осп, то индекс ее по этой оси будет равен нулю, так как — = 0. Если в кристалле у грани два иное
дскса равны нулю, то третий всегда равен единице. Например, грань параллельна осям X и У, а по оси 7. отсекает две осевые единицы. Следовательно, параметры грани со : со : 2, а индексы— : —: -—=0:0:2. Сокра-
Дата добавления: 2015-06-27; просмотров: 2708;
