Стереографические проекции кристаллов

В кристаллографии для пространственного изобра­жения изучаемых кристаллов, их элементов симметрии и элементов ограничения используются различные про­екции. Наиболее часто применяются стереографическая (от греч. «стерсос» — пространственный, объемный) II гномостереографическая (от греч. «гномон» — перпенди­куляр) проекции.

Для построения проекции кристалла последний поме­щается в центр шаровой сферической поверхности. Гра­ни и ребра кристалла продолжаются до пересечения с шаровой поверхностью и изображаются так: грани — в виде дуг, ребра —в виде точек. Такая проекция получи­ла название стереографической. Для более наглядного изображения кристаллов используют гномостереографи-ческую проекцию. В данном случае проектируется не грань, а перпендикуляр к ней, проекции ребер замени ются нормальными к ним плоскостями. При гномостерсо-графическом проектировании грани дают на сфере точ­ки, а ребра—дуги.

Рассмотрим принципы построения стереографической проекции и простейшие случаи стереографического про­ектирования кристаллов.

Рис. 33. Схема построения стереографических проек­ций направлении и плос­кости

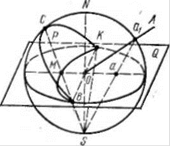
Возьмем шаровую поверхность произвольного диа­метра с центром О (рис. 33). Точка О —это центр про­екций, а шаровая поверхность—шар проекций. Прове­дем через центр проекций плоскость Q, называемую плоскостью проекций. При пересечении сферической по­верхности получается круг проекций. Он соответствует экватору шара и является большим кругом (в отличие от малых кругов, получающихся при пересечении шара плоскостями, не проходящими через его центр). Плос­кость проекций раздели­ла шар на северное и юж­ное полушария, или на верхнюю и нижнюю полу­сферы. Вертикальный ди­аметр NS называется осью проекций. Точка N— северный полюс, точка S — южный полюс. Одну из этих точек, обычно юж­ный полюс, выбирают за точку зрения.

Для изображения сте­реографической проекции направления или плоско­сти необходимо перенес­ти их параллельно самим себе до прохождения их

через центр проекций (точка О). Например, направление ОА дает при пересечении его со сферой точку й\. Соеди­нив проекцию направления АО на сферической поверхно­сти, т. с. ai с точкой зрения 5 лучом зрения Sa_lt получаем на горизонтальном диаметре точку а, являющуюся сте­реографической проекцией направления ОА на плоско­сти. Если какое-либо направление пересекает нижнюю (южную) полусферу, за точку зрения принимают север­ный полюс. Итак, проекции направлений изображаются точками.

Плоскость Р при пересечении шаровой поверхности дает дугу ВСК, являющуюся дугой большого круга. Сое­диним все точки дуги лучами зрения с южным полюсом. Получаем из множества лучей проектирующий конус, который при пересечении с плоскостью проекций даст Дугу КМВ. Эта дуга, опирающаяся па концы диаметра, есть стереографическая проекция плоскости Р. Имеется

теорема, согласно которой стереографическая проекция круга представлена также крутом. Таким образом, сте­реографические проекции плоскостей изображаются кру­говыми дугами.

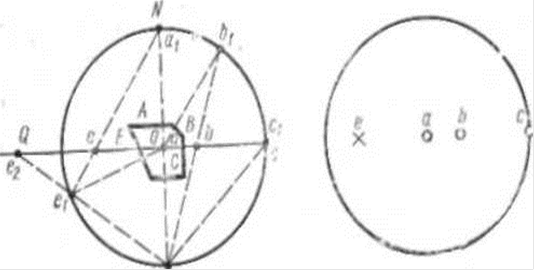
Рассмотрим теперь, как проектируются кристаллы методом стереографических проекций. Возьмем какой-либо кристаллический многогранник и совместим центр его, например центр тяжести, с точкой О, являющейся центром проекций. Произвольным радиусом опишем во­круг данного центра сферическую поверхность — шар тальную плоскость. Такие проекции называются гномо-стереографическими (грсч. «гномон» — перпендикуляр). Из построения, приводимого на рис. 34, /, видно, что гномостереографические проекции граней изображаются в виде точек. Эти точки располагаются внутри круга проекций, если нормали к граням пересекают верхнюю полусферу (грани А, в и С). Пели пересечение шара происходит в нижней полусфере (например, нормаль к грани Е дает точку <?,), то проекция точки на горизон-

Рис. 34. Гвоностерсографйчсские проекции гранейЛ. В, С. Е (/) и изображение этих проекций на плоскости(} (II, вид сверху)

О

А

С

Рис. 35. Условные обозначения элементов симметриина стереографической проекции:

Ось симметрии второго порядка; 2 —ось симметрии третьего порядка: 3 — ось симметрии четвертого порядка: 4 — ось симметрии шестого порядка; 5 — инверсионная ось четвертого порядка; 6 — инверсионная ось шестого порядка; 7 — плоскость симметрии; 8 — центр симметрии

проекций (рис. 34). Рассечем шар проекций горизонталь­ной плоскостью проекций С?, проходящей через точку О. Спроектируем грани кристалла сначала па шаровую поверхность, а затем на плоскость проекций. Для этого из центра проекций О на грани кристалла опустим пер­пендикуляры и продолжим их до пересечения с шаровой поверхностью. На рис. 34 для иллюстрации построения взять! четыре грани: А, В, С и Е. Па сферической поверх­ности мы получим четыре точки: для грани А—а\, для грани В—Ьи для грани С—С\ и для грани Е—е\. Далее перенесем все найденные точки на горизонтальную плоскость проекций. Принимаем южный полюс шара 5 за точку зрения и соединяем се лучами зрения со всеми четырьмя точками, расположенными на сфере. Получа­ются новые четыре точки, лежащие на плоскости С?,— а, Ь, с и <?2-Эти точки — стереографические проекции нор­малей соответствующих граней кристалла на горизон­тальную плоскость располагается за кругом проекций. Чтобы избежать этого неудобства, за точку зрения в данном случае принимают северный полюс N. Тогда проекция и для грани Е оказывается внутри круга про­екций (рис. 34, точка е). Для отличия проекций граней, нормали к которым пересекают верхнюю полусферу, от нормалей к граням, пересекающих нижнюю полусферу принято: первые обозначать на плоскости кружочками, вторые —крестиками (рис. 34, //).

Таким образом, при проектировании горизонтальных граней их проекции попадают в центр круга проекций (грань А, рис. 34). проекции вертикальных граней изо­бражаются на большом круге проекций (грань С, рис. 34), наклонные грани проектируются внутри круга проекций (грани В и Л, рис. 34).

Следует иметь в виду, что чем круче наклон грани к оси проекций, тем ближе се проекция к кругу, чем поло-

•п.

же — тем ближе се проекция к центру проекций О.

При построении стереографической проекции кри­сталла для его более полного отображения практикует­ся нанесение на проекцию элементов симметрии данного кристалла. Условились элементы симметрии изображать следующими значками (рис. 35). Характер обозначений понятен из приводимою рисунка. Пояснение следует дать

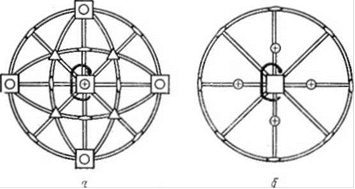
Рис. 36. Стереографические проекции элементов симметрии и гра­ней кристаллов: