Методы расчета волноводно-щелевых антенн 3 страница

В плоскости электрического вектора Е диаграмма не­сколько уже, чем в плоскости магнитного вектора Н, что объясняется разным законом изменения амплитуды поля в раскрыве в плоскостях Е и Н.

Если в качестве исходной величины для расчета раз­меров задан коэффициент направленного действия (к. н. д.), то дополнительно указывается соотношение размеров раскрыва (например, квадратный раскрыв) или соотношение ширины диаграммы направленности в плоскостях Е и Н. Выбор размеров раскрывов по к. н. д. может быть выполнен при использовании графи­ков рис. 6.8-t-6.10 § 6.7. Размеры горловины рупора совпадают с размерами поперечного сечения волноводов и дополнительного определения не требуют.

Длину руйора (см. рис. 6.1) характеризуют два раз­мера: h — расстояние от раскрыва до горловины рупора, одинаковое в плоскостях Е и Н, R_E и R_n — расстояние от раскрыва до точки, в которой сходятся ребра пирами­дального рупора в плоскостях Е и Н соответственно. ' При выбо|ре длины пирамидального рупора г-^вия

обеспечить дв-? условия: 1) допустимую фаз<^^ения ^п0

icre возбуж-

154 ^J

ку в раскрыве и 2) правильную стыковку рупора с пи­тающим волноводом. Максимальная фазовая ошибка в раскрыве фМакс определяется геометрическими размерами рупора и ее допустимая величина должна удовлетворять условиям:

Из (6.11) и (6.12) получаются необходимые соотноше­ния для определения длины рупора в плоскостях Н и Е:

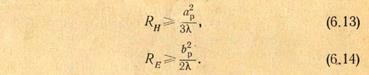
С другой стороны, из треугольников в плоскостях Н Е (см. рис. 6.1) следует

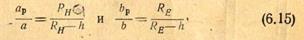
откуда размеры рупора для осуществления стыковки связаны следующим соотношением:

Длину рупора рассчитывают в следующем порядке. Определяют длину рупора в одной из плоскостей, на­пример R_H (или R_e), заменив в формуле (6.13) или (6.14) неравенство равенством, затем по формуле (6.16) находят длину рупора в другой плоскости R_E (или R_H). Если найденное значение R_E (или R_H) не удовлетворяет неравенству (6.14) или (6.13), то в первую очередь опре­деляют длину R_e (или R_H), а затем R_H (или R_E)■

В секториальном рупоре стыковка с питающим вол­новодом может быть обеспечена при любой длине рупо­ра, поэтому при выборе длины рупора должно учиты­ваться только условие обеспечения допустимой фазовой ошибки. Для секториального рупора, расширяющегося в плоскости Н, должно выполняться условие (6.13),

а для рупора, расширяющегося в плоскости Е, — усло­вие (6.14).

Длина оптимального конического рупора связана с диаметром его раскрыва 2г и длиной волны соотноше­нием

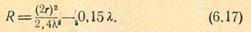
Если в раскрыве рупора применяется какое-либо фа- зовыравнивающее устройство, рупор может быть сделан значительно короче. Например, при установке в раскры­ве рупора линзы длина рупора берется равной фокусно­му расстоянию линзы.

6.4. Расчет возбуждающего устройства

Рассмотрим некоторые варианты переходов от коак­сиальной линии к волноводу. В большей части перехо­дов используется электрическая связь, хотя при некото­ром усложнении конструкции может быть реализован

также метод магнитной связи.

На рис. 6.3—6.5 изображено несколько примеров электриче­ской связи возбуждающего устройства с волноводом.

Критерием согласования воз­буждающего устройства с волно­водом служит режим бегущей волны в коаксиальном питаю­щем фидере, т. е. равенство входного сопротивления возбуж­дающего устройства Z_BX волно­вому сопротивлению фидера

На рис. 6.3 изображено наи­более распространенное устрой­ство зондового типа в виде не­симметричного штыря, располо­женного параллельно электриче­ским силовым линиям. Спе­циально подбирая длину штыря I и расстояние от штыря до зако­рачивающей стенки Zi, можно обеспечить требуемое согласова­ние. Диэлектрическая шайба, фиксирующая положение шты­ря в волноводе, является де-

талью коаксиального соединения. Диаметр наружного проводника около шайбы увеличивается для того, чтобы сохранить волновое сопротивление в области, заполнен­ной диэлектриком, равным р_ф. Длина шайбы берется равной четверти волны в диэлектрике. На графике для примера приведена кривая изменения к. с. в. в полосе частот для устройства, согласованного на волне К = ^=9,5 см. По сравнению с другими типами возбуждаю-

щих устройств рассматриваемый зондовый переход имеет несколько меньшую механическую и электрическую прочность и узкую частотную полосу.

Более жесткий и точный метод крепления зонда по­средством диэлектрической втулки показан схематически на рис. 6.4,а.

Одним из первых способов перехода от коаксиальной линии к волноводу с достаточно жестким креплением зонда и двумя органами регулировки является устрой­ство, приведенное на рис. 6.4,6. Центральный проводник коаксиальной линии 'проходит через волновод и нагру­жается иа верхнем конце закороченным коаксиальным шлейфом. Изменением длины этого шлейфа и длины ко- роткозамкнутой части волновода можно добиться пол­ного согласования. Описываемое устройство узкополос­ное и его целесообразно применять при работе на фикси­рованной волне или как настраиваемое устройство.

На рис. 6.4,в показана схема зондового перехода с поперечным стержнем, обеспечивающим вполне на-

/

Дежное крепление вертикального штыря; на рисунке показана диафрагма, улучшающая согласование.

Для работы в полосе частот может использоваться модифицированный зондовый переход. Известно, что для диапазонной работы должны использоваться толстые вибраторы. Увеличение диаметра возбуждающего штыря

уменьшает реактивную часть входного сопротивления и расширяет рабочую полосу частот, в которой обеспечи­вается согласование (рис. 6.4,г). Для уменьшения тор­цевой емкости между ниж­ним торцом штыря и стен­кой волновода толстый штырь должен иметь кони­ческий переход к среднему проводу коаксиала. Такое устройство обеспечивает по­лосу в несколько процентов.

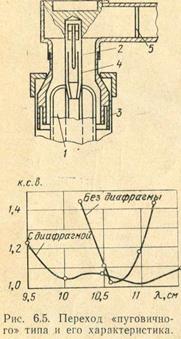
Дальнейшим развитием диапазонного зонда являет­ся коаксиальный переход «пуговичного» типа (рис. 6.5). Центральный провод­ник коаксиальной линии оканчивается на противопо­ложной стороне волновода утолщением соответствую­щего размера и изменением формы, благодаря чему обеспечивается согласова­ние полных сопротивлений и увеличивается мощность пробоя. На рис. 6.5 приведен пример выполнения связи 10-см магнетрона 1 через коаксиальную линию 2 с вол­новодом. Внешние проводники соединены при помощи коаксиального дроссельного соединения 3. Центральные проводники соединены штекерной фишкой 4, сконструи­рованной так, чтобы обеспечить пружинящий контакт. Вследствие сложной геометрической формы размеры перехода очень критичны и желаемые характеристики трудно воспроизвести. Характеристики перехода при­ведены там же на рис. 6.5.

Более эффективным способом расширения полосы
является включение в волновод реактивных согласую­щих элементов, например индуктивных диафрагм 5 (рис. 6.5). Выбрав соответствующим образом место вклю­чения и величину реактивного согласующего элемента, можно добиться достаточно хорошего согласования в по­лосе частот 10—20%. Подробнее этот метод описан в [ЛО 15].

Приведем некоторые соображения по расчету зондо- вого перехода (см. рис. 6.3).

Входное сопротивление штыря в волноводе, так же как несимметричного вибратора в свободном пространст­ве, является в общем случае комплексной величиной. Активная часть входного сопротивления зависит в ос­новном от длины штыря, реактивная — от длины и тол­щины. В отличие от свободного пространства входное сопротивление штыря в волноводе зависит от структуры поля в волноводе вблизи штыря.

Расчет реактивной составляющей входного сопротив­ления дает неточные результаты и проводить его не име­ет смысла. Для обеспечения согласования реактивная составляющая входного сопротивления должна быть равна нулю. Активную составляющую входного сопро­тивления можно считать равной сопротивлению излуче­ния штыря в волноводе RОна должна быть равна волновому сопротивлению фидера

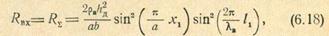
где Ij рекомендуется брать равным Яв/4. При наличии отраженной волны в прямоугольном волноводе сопротивление штыря несколько изменяется: где !i рекомендуется выбирать из условия равенства

Сопротивление излучения штыря в прямоугольном

реактивных частей проводимостей справа и слева от штыря, а именно:

(6.20)

В приведенных формулах приняты следующие обо­значения: а и b — размеры поперечного сечения волно­вода; xi — положение штыря на широкой стенке волно­вода, чаще всего штырь располагается в середине ши­рокой стенки, т. е. Xi = a/2; k — расстояние от штыря до закорачивающей стенки волновода; Z\ — расстояние от штыря до ближайшего узла напряжения; к. б. в. — ко­эффициент бегущей волны в волноводе; Я_в — длина вол­ны в волноводе; р_в — волновое сопротивление волновода

— действующая высота штыря в волно­воде, геометрическая высота которого /, определяется по формуле

Задаваясь величинами Xi и 1_Ь можно по формулам (6.18), (6.19) и (6.21) найти высоту штыря /, при кото- . рой получается требуемое R_Bx-

Для полного согласования в конструкциях должны предусматриваться два органа регулировки. Например, можно регулировать высоту штыря / и положение за­корачивающей стенки в волноводе U (см. рис. 6.3) или размеры и 5 (см. рис. 6.4,6). В ряде случаев для упро­щения конструкции ограничиваются одной регулиров­кой и допускают некоторое рассогласование в питаю­щем коаксиале.

6.5. Расчет коэффициента отражения

Отражение в рупорной антенне возникает в двух сече­ниях: в раскрыве рупора (Г,) и в его горловине (Г₂).

Рассмотрим коротко каждый из коэффициентов отраже­ния. Коэффициент отражения от раскрыва Г, является^ком-

плексной величиной; его модуль и фаза зависят от раз- 160

меров раскрыва. Строгое решение задачи для открытого конца волновода, зажатого между двумя бесконечными плоскостями, проведенное Вайнштейном Л. А., позво­ляет установить, что модуль коэффициента отражения уменьшается с увеличением размеров раскрыва, а фаза приближается к нулю.

Приближенно модуль коэффициента отражения от раскрыва для основного типа волны может быть опре­делен из соотношения

где к = 2тс/Я — волновое число;

— постоянная распространения в прямоугольном вол­новоде, поперечное сечение которого равно раскрыву рупора;

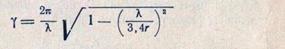
— постоянная распространения в круглом волноводе, диаметр которого равен диаметру раскрыва коническо­го рупора.

Коэффициент отражения по длине рупора от раскры­ва к горловине изменяется не только по фазе, но и по амплитуде. При размерах раскрыва в несколько длин волн коэффициент отражения Ti можно считать прибли­зительно равным нулю.

Коэффициент отражения Ti от открытого конца пря­моугольного волновода (23X10) мм² на волне 3,2 см, из­меренный экспериментально, равен

Рассмотрим коэффициент отражения от горловины ру­пора Г₂.

При определении"коэффициента Г₂ предполагается, что в рупоре установилась бегущая волна. Задача решается методом сшивания полей в месте соединения волновода U-479 т
и pyinopa. Приравнивание полей в центре сечения волно­вода в плоскости соединения дает следующее выражение для эквивалентного сопротивления:

После замены функций Ханкеля 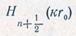их асимптоти­

ческими выражениями, а также принимая, что углы рас- крыва pyinopa невелики и ctgao—1/W можно из форму­лы (6.23) получить

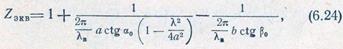
где а и 6 —размеры поперечного сечения волновода; 2ао и 2|3₀ — углы раскрыва рупора в плоскостях Н и Е соот­ветственно.

. Подставив в выражение (6.25) значение Z9KB, найденное по формуле (6.24), получим искомую величину коэффи­циента отражения от горловины рупора. Сочленение ipynopa с волноводом будет самосогласо­ванным, если

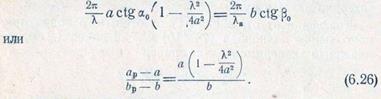
Коэффициент отражения Г₂ через эквивалентное сопро­тивление выражается весьма просто

В последнее соотношение не входит длина рупора, однако она должна быть достаточно велика, чтобы вы­полнялось условие малости углов раскрыва.

Наличие отраженной волны в волноводе несколько изменяет входное сопротивление возбуждающего штыря. .162

Рассогласование штыря с коаксиальным фидером может быть устранено дополнительным уточнением размеров- или экспериментальной подстройкой. Обычно для этой цели используют индуктивную диафрагму, расположен­ную в волноводе вблизи горловины рупора. Более широ­кополосное согласование можно получить, применяя ди­электрическую пластину, расположенную в раскрыве рупора. Толщина пластины подбирается из условия получения полной компен­сации отраженной волны. Хорошее согласование обес­печивает диэлектрический кожух, закрывающий рас­крыв рупора при соответст­вующем выборе размеров.

В том случае, если гене­ратор имеет волноводный вы­ход и весь питающий тракт состоит из отрезков волно­вода, то отражение от рас- крыва и горловины будет проходить к выходу генера­тора, складываясь с отраже­ниями от других неоднородностей в тракте (фланцев, изгибов и пр.). Допуски, задаваемые на изготовление отдельных элементов тракта, определяют разброс коэф­фициентов отражения от одних и тех же элементов в условиях серийного производства.

Из опыта известно, что .модули коэффициента отра­жения имеют сравнительно небольшой разброс, фазы ко­эффициента отражения от экземпляра к экземпляру из­меняются весьма значительно.

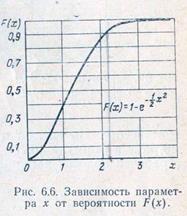
Можно считать фазы местных коэффициентов отра­жения подчиненными закону равной вероятности. Ожи­даемый модуль суммарного коэффициента отражения на ныходе длинного тракта определяется по формуле

где |Гг| —модуль коэффициента отражения от г-й неод­нородности; /г — число неоднородностей, вносящих о^ра-

жение в тракт; х — пара* метр, определяемый по гра­фику рис. 6.6 [ЛО 17].

Величина F(x), отложен­ная по оси ординат, озна­чает вероятность появления модуля суммарного коэффи­циента отражения при ис­следовании на фиксирован­ной частоте множества эк­земпляров одного и того же тракта.

При работе в полосе ча­стот ожидаемый коэффи­циент отражения на входе тракта будет больше, чем при работе на фиксирован­ной частоте. На рис. 6.7 приведена зависимость пара­метра х в формуле (6.27) от параметра k, связанного с рабочей полосой частот следующим соотношением:

I о

лоса частот.

График построен для вероятности F(x)= 0,9. Таким образом, можно утверждать с вероятностью 0,9 (т. е. 90 экземпляров из 100), что максимальный ко­эффициент отражения на входе тракта в полосе частот будет не больше |Г₂|, рассчитанного по формуле (6.27). Для других значений F(x) необходимые кривые приве­дены в 'справочнике [JIO 17].

6.6. Расчет диаграммы направленности

Исходной величиной, определяющей диаграмму на­правленности рупора (см. рис. 6.1), является поле E_s в его раокрыве. Для пирамидального и секториального рупоров функция, описывающая поле в раскрыве, имеет

При расчете диаграммы направленности антенны по­ле в раскрыве можно принимать синфазным (= 0>, так как в правильно спроектированном рупоре фазовая ошибка не изменяет существенно диаграмму направлен­ности. Амплитудное распределение в раскрыве, как ука­зывалось выше, принимается совпадающим с полем в поперечном сечении питающего волновода.

Диаграмма направленности рупора F(0, tp) может быть приближенно рассчитана по формуле Кирхгофа, используемой в оптике для скалярных величин.

В плоскости Н, т. е. в 'плоскости XZ, выражение для диаграммы направленности секториального или пирами­дального рупора, полученное но формуле Кирхгофа, имеет следующий вид [JIO 13]:

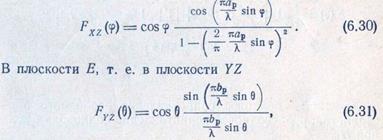
где углы 0 и ср отсчитываютея от нормали к раскрыву , рупора соответственно в плоскостях Е и Я.

Те же формулы (6.30) и (6.31) с учетом поправки на векторный характер электромагнитного поля будут вы­глядеть следующим образом:

(По формулам (6.30)—'(6.33) определяют поле излу­чения в первом приближении, исходя из условия, что ио­ле в раскрыве равно невозмущенному полю, какое было бы <в бесконечно длинном рупоре. Полученный результат может быть несколько уточнен, если учесть, что от рас- крыва отражается волна основного типа #_i0. Поле в рас' крыве определяется в этом случае суперпозицией оря- мой и отраженной волн.

С учетом коэффициента отражения Г для диаграммы направленности получается следующее выражение [J10 1]: в плоскости Н

где г; = 120л; — волновое сопротивление свободного про­странства; рю — волновое сопротивление волновода с вол­ной #ю

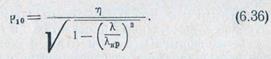
Все приведенные выше формулы дают приближенные результаты, так как они исходят из приближенного зна­чения поля в раскрыве, определяемого без учета влия­ния внешнего поля. Расчетные и экспериментальные диаграммы в пределах сравнительно небольших углов хорошо совпадают.

Результаты расчетов поля по вышеприведенным фор­мулам близки друг iK другу. Таким образом может быть использована любая пара формул: (6.30), (6.31), или (6.34), (6.35), или (6.32), (6.33). При этом результаты расчетов будут достоверными для главного и ближайших боковых лепестков.

Диаграмма направленности конического рупора опре­деляется по полю в его раскрыве. Можно считать, что амплитудное распределение в раскрыве рупора совпа­дает с законом изменения амплитуды поля в поперечном 166 сечении круглого волновода с волной #ц, фаза поля ме­няется по квадратичному закону. Для упрощения расче­тов поле в раскрыве можно принять синфазным, анало­гично допущениям, принимаемым в пирамидальных рупорах.

На основе формулы Кирхгофа получаются следую­щие 'выражения для диаграммы направленности 'кониче­ской рупорной антенны с учетом коэффициента отраже­ния от раскрыва:

в плоскости Н

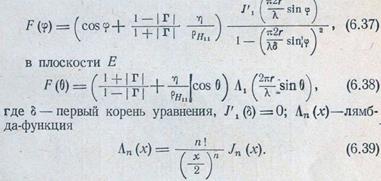
Для раскрыва в несколько Я можно принять Т~0. Для расчета поля излучения открытого конца прямо­угольного и круглого волновода приведенные выше фор мулы (6.34), (6,35) и '(6.37), (6.38) не вполне пригодны. Это объясняется тем, что формулы Кирхгофа дают до­статочно точные результаты при размерах раскрыва, превышающих длину волны в несколько раз. Для ма­леньких рупоров или открытых 'концов волновода можно пользоваться диаграммами направленности, приведенны­ми в [JIO 9], построенными на основе экспериментальных данных.

6.7. Коэффициент направленного действия и коэффициент усиления

Качество антенн характеризуется 'коэффициентом усиления антенны, равным произведению 'коэффициента направленного действия (к. н. д.) на коэффициент полез­ного действия (к. п. д.) антенны.

Для рупорных антенн можно считать, что мощность потерь значительно меньше мощности излучения, благо­даря чему к. п. д. антенны можно принять равным еди­нице.

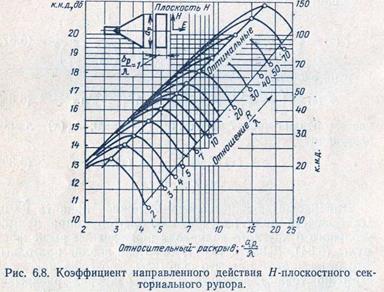
На рис. 6.8 и 6.9 для секториальных рупоров, расши­ряющихся в плоскости Я и в плоскости Е, построены зависимости к. н. д. от величины широкой стенки раскры- ва для различных длин рупора. На графиках приведены значения к. н. д. при узких стенках раскрыва, равных длине волны. Для определения к. «. д. при других раз-

мерах узкой стенки найденное ио графикам значение следует умножить на величину узкой стенки, взятую в долях 'волны (6_Р/Я или a_v/k).

Коэффициент направленного действия D₀ пирами­дального рупора можно также получить с помощью при­веденных графиков по формуле

имея в виду, что по вертикальным осям на указанных гра­фиках отложены фактически величины

Значения каждой из скобок берется непосредственно из графиков рис. 6.8 и 6.9. В точках максимума 'кривых

J 68

R/X = const к. н. д. равен примерно 0,&D_MaKC, рассчитан­ного то формуле _А

где S — площадь раскрыва.

Прямая, проходящая через максимумы кривых /?A=oonst на графиках рис. 6.8 и 6.9, соответствует оптимальным размерам рупоров, так как получающаяся в этом случае в раскрыве рупора фазовая ошибка ока-

зывается в пределах допустимой. Уменьшение длины рупора по сравнению с оптимальной приводит к умень­шению к. н. д., а увеличение конструктивно нежела­тельно.

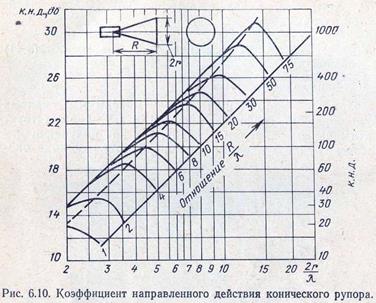
На рис. 6.10 построены зависимости к. н. д. кониче­ского рупора с волной Н_п от диаметра раскрыва и дли­ны. Пунктирная кривая соответствует оптимальным раз­мерам рупора.

6.8. Диапазонность рупорной антенны

Диапазонность антенны обусловливается допустимым изменением основных параметров антенны: диаграммы направленности, 'коэффициента усиления, а также изме­нением входного сопротивления или согласования, ха­рактеризуемого коэффициентом бегущей волны в питаю­щей линии.

Диапазонность рупорной антенны зависит от диапа- зонности основных ее элементов — рупора, волновода и возбуждающего устройства (если в конструкции имеется переход от коаксиального кабеля к волноводу).

Диапазонность волновода ограничивается условием распространения в волноводе только волны основного типа [см формулу (6.1) и рис. 6.2].

Волновод допускает примерно (полуторное перекры­тие по диапазону, а именно а и Адекс=^(1,67 Для 'рупора критической волны не существует, поэтому рупор не накладывает ограничений на условия распро­странения электромагнитных волн в широком диапазоне частот. Однако с изменением длины волны изменяется ширина диаграммы направленности и, следовательно, 170
к. н. д. антенны. На крайних частотах диапазона необ­ходимо определить к. н. д. по графикам, приведенным в § 6.7, имея в виду, что размеры антенны, взятые в до­лях волны, по диапазону изменяются. При полуторном перекрытии по диапазону, который обеспечивается вол­новодом, изменение к. н. д. несколько превышает 20%'. Известен [ЛО. 9] метод расчета размеров рупоров, кото­рые обеспечивают примерно постоянный к. н. д. в широ­ком диапазоне частот за счет уменьшения его 'макси­мального значения.

(Вероятное значение коэффициента отражения в пол­новодном тракте при работе в полосе частот может 'быть найдено по формулам ¹(6.27), (6.28) и графику рис. 6.7.

.Диапазонность возбуждающего устройства зависит от его конструкции. В § 6.4 рассмотрены некоторые вариан­ты возбуждающих устройств, предназначенных для ра­боты в полосе частот. Метод расчета широкополосных переходов от коаксиальной линии к волноводам, как ука­зывалось выше, изложен в работе [ЛО. 15].

6.9. Методика расчета рупорных антенн

В технических заданиях на проектирование рупорных антенн требуется обычно обеспечить или определенный коэффициент усиления или определенную ширину диа­граммы направленности.

Расчет рупорной антенны в основном сводится к рас­чету геометрических размеров рупоров и возбуждающе­го его волновода, а также к расчету диаграммы направ­ленности, коэффициента направленного действия и дру­гих параметров.

При проектировании рупора по заданному коэффи­циенту усиления можно рекомендовать следующий поря­док расчета.

1. На заданную длину волны рассчитывают или бе­рут рекомендованные размеры поперечного сечения вол­новода, возбуждающего рупор. Размеры волновода 'вы­бираются из условия распространения только основного типа волны (#ю — в прямоугольном волноводе и Нц — в круглом волноводе).

2. Размеры поперечного сечения 'волновода опреде­ляют одновременно размеры горловины рупора.

3. 'Коэффициент полезного действия рупора полагают равным единице и,считают, что коэффициент усиления равен к. н. д. антенны. По заданному к. н. д. из графи­ков определяют оптимальные размеры рупора. Если рупор еекториальный с расширением в плоскости Н (или в плоскости Е), то пользуются графиками на рис. 6.8 (или рис. 6.9), из которых определяют длину рупора и ширину раскрыва в долях волны. Если рупор пирами­дальный, то его коэффициент направленного действия определяют по формуле (6.40) и графикам рис. 6.8 и 6.9. Соотношение между сомножителями (X/6_PD_H) и (h/a_vD_E) можно в общем случае выбирать произвольно.'Если же помимо коэффициента усиления накладываются требо­вания на диаграмму направленности, то нужно учиты­вать, что более узкая диаграмма получается в той пло­скости, в которой раскрыв больше.

4. После определения параметров рупора проверяют фа­зовую ошибку в раскрыве по формуле (6.11)Д;ля плоскости Н и по формуле (6.12) для плоскости Е. Если фазовая

ошибка превышает допустимую ^--------------- в плоскости Е и

тс — в плоскости H^j , то размеры рупора следует не­сколько изменить. При каждом изменении следует про­изводить проверку фазовых ошибок.

5. Расчет диаграммы направленности в двух взаим­но перпендикулярных плоскостях осуществляют в пред­положении синфазного поля в раскрыве антенны по формулам (6.30) и (6,31) или (6.32) и (6.33), а с учетом коэффициента отражения от раскрыва—по формулам (6.34) и (6.35). При этом следует учитывать, что в пре­делах главного лепестка указанные формулы дают ре­зультаты, близкие друг к другу и к экспериментальным данным, при определении боковых лепестков погреш­ность расчета по всем указанным формулам возрастает.