Стационарность и эргодичность СС.
СС X(t) называется стационарным в узком смысле, если его плотности вероятности любого порядка n не изменяются при сдвиге всей группы сечений на произвольную величину t0, то есть статистические свойства СС не зависят от начала отсчета времени.
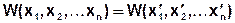
где 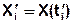
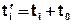
Следствия:
1) Для такого колебания
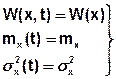 Не зависят от времени.
Не зависят от времени.
2) двумерная плотность не зависит от моментов, в которых берутся сечения, а зависит лишь от разности моментов времени, в которых берутся сечения.
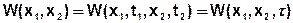 ;
; 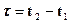
СС Х(t) называется стационарным в широком смысле, если его математическое ожидание и дисперсия не зависят от времени, а АКФ, 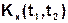 зависит лишь от разности моментов времени, в которых берутся сечения, т.е.
зависит лишь от разности моментов времени, в которых берутся сечения, т.е.
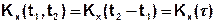 ,где
,где 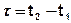
Второму определению удовлетворяет более широкий класс сигналов.
Сигнал, стационарный в узком смысле, всегда является стационарным в широком смысле. Обратное утверждение в общем случае неверно.
Стационарный случайный сигнал Х(t) называется эргодическим, если его любые неслучайные числовые характеристики могут быть найдены не только путем усреднения по ансамблю реализаций, но и путем усреднения по времени его единственной реализации 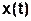 .
.
Усреднение по времени обозначается чертой сверху.

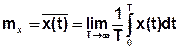
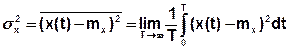
Примечание:
1) Усреднение должно происходить за бесконечно большой промежуток времени, т.е. реализация должна быть бесконечно большой.
2) У эргодического сигнала все реализации «похожи».
Заметим, что в нашем курсе чаще всего будут встречаться стационарные эргодические сигналы.
Физический смысл неслучайных числовых характеристик эргодического СС электрического происхождения.
Математическое ожидание mx – постоянная составляющая СС.
Дисперсия 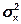 - средняя мощность переменной составляющей СС, выделяемая на единичном сопротивлении.
- средняя мощность переменной составляющей СС, выделяемая на единичном сопротивлении.
σх – средне квадратичное отклонение СС (эффективное значение СС).
М2 – второй начальный момент.
М2= 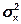 +
+ 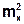 - полная средняя мощность CC.
- полная средняя мощность CC. 
Дата добавления: 2015-06-22; просмотров: 1135;
