Принцип измерения расстояния

Этот принцип основан на прямолинейности и постоянстве скорости распространения радиоволн. С большой степенью точности скорость распространения можно считать равной с = 300 000 км/сек. Значит, измерив время 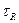, за которое сигнал проходит расстояние от приемо-передатчика до объекта и обратно, получим:

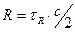. (8.3)

Полезно запомнить такие соотношения: время распространения 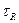= 1 мкс соответствует расстоянию R = 150 м; расстоянию R = 1 км соответствует время 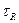= 6,7 мксек.

Однако, измерив расстояние, мы ещё не устанавливаем местоположение объекта, а лишь определяем некоторую поверхность, на которой находится цель – поверхность положений цели. При измерении дальности поверхностью положения является сфера радиусом R с центром в точке расположения приемо-передатчика. Если к тому же известно, что цель находится в плоскости горизонта, то измеренному значению 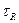соответствует линия положения в виде окружности радиуса R.

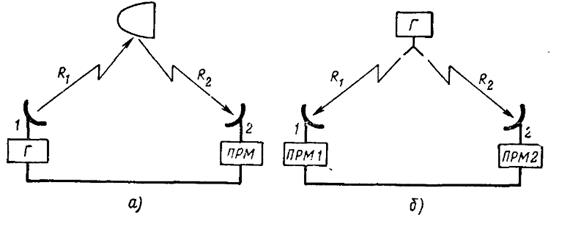
Рис. 8.1. Суммарно-дальномерная (а) и разностно-дальномерная (б) системы.

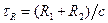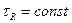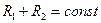Приемник и передатчик радиолокационной системы могут быть разнесены (рис. 8.1, а). В этом случае измеренный интервал времени соответствует сумме расстояний от объекта до приемного (ПРМ) и передающего (Г) пунктов . Если , то . Это выражение определяет в пространстве поверхность положения в виде эллипсоида вращения или линию положения – эллипс – на земной поверхности (рис. 8.2, а). Пункты расположения приемника и передатчика являются фокусами эллипсоида. Такая радиолокационная система называется суммарно-дальномерной.

Можно построить и систему, в которой излучения объекта принимаются двумя разнесенными пассивными РЛС и измеряется разность прихода сигналов 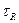(рис. 8.1, б). Такая разностно-дальномерная система измеряет разность расстояний 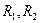между объектом и пунктами приема. Фиксированному значению 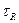соответствует и фиксированная разность 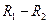. В этом случае поверхность положения, определяемая уравнением 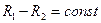, представляет собой гиперболоид вращения, а линия положения – гиперболу (рис. 8.2, б).

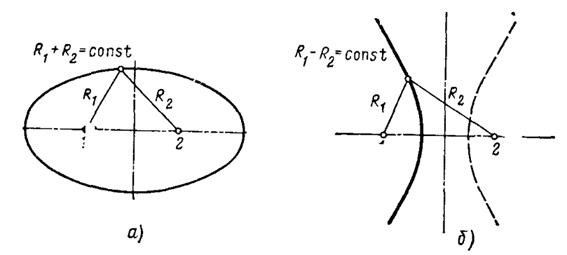
Рис. 8.2. Линии положения суммарно-дальномерной (а) и разностно-дальномерной (б) систем