ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

ВИЗУАЛЬНЫЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА В МОРЕ

Глава 1

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1.1 Основные понятия, связанные с определением места судна

Основным автономным методом получения текущих координат места судна является счисление его пути. Погрешности элементов счисления (курса и скорости судна, дрейфа, направления морского течения и его скорости) обусловливают погрешность счисления, которая накапливается с течением времени. Возникает необходимость периодической коррекции результатов счисления. Эта коррекция производится посредством определения места судна (ОМС) с использованием физических величин, не связанных с элементами счисления.

Рассмотрим общий подход к решению задачи определения места судна в море и основные положения общей теории навигации, относящейся к данной проблеме.

Основными понятиями обшей теории навигации, связанными с ОМС, являются понятия:

· навигационного параметра,

· навигационного ориентира,

· навигационной функции,

· навигационной изолинии,

· линии положения,

· градиента навигационного параметра.

Навигационный параметр — это физическая величина, опреде­ляющая положение судна в пространстве. В общем случае он обозначается символом U. К навигационным параметрам относятся: направления, углы, расстояния, разности расстояний, скорости изменения расстояний и т. д.

Измерение навигационных параметров производится относи­тельно материальных объектов или условных линий, положение и направление которых в пространстве известны.

Объекты с отличительными признаками и известным положением, наблюдаемые для ОМС, называются морскими навигацион­ными ориентирами. Ориентиры, которые наблюдатель видит невооруженным глазом или с помощью оптических средств, называются визуально наблюдаемыми наземными ориентирами.

Измеренные значения навигационного параметра (навигационных параметров) позволяют, после их исправления поправками и соответствующей обработки, получить координаты места судна. Процесс измерения и обработки навигационных параметров, ре­зультатом которых является место судна, получаемое в виде коор­динат или в виде точки на морской навигационной карте, называется определением места судна или обсервацией.

Отметим, что обсервацией часто называют и само место судна, полученное в результате измерения и обработки навигационных параметров.

Измеренный судовым навигационным прибором и исправленный всеми поправками навигационный параметр называется обсервованным и обозначается символом U0.

Математическое выражение, устанавливающее связь между навигационным параметром и координатами места судна, называется навигационной функцией U = f (j, l).

Линия, каждая точка которой соответствует одному и тому же значению навигационного параметра, называется навигационной изолинией.

Таким образом, измерив навигационный параметр U, можно заключить, что судно в момент измерения находится на навигаци­онной изолинии U = U (j, l), соответствующей этому параметру.

Наиболее распространенным в судовождении навигационным параметрам соответствуют следующие навигационные изолинии:

при измерении пеленга на ориентир — изоазимута, линия, в каждой точке которой угол Л между истинным меридианом и направлением по кратчайшему расстоянию на ориентир есть величина постоянная;

при измерении пеленга с ориентира на судно — ортодромия, линия, пересекающая меридиан ориентира под измеренным углом A0;

при измерении расстояния — изостадия, сферическая окружность, проведенная из точки, в которой расположен ориентир, радиусом, равным измеренному расстоянию D;

при измерении горизонтального угла или разности азимутов - изогона, кривая (при малых расстояниях до ориентиров — окружность), проходящая через ориентиры и вмещающая измеренный угол;

при измерении высоты светила — круг равных высот (высотная изолиния), сферическая окружность, проведенная из географического места светила (полюса освещения) как из центра, радиусом, равным зенитному расстоянию светила;

при измерении разности расстояний до ориентиров, расположенных в разных точках, — сферическая гипербола, в каждой точке которой разность расстояния DD до рассматриваемых ориентиров есть величина постоянная;

при измерении глубин — изобата, линия, соединяющая точки с равными глубинами.

Существуют также навигационные изолинии, соответствующие постоянным значениям скорости сближения с искусственным спутником Земли (изодола), скорости изменения расстояния, пеленга и т. п.

Уравнения и форма навигационных изолиний, как правило, сложны. Это вызывает определенные затруднения с прокладкой изолиний на навигационных картах и приводит к необходимости замены изолинии отрезком прямой. Отрезок прямой, которым заменен ограниченный по длине отрезок изолинии, называется линией положения. Этой линией может быть отрезок касательной к изолинии или хорда, соединяющая две точки изолинии.

Каждой точке пространства соответствует определенное значение навигационного параметра U. Таким образом, можно говорить о поле навигационного параметра. Это поле является скалярным. Важная характеристика этого поля - градиент навигационного параметра. Он обозначается символами gradU и характеризует направление и максимальную скорость изменения навигацион­ного параметра.

Градиент навигационного параметра — вектор, направленный по нормали к навигационной изолинии и характеризующий скорость изменения навигационного параметра по этому направлению. По абсолютной величине он равен пределу отношения приращения навигационного параметра dU к соответствующему смещению изолинии dn:

Lim 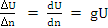(1.1)

при n —> 0,

где U— навигационная функция. Из выражения (1.1) следует, что

dn =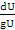

Перейдя к конечным приращениям, можно записать

Dn = 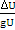(1.2)

где DU = (U2 – U1) — разность значений параметра двух соседних изолиний (разность их оцифровок, U2 > U1); D — кратчайшее расстояние от заданной точки изолинии U1 = const до изолинии U2 = const.

Из этого соотношения можно заключить, что градиент является коэффициентом пропорциональности между изменением навигационного параметра и смещением линии положения.

Если DU - случайная погрешность навигационного параметра, характеризуемая средней квадратической погрешностью mП, то средняя квадратическая погрешность положения навигационной изолинии или линии положения mЛП определяется выражением

mЛП = 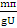(1.3)