Оптической разностью хода волн.

На основании (19.7) и (19.8) получим связь между разностью фаз и оптической разностью хода интерферирующих волн:

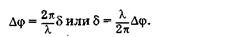(19.9)

Используя законы сложения колебаний (см. § 5.3.) и соотно­шение (19.9), получаем условия максимума и минимума ин­тенсивности света при интерференции — соответственно

Следовательно, максимум при интерференции наблюдается в тех точках, для которых оптическая разность хода равна цело­му числу длин волн (четному числу полуволн), минимум — в тех точках, для которых оптическая разность хода равна нечетному числу полуволн.

^{____________________________}

¹ Схематичность рис. 19.3 не позволяет показать разные среды распространения для различных волн.

² Полезно заметить, что так как 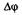не зависит от времени, то слагаемые волны являются когерентными.

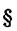19.2. Интерференция света в тонких пластинках (пленках). Просветление оптики

Образование когерентных волн и интерференция происходят также при попадании света на тонкую прозрачную пластинку или пленку.

Пучок света падает на плоскопараллельную пластинку (рис. 19.4). Луч 1 из этого пучка попадает в точку А, частично отража­ется (луч 2), частично преломляется (луч AM). Преломленный луч испытывает отражение на нижней границе пластинки в точке М. Отраженный луч, преломившись в точке В, выходит в первую среду (луч 3). Лучи 2 и 3 образованы от одного луча, поэтому они когерентны и будут интерферировать.

Найдем оптическую разность хода лучей 2 и 3. Для этого из точ­ки В проведем нормаль ВС к лучам. От прямой ВС до встречи лу­чей их оптическая разность хода не изменится, линза или глаз не внесут дополнительной разности фаз. До расхождения в точке А эти лучи в совокупности с другими, параллельными им, не пока­занными на рис. 19.4, формировали луч 1 и поэтому, естественно, имели одинаковую фазу. Луч 3 прошел расстояние 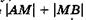в пластинке с показателем преломления п, луч 2 — расстояние 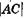в воздухе, поэтому их оптическая разность хода

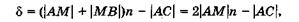(19.12)

так как 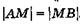. Согласно закону преломления,

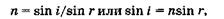(19.13)

где i — угол падения, г — угол преломления.

Из 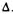АМО находим: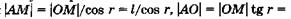 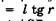(/ — толщина пластинки). Из 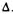АСВнаходим

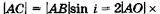
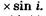
Учитывая эти равенства, а также (19.13), получаем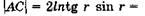

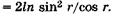
Тогда оптическая разность хода ин­терферирующих волн равна

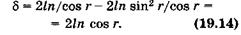
Рис.19.4

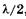В формуле (19.14) не учтено одно важное обстоятельство. Опыт показывает, что при отражении света от среды оптически более плотной, т. е. с большим показателем преломления, фаза волны изменяется на п, что соответствует [см. (19.9)] изменению оптиче­ской разности хода на , т. е. при отражении света от среды оптически более плотной происходит «потеря полволны»¹.

Если бы оба луча 2 vs. 3 теряли пол волны, то это не изменило бы выражения для 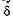(19.14). Однако луч 2 отражается от среды опти­чески более плотной (точка А) и теряет полволны, а луч 3 отража­ется от среды оптически менее плотной (точка М), его фаза при этом не изменяется. С учетом потери полволны оптическая раз­ность хода

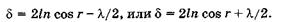(19.15)

Так как 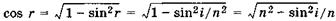, то d можно выразить и через угол падения:

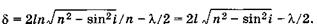(19.16)

Для максимума интерференции [см. (19.10), (19.16)] имеем

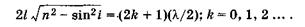(19.17)

Для минимума интерференции [см. (19.11), (19.16)] имеем²

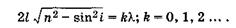(19.18)

Формулы (19.17) и (19.18) соответствуют интерференции в от­раженном свете. Интерференция в проходящем через пластинку свете показана на рис. 19.5; изо­бражены только те лучи, которые необходимы для понимания яв­ления. Читатель может самостоятель­но вывести соответствующие фор-­
мулы и убедиться, что для этого случая (19.17) соответствует мини­муму интерференции, а (19.18) —
максимуму. С учетом закона со­хранения энергии это понятно, так как интерференция есть перерас- пределение световой энергии: падающий поток перераспределяется пластинкой на отраженный и

Рис. 19.5

проходящий (поглощением здесь пре­небрегаем), причем если отраженный максимален, то проходящий минимален, и наоборот.

Интерференция при отражении наблюдается более отчетливо, чем в проходящем свете, что обусловлено существенным различи­ем интенсивностей отраженного и проходящего лучей. Если при­нять, что на границе раздела прозрачных сред отражается около 5% падающей энергии, то

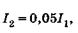(19.19)

где 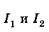— интенсивности лучей 1 м 2 соответственно (см. рис.19.4). Интенсивность луча 3 с учетом двукратного преломления и однократного отражения равна

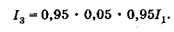(19.20)

Из (19.19) и (19.20) имеем

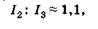(19.21)

что означает приближенное равенство амплитуд интерферирую­щих лучей при отражении: условие минимума соответствует по­чти полной темноте. Делая аналогичный расчет для проходящего света (рис. 19.5), получаем

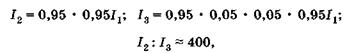
или для амплитуд

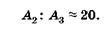(19.22)

Из (19.22) видно, что в проходящем свете интерферируют вол­ны с существенно различными амплитудами, поэтому максиму­мы и минимумы мало отличаются друг от друга и интерференция слабо заметна.

Проанализируем зависимости (19.17) и (19.18).

Если на тонкую плоскопараллельную пластинку под некото­рым углом падает параллельный пучок монохроматического из­лучения, то, согласно этим формулам, пластинка в отраженном свете выглядит яркой или темной.

При освещении пластинки белым светом условия максимума и минимума выполняются для отдельных длин волн, пластинка станет окрашенной, причем цвета в отраженном и проходящем свете будут дополнять друг друга до белого.

При падении монохроматического света на пластинку переменной толщи­ны каждому значению I соответствует
свое условие интерференции, поэтому пластинка пересечена светлыми и тем­ ными линиями (полосами) — линиями равной толщины. Так, в клине это система параллельных линий (рис. 19.6), в воздушном промежутке между линзой и пластинкой — кольца (кольца Ньютона).

Рис. 19.6

При освещении пластинки переменной толщины белым светом получаются разноцветные пятна и линии: окрашенные мыльные пленки, пленки нефти и масла на поверхности воды, переливча­тые цвета крыльев некоторых насекомых и птиц. В этих случаях не обязательна полная прозрачность пленок.

Особый практический интерес имеет интерференция в тонких пленках в связи с созданием устройств, уменьшающих долю све­товой энергии, отраженной оптическими системами, и увеличи­вающих, следовательно, энергию, поступающую к регистрирую­щим системам — фотопластинке, глазу и т. п. С этой целью по­верхности оптических систем покрывают тонким слоем оксидов металлов так, чтобы для некоторой средней для данной области спектра длины волны был минимум интерференции в отражен­ном свете. В результате возрастает доля прошедшего света. По­крытие оптических поверхностей специальными пленками назы­вают просветлением оптики, а сами оптические изделия с такими покрытиями — просветленной оптикой.

Если на стеклянную поверхность нанести ряд специально по­добранных слоев, то можно создать отражательный светофильтр, который вследствие интерференции будет пропускать или отра­жать излучение в определенном интервале длин волн.

¹ Для циклических процессов не имеет значения, уменьшается или уве­личивается фаза на к, поэтому равноценно было бы говорить не о потере, а о приобретении полволны, однако такая терминология не употребляется.

² Для того чтобы при максимумах и минимумах сохранить для k те же значения (0, 1, 2 и т. д.), формулу (19.16) для 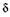записываем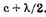

§ 19.3. Интерферометры и их применение. Понятие об интерференционном микроскопе

Интерференцию света используют в специальных приборах — интерферометрах — для измерения с высокой степенью точнос­ти длин волн, небольших расстояний, показателей преломления веществ и определения качества оптических поверхностей.

На рис. 19.7 изображена принципиальная схема интерферо­метра Майкельсона, который относится к группе двухлучевых, так как световая волна в нем раздваивается¹ и обе ее части, прой­дя разный путь, интерферируют.

Луч 1 монохроматического света от источника S падает под уг­лом 45° на плоскопараллельную стеклянную пластинку А, задняя поверхность которой полупрозрачна, так как покрыта очень тон­ким слоем серебра. В точке О этот луч расщепляется на два луча 2 и 3, интенсивность которых приблизительно одинакова.

Луч 2 доходит до зеркала /, отражается, преломляется в пластине А и частично выходит из пластины — луч 2'. Луч 3 из точки О идет к зеркалу //, отражается, возвращается к пластине А, где частично от­ражается, — луч 3'. Лучи 2' и 3', попадающие в глаз наблюдателя, когерентны, их интерференция может быть зарегистрирована.

Обычно зеркала I и II располагают так, что лучи 2 и 3 от рас­хождения до встречи проходят пути одинаковой длины. Чтобы и оптическую длину путей сделать одинаковой, на пути луча 3 уста­навливают прозрачную пластину В, аналогичную А, для компен­сации двух путей, пройденных лучом 2 через пластину А. В этом случае наблюдается максимум интерференции.

Если одно из зеркал сдвинуть на расстояние 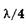, то разность хода лучей станет к/2, что соответствует минимуму, произойдет смещение интерференционной картины на 0,5 полосы². Если зеркало от первоначального положения переместить на расстоя­ние к/2, то оптическая разность хода
интерферирующих лучей изменится на к, что соответствует максимуму, произойдет смещение интерференци­онной картины на целую полосу. Та­кая связь между перемещением зер­кала и изменением интерференцион­ной картины позволяет измерять длину волны по перемещению зерка­ла и, наоборот, перемещение по длине волны.

Интерферометр Майкельсона применяют для измерения пока­зателя преломления. На пути лучей 2 и 3 устанавливают одинако­вые кюветы К (показаны штриховыми линиями на рис. 19.7), од­на из которых наполнена веществом с показателем преломления n1 а другая — с п₂. Оптическая разность хода лучей

Рис. 19.7

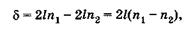(19.23)

где I — длина однократного пути луча в среде, заполняющей кю­веты; так как лучи проходят кювету дважды, то расстояние равно 21. Предположим, что вследствие этой разности хода интерферен­ционная картина смещается на 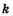полос, тогда

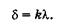(19.24)

Приравнивая (19.23) и (19.24), получаем

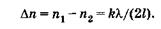(19.25)

Если считать, что смещение на 0,1 полосы (к = 0,1) может быть зафиксировано, то, например, при 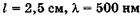имеем

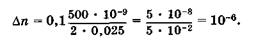
Как видно, интерференционный рефрактометр (интерферо­метр, приспособленный для измерения показателя преломления) способен фиксировать изменения показателя преломления в шес­том знаке после запятой.

Интерференционный рефрактометр применяют, в частности, с санитарно-гигиеническими целями для определения содержания вредных газов.

С использованием интерферометра Майкельсон доказал неза­висимость скорости света от движения Земли, что явилось одним из опытных фактов, способствовавших созданию специальной те­ории относительности.

Сочетание двухлучевого интерферометра и микроскопа, полу­чившее название интерференционного микроскопа, используют в биологии для измерения показателя преломления, концентра­ции сухого вещества и толщины прозрачных микрообъектов.

Принципиальная схема интерференционного микроскопа пока­
зана на рис. 19.8. Луч света, как и в ин­терферометре, в точке А раздваивается,один луч проходит через прозрачный микрообъект М, а другой — вне его. В точке Д лучи соединяются и интерферируют, по результату интерференции судят об измеряемом параметре.

Рис. 19.8

1 1 Строго говоря, вследствие многократных отражений может образо­ваться более чем два луча, однако их интенсивности незначительны

2 2 Вследствие разных углов падения лучей из S на пластину А или не­ строгой перпендикулярности зеркал I и II интерференционная картина практически всегда представлена полосами (полосы равного наклона или равной толщины соответственно). Этот вопрос подробно не рассматрива­ется.

§ 19.4. Принцип Гюйгенса—Френеля

Объяснение и приближенный расчет дифракции света можно осуществить, используя принцип Гюйгенса—Френеля.

Согласно Гюйгенсу, каждая точка волновой поверхности, ко­торой достигла в данный момент волна, является центром элемен­тарных вторичных волн, их внешняя огибающая будет волновой поверхностью в последующий момент времени (рис. 19.9; S_l и S₂ — волновые поверхности соответственно в моменты t_t и t₂; t₂ > tj).

Френель дополнил это положение Гюйгенса, введя представ­ление о когерентности вторичных волн и их интерференции. В таком обобщенном виде эти идеи получили название принципа Гюйгенса—Френеля.

Для того чтобы определить результат дифракции в некоторой
точке пространства, следует рассчитать, согласно принципу Гюй­
генса—Френеля, интерференцию вторичных волн, попавших в эту
точку от различных элементов волновой по­верхности. Для волновой поверхности произ­вольной формы такой расчет достаточно сложен, но в отдельных случаях (сферическая или плоская волновая поверхность, симметричное расположение точки относительно волновой поверхности и непрозрачной преграды) вычисления сравнительно

Рис. 19.9

просты. Волновую поверх­ность при этом разбивают на отдельные участ­ки (зоны Френеля), расположенные определенным образом, что упрощает математические операции.

§ 19.5. Дифракция на щели в параллельных лучах

На узкую длинную щель, расположенную в плоской непроз­рачной преграде MN, нормально падает плоскопараллельный пу­чок монохроматического света (рис. 19.10; АВ = а — ширина ще­ли; L — собирающая линза, в фокальной плоскости которой рас- -положен экран Э для наблюдения дифракционной картины).

Если бы не было дифракции, то световые лучи, пройдя через щель, сфокусировались бы в точке О, лежащей на главной оптиче­ской оси линзы. Дифракция света на щели существенно изменяет явление.

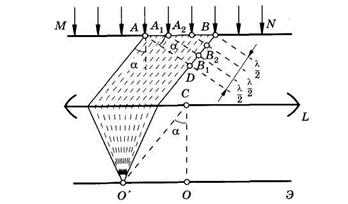
Рис. 19.10

Будем считать, что все лучи пучка света исходят от одного уда­ленного источника¹ и, следовательно, когерентны. АВ есть часть волновой поверхности, каждая точка которой является центром вторичных волн, распространяющихся за щелью по всевозмож­ным направлениям. Изобразить все эти вторичные волны невоз­можно, поэтому на рис. 19.10 показаны только вторичные волны, распространяющиеся под углом а к направлению падающего пуч­ка и нормали к решетке. Линза соберет эти волны в точке О' экра­на, где и будет наблюдаться их интерференция. (Положение точ­ки О' получают как пересечение с фокальной плоскостью побоч­ной оси СО' линзы, проведенной под углом а.)

Чтобы узнать результат интерференции вторичных волн, про­делаем следующие построения. Проведем перпендикуляр AD к направлению пучка вторичных волн. Оптические пути всех вто­ричных волн от AD до О' будут одинаковыми, поскольку линза не вносит добавочной разности фаз между ними, поэтому та разность хода, которая образовалась у вторичных волн к AD, будет сохра­нена и в точке О'.

Разобьем BD на отрезки, равные l/2. В случае, показанном на рис. 19.10, получено три таких отрезка: \ВВ₂\ = \В₂В_г\ = \B₁D\ = = l/2. Проведя из точек В₂ и В1 прямые, параллельные AD, разде­лим АВ на равные зоны Френеля: \АА_г\ = \А1А₂\ = \А₂В\. Любой вторичной волне, идущей от какой-либо точки одной зоны Френеля, можно найти в соседних зонах соответствующие вторичные волны такие, что разность хода между ними будет 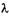/2. Например, вторичная волна, идущая от точки А₂ в выбранном направлении, проходит до точки О' расстояние на 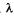/2 больше, чем волна, иду­щая от точки A1, и т. д. Следовательно, вторичные волны, идущие от двух соседних зон Френеля, погасят друг друга, так как раз­личаются по фазе на .

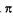Число зон, укладывающихся в щели, зависит от длины волны 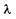и угла 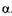. Если щель АВ можно разбить при построении на не­четное число зон Френеля, a BD — на нечетное число отрезков, равных 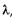/2, то в точке О' наблюдается максимум интенсивнос­ти света:

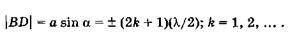(19.26)

Направление, соответствующее углу а = 0, также отвечает макси­муму, так как все вторичные волны придут в О в одинаковой фа­зе.

Если щель АВ можно разбить на четное число зон Френеля, то наблюдается минимум интенсивности света:

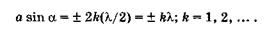(19.27)

Таким образом, на экране Э получится система светлых (мак­симум) и темных (минимум) полос, центрам которых соответству­ют условия (19.26) и (19.27), симметрично расположенных влево и вправо от центральной (а = 0), наиболее яркой, полосы. Интен­сивность I остальных максимумов быстро убывает по мере удале­ния от центрального максимума (рис. 19.11).

Если щель освещать белым светом, то на экране Э [см. (19.26), (19.27)] образуется система цветных полос, лишь центральный максимум будет сохранять цвет падающего света, так как при а = 0 усиливается свет всех длин волн.

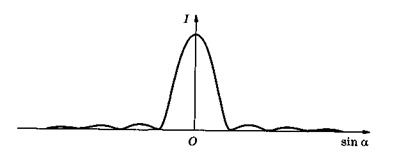
Рис. 19.11

Дифракция света, как и интерференция, связана с перераспре­делением энергии электромагнитных волн в пространстве. В этом смысле щель в непрозрачном экране является не просто системой, ограничивающей поступление светового потока, но перераспреде­лителем этого потока в пространстве.

Чтобы понять влияние соотношения между шириной щели и длиной волны на возможность наблюдения дифракционной кар­тины, рассмотрим некоторые частные случаи:

1) 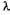<< а. Представив формулу для максимумов в виде

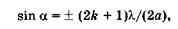
имеем sin a ~ 0 практически для всех максимумов, и дифракция при этом не наблюдается. Этот случай соответствует достаточно широкой, по сравнению с длиной волны, щели. Так, например, не удается осуществить дифракцию в комнате при прохождении све­та через окно;

2) 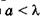. На основании (19.27) для первых минимумов, которые ограничивают центральную светлую полосу, можно записать

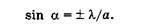
Отсюда следует, что при заданном условии sin а формально пре­вышает единицу, чего не может быть. Практически в этом случае вместо системы максимумов и минимумов весь экран будет слабо освещен.

¹ Практически точечный источник можно расположить в фокусе лин­зы, не показанной на рис. 19.10, так, что от линзы будет распространять­ся параллельный пучок когерентных волн.

§ 19.6. Дифракционная решетка. Дифракционный спектр

Дифракционная решетка — оптическое устройство, пред­ставляющее собой совокупность большого числа параллельных, обычно равноотстоящих друг от друга, щелей.

Дифракционную решетку можно получить нанесением непроз­рачных царапин (штрихов) на стеклянную пластину. Непроцарапанные места — щели — будут пропускать свет; штрихи, соот­ветствующие промежутку между щелями, рассеивают и не пропус­кают света. Сечение такой дифракционной решетки (о) и ее условное обозначение (б) показанына рис. 19.12. Суммарную ширину щели а и промежутка Ъ между щелями называют постоянной или периодом дифракционной ре­шетки:

Рис. 19.12 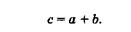(19.28)

 

Если на решетку падает пучок когерентных волн, то вторич­ные волны, идущие по всевозможным направлениям, будут ин­терферировать, формируя дифракционную картину.

Пусть на решетку нормально падает плоскопараллельный пу­чок когерентных волн (рис. 19.13). Выберем некоторое направле­ние вторичных волн под углом а относительно нормали к решет­ке. Лучи, идущие от крайних точек двух соседних щелей, имеют разность хода 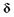= А'В'. Такая же разность хода будет для вторич­ных волн, идущих от соответственно расположенных пар точек соседних щелей. Если эта разность хода кратна целому числу длин волн, то при интерференции возникнут главные максиму­мы, для которых выполняется условие 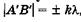, или

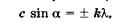(19.29)

где 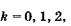... — порядок главных максимумов. Они расположены симметрично относительно центрального (k = 0, а = 0). Равенство (19.29) является основной формулой дифракционной решетки¹.

Между главными максимумами образуются минимумы (доба­вочные), число которых зависит от числа всех щелей решетки. Выведем условие для добавочных минимумов. Пусть разность хо­да вторичных волн, идущих под углом а от соответственных то­чек соседних щелей, равна 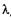/N, т. е.

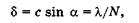(19.30)

где N — число щелей дифракционной решетки. Этой разности хо­да 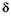[см.(19.9)]отвечает разность фаз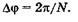

 

 

Рис. 19.13

 

Если считать, что вторичная волна от первой щели имеет в мо­мент сложения с другими волнами нулевую фазу, то фаза волны от второй щели равна 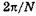, от третьей — 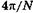, от четвертой — 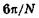и т. д. Результат сложения этих волн с учетом фазового раз­личия удобно получить с помощью векторной диаграммы: сумма N одинаковых векторов напряженности электрического поля, угол (разность фаз) между любыми соседними из которых есть 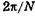, равна нулю. Это означает, что условие (19.30) соответствует минимуму. При разности хода вторичных волн от соседних щелей 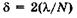или разности фаз 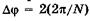будет также получен минимум интерференции вторичных волн, идущих от всех ще­лей, и т. д.

В качестве иллюстрации на рис. 19.14 изображена векторная диаграмма, соответствующая дифракционной решетке, состоя­щей из шести щелей: E1 Е₂ и т. д. — векторы напряженности электрической составляющей электромагнитных волн от первой, второй и т. д. щелей. 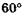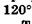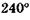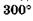Возникающие при интерференции пять до­бавочных минимумов (сумма векторов равна нулю) наблюдаются при разности фаз волн, приходящих от соседних щелей, в (а), (б), 180° (в), (г) и (д).

Так, можно убедиться, что между центральным и каждым пер­вым главным максимумами имеется N - 1 добавочных минимумов, удовлетворяющих условию

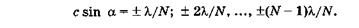(19.31)

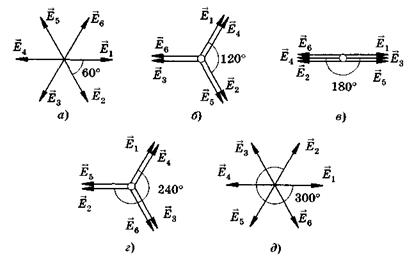
Рис. 19.14

.

Особо отметим роль минимумов от одной щели. В направле­нии, отвечающем условию (19.27), каждая щель дает минимум, поэтому минимум от одной щели сохранится и для всей решетки. Если для некоторого направления одновременно выполняются ус­ловия минимума для щели (19.27) и главного максимума решет­ки (19.29), то соответствующий главный максимум не возникнет. Обычно стараются использовать главные максимумы, которые размещаются между первыми минимумами от одной щели, т. е. в интервале

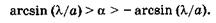(19.33)

При падении на дифракционную решетку белого или иного немо­нохроматического света каждый главный максимум, кроме цент­рального, окажется разложенным в спектр [см. (19.29)]. В этом случае k указывает порядок спектра.

Таким образом, решетка является спектральным прибором, поэтому для нее существенны характеристики, которые позволя­ют оценивать возможность различения (разрешения) спектраль­ных линий.

Одна из таких характеристик — угловая дисперсия — опреде­ляет угловую ширину спектра. Она численно равна угловому рас-

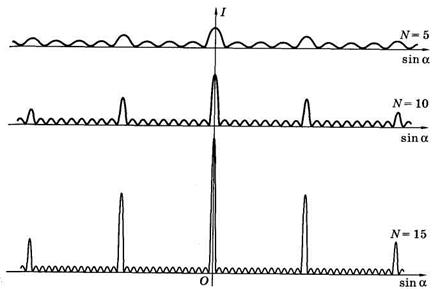
Рис. 19.16

стоянию da между двумя линиями спектра, длины волн которых различаются на единицу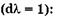

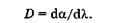
Дифференцируя (19.29) и используя только положительные значения величин, получаем

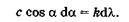
Из последних двух равенств имеем

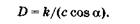(19.34)

Так как обычно используют небольшие углы дифракции, то

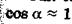. Угловая дисперсия D тем выше, чем больше порядок 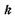спектра и чем меньше постоянная с дифракционной решетки.

Возможность различать близкие спектральные линии зависит не 1?олько от ширины спектра, или угловой дисперсии, но и от ширины Спектральных линий, которые могут накладываться друг на друга.

Принято считать, что если между двумя дифракционными мак­симумами одинаковой интенсивности находится область, где сум­марная интенсивность составляет 80% от максимальной, то спект­ральные линии, которым соответствуют эти максимумы, уже раз­решаются. При этом, согласно Дж. У. Рэлею, максимум одной линии совпадает с ближайшим минимумом другой, что и считает ся критерием разрешения. На рис. 19.17 изо­бражены зависимости интенсивности / отдель­ных линий от длины волны (сплошная кривая) и их суммарная интенсивность (штриховая кривая). Из рисунков легко увидеть неразре-шенность двух линий (а) и предельную разре-шенность (б), когда максимум одной линии совпадает с ближайшим минимумом другой.

Разрешение спектральных линий количе­ственно оценивается разрешающей способ­ностью, равной отношению длины волны к наименьшему интервалу длин волн, которые еще могут быть разрешены:

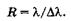(19.35)

Так, если имеются две близкие линии с длинами волн 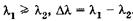, то (19.35) можно приближенно записать в виде

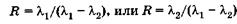. (19.36)

Условие главного максимума для первой волны

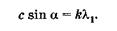
С ним совпадает ближайший минимум для второй волны, усло­вие которого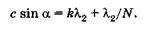

Приравнивая правые части последних двух равенств, имеем

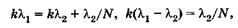
откуда [с учетом (19.36)]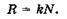

Итак, разрешающая способность дифракционной решетки тем больше, чем больше порядок 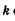спектра и число N штрихов.

Рассмотрим пример. В спектре, полученном от дифракционной ре­шетки с числом щелей N = 10 000, имеются две линии вблизи длины вол­ны 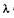= 600 нм. При какой наименьшей разности длин волн 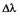эти линии различаются в спектре третьего порядка (k = 3)?

Для ответа на этот вопрос приравняем (19.35) и (19.37), 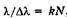,Откуда 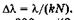Подставляя числовые значения в эту формулу, находим 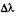= 600 нм(3* 10 000) = 0,02 нм.

Так, например, различимы в спектре линии с длинами волн 600,00 и 600,02 нм и не различимы линии с длинами волн 600,00 и 600,01 нм.

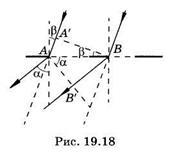
Выведем формулу дифракционной ре­шетки для наклонного падения когерент­ных лучей (рис. 19.18, 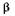— угол падения). Условия формирования дифракционной картины (линза, экран в фокальной плос­кости) те же, что и при нормальном паде­нии.

Проведем перпендикуляры А'В к падаю­щим лучам и АВ' ко вторичным волнам, идущим под углом 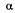к перпендикуляру, восставленному к плоскости решетки. Из рис. 19.18 видно, что к положению А'В лучи имеют одинаковую фазу, от АВ' и далее разность фаз лучей сохраняется. Следовательно, разность хо­да есть

d= ВВ'-АА. (19.38)

Из DАА'В имеем АА' = АВ sin (3 = с sin р. Из DВВ'А находим ВВ' = АВ sin a = = с sin а. Подставляя выражения для АА' и ВВ' в (19.38) и учитывая ус­ловие для главных максимумов, имеем

с (sin а - sin Р) = + kX. (19.39)

Центральный главный максимум соответствует направлению падающих лучей (а = b).

Наряду с прозрачными дифракционными решетками исполь­зуют отражательные, у которых штрихи нанесены на металличе­скую поверхность. Наблюдение при этом ведется в отраженном свете. Отражательные дифракционные решетки, изготовленные на вогнутой поверхности, способны образовывать дифракцион­ную картину без линзы.

В современных дифракционных решетках максимальное чис­ло штрихов составляет более 2000 на 1 мм, а длина решетки более 300 мм, что дает значение N около миллиона.

 

^{______________________}

¹ Из формулы (19.29) видно, что максимальное значение 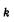не может превышать величины c/l.

 

 

§ 19.7. Основы рентгеноструктурного анализа

Основная формула дифракционной решетки (19.29) может быть использована не только для определения длины волны, но и для решения обратной задачи — нахождения постоянной дифрак­ционной решетки по известной длине волны. Такая скромная применительно к обычной дифракционной решетке задача подво­дит к практически важному вопросу — измерению параметров кристаллической решетки посредством дифракции рентгенов­ских лучей, что является содержанием рентгеноструктурного анализа.

CF — перпендикуляры к падающим и отраженным лучам соот­ветственно. Разность хода отраженных лучей 1’ и 2'

(19.41)

где t — межплоскостноерасстояние.

Максимумы интерференции при отражении возникают в слу­чае, когда разность хода равна целому числу длин волн:

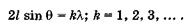(19.42)

Это условие Брэгга—Вульфа.

При падении монохроматического рентгеновского излучения на кристалл под разными углами наибольшее отражение (максимум) будет для углов, отвечающих условию (19.42). При регистрации под определенным углом скольжения пучка рентгеновского излу­чения со сплошным спектром максимум дифракции будет выпол­няться для длин волн, удовлетворяющих условию Брэгга—Вульфа.

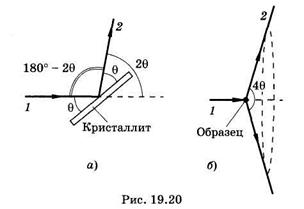
П. Дебаем и П. Шеррером был предложен метод рентгено-структурного анализа, основанный на дифракции монохромати­ческих рентгеновских лучей в поликристаллических телах (обыч­но спрессованные порошки). Среди множества кристаллитов всег­да найдутся такие, для которых одинаковы 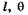и k, причем эти величины соответствуют формуле Брэгга—Вульфа. Отраженный луч 2 (максимум) составит угол 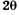с падающим рентгеновским лу­чом 1 (рис. 19.20, а). Так как условие (19.42) одинаково для мно­гих кристаллов, по-разному ориентированных, то дифрагирован­ные рентгеновские лучи образуют в пространстве конус, вершина которого лежит в исследуемом образце, а угол раствора равен 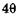(рис. 19.20, б). Другой совокупности величии 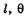и k, удовлетво­ряющих условию (19.42), будет соответствовать другой конус. На фотопленке рентгеновские лучи образуют рентгенограмму (дебае-грамму) в виде окружностей или дуг (рис. 19.21 а, б).

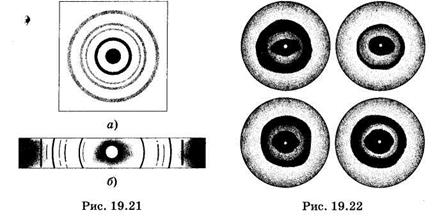
Дифракцию рентгеновских лучей наблюдают также при рассея­нии их аморфными твердыми телами, жидкостями и газами. В этом случае на рентгенограмме получаются широкие и размытые кольца.

В настоящее время широко применяют рентгеноструктурный анализ биологических молекул и систем: на рис. 19.22 показаны рентгенограммы белков. Этим методом Дж. Уотсон и Ф. Крик ус­тановили структуру ДНК и были удостоены Нобелевской премии (1962). Использование дифракции рентгеновских лучей от крис­таллов для исследования их спектрального состава относится к области рентгеновской спектроскопии.

 

§ 19.8. Понятие о голографии и ее возможном применении в медицине

Голография¹ — метод записи и восстановления волнового поля, основанный на интерференции и дифракции волн.

Идея голографии была впервые высказана Д. Габором в 1948 г., однако ее практическое использование оказалось возможным пос­ле появления лазеров.

Изложение основ голографии уместно начать сравнением с фо­тографией. При фотографировании на фотопленке фиксируется интенсивность световых волн, отраженных предметом. Изображе­ние в этом случае является совокупностью темных и светлых точек. Фазы рассеиваемых волн не регистрируются, и таким обра­зом пропадает значительная часть информации о предмете.

Голография позволяет регистрировать и воспроизводить более полную информацию об объекте с учетом амплитуд и фаз волн, рассеянных предметом. Регистрация фазы возможна вследствие интерференции волн. С этой целью на светофиксирующую по­верхность посылают две когерентные волны: опорную, идущую непосредственно от источника света или зеркал, которые исполь­зуют как вспомогательные устройства, и сигнальную, которая по­является при рассеянии (отражении) части опорной волны пред­метом и содержит соответствующую информацию о нем.

Интерференционную картину, образованную сложением сигнальной и опорной волн и зафиксированную на светочувст­вительной пластинке, называют голограммой. Для восстанов­ления изображения голограмму освещают той же опорной волной.

Покажем на некоторых примерах, как получается голограмма и восстанавливается изображение.

Голограмма плоской волны.В этом случае на голограмме фик­сируется плоская сигнальная волна /, попадающая под углом а_х на фотопластинку Ф (рис. 19.23, а).

Опорная волна // падает нормально, поэтому во всех точках фото­пластинки одновременно ее фаза одинакова. Фазы сигнальной волны вследствие ее наклонного падения различны в разных точках светочувствительного слоя. Из этого следует, что разность фаз между лучами опорной и сигналь­ной волн зависит от места встречи этих лучей на фотопластинке и, согласно условиям макси­мумов и минимумов интерференции, получен­ная голограмма будет состоять из темных и светлых полос.

Пусть АВ (рис. 19.23, б) соответствует рас­стоянию между центрами ближайших тем­ных или светлых интерференционных полос. > Это означает, что фазы точек А и В в сигналь­ной волне отличаются на 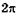. Построим нор-i маль АС к ее лучам (фронт волны). Очевидно, что фазы точек А и С одинаковы. Различие

фаз точек В и С на 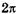означает, что 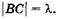Из прямоугольного 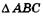имеем

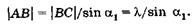(19.43)

Итак, в этом примере голограмма подобна дифракционной решетке, так как на светочувствительной поверхности зарегистрированы.

 

Направив на голограмму опорную волну II (рис. 19.24), осуществим дифракцию (см. § 19.6). Соглас­но (19.29), первые главные максимумы (k = 1) соответствуют на­правлениям

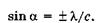(19.44)

Подставив в это выражение АВ из (19.43) вместо с, имеем

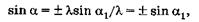(19.45)

откуда

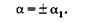(19.46)

Из (19.46) видно, что направление волны I’ (рис. 19.24), дифра­гированной под углом 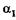, соответствует сигнальной: так восстанав­ливают волну, отраженную (рассеянную) предметом. Волна I" и вол­ны остальных главных максимумов (на рисунке не показаны) также воспроизводят информацию, зафиксированную в голограмме.

Голограмма точки.Одна часть опорной волны II попада­ет на точечный объект А (рис. 19.25, а) и рассеивается от него

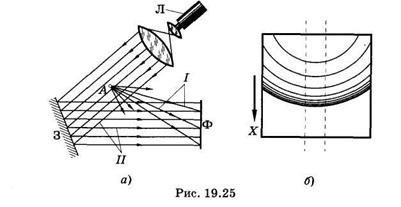
в виде сферической сигнальной волны /, другая часть плос­ким зеркалом 3 направляется на фотопластинку Ф, где эти вол­ны и интерферируют. Источником излучения является лазер Л. На рис. 19.25, б схематически изображена полученная голо­грамма.

Хотя в данном примере сигнальная волна является сфериче­ской, можно с некоторым приближением применить формулу (19.43) и заметить, что по мере увеличения угла а₁ (см. рис. 19.23, а) уменьшается расстояние АВ между соседними полосами. Нижние дуги на голограмме (рис. 19.25, б) расположены более тесно.

Если вырезать из голограммы узкую полоску, показанную штриховыми линиями на рис. 19.25, б, то она будет подобна уз­кой дифракционной решетке, постоянная которой уменьшается в направлении оси X. На такой решетке отклонение вторичных волн, соответствующих первому главному максимуму, возрастает по мере увеличения координаты X щели [см. (19.29)]: с становит­ся меньше, |sin a| — больше.

Таким образом, при восстановлении изображения плоской опорной волной дифрагированные волны уже не будут плоскими. На рис. 19.26 показаны волна /', формирующая мнимое изобра­жение А' точки А, и волна I", создающая действительное изобра­жение А".

Так как рассеянные предметом волны попадают совместно с опорной волной во все точки голограммы, то все ее участки содер­жат информацию о предмете, и для восстановления изображения не обязательно использовать полностью всю голограмму. Следу­ет, однако, заметить, что качество восстановленного изображения тем хуже, чем меньшую часть голограммы для этого применяют. Из рис. 19.26 видно, что мнимое и действительное изображения образуются и в том случае, если восстановление осуществляют,

например, нижней половиной го­лограммы, однако изображение при этом формируется меньшим коли­чеством лучей.

Любой предмет является сово­купностью точек, поэтому рассуж­дения, приведенные для одной точ­ки, могут быть обобщены и на го­лографирование любого предмета. Голографические изображения объ­емны, и их зрительное восприятие ничем не отличается от восприятия

соответствующих предметов²: ясное видение разных точек изображения осуществляется посредством аккомодации глаза (см. § 21.4); при изменении точки зрения изменяется перспектива, одни детали изображения могут заслонять другие.

При восстановлении изображения можно изменить длину опорной волны. Так, например, голограмму, образованную неви­димыми электромагнитными волнами (ультрафиолетовыми, инф­ракрасными и рентгеновскими), можно восстановить видимым светом. Так как условия отражения и поглощения электромаг­нитных волн телами зависят, в частности, от длины волны, то эта особенность голографии позволяет использовать ее как метод внутривидения, или интроскопии³.

Особо интересные и важные перспективы открываются в связи с ультразвуковой голографией. Получив голограмму в ультразву­ковых механических волнах, можно восстановить ее видимым све­том. Ультразвуковая голография в перспективе может быть ис­пользована в медицине для рассматривания внутренних органов человека с диагностической целью. Учитывая большую информа­тивность этого метода и существенно меньший вред ультразвука по сравнению с рентгеновским излучением, можно ожидать, что в будущем ультразвуковая голографическая интроскопия заменит традиционную рентгенодиагностику.

Еще одно медико-биологическое приложение голографии свя­зано с голографическим микроскопом. Один из первых способов построения голографического микроскопа основан на том, что изображение предмета получается увеличенным, если голограм­му, записанную с плоской опорной волной, осветить расходящей­ся сферической волной.

В развитие голографии внес вклад советский физик Ю. Н. Де-нисюк, разработавший метод цветной голографии.

Сейчас трудно оценить все возможности применения гологра­фии: кино, телевидение, запоминающие устройства и т. д. Несом­ненно лишь, что голография является одним из величайших изо­бретений XX в.

 

¹ Голография (греч.) — полная запись.

² Некоторое отличие обусловлено одноцветностью изображения, ко­торое неизбежно при записи и восстановлении монохроматической вол­ной.

³ Intro (лат.) — внутри и skopeo (лат.) — смотрю. Ризуальное наблюдение объектов, явлений и процессов в оптически непрозрачных телах и средах, а также в условиях плохой видимости

.

 

ГЛАВА 20