Геометрическая оптика

Геометрическая (лучевая) оптика — раздел, в котором изучав ют законы распространения света на основании представле­ния о световом луче как линии, вдоль которой распространя­ется энергия световой волны.

В главе законы геометрической оптики применяются к рас­смотрению конкретных оптических систем. Наряду с этим излагаются также вопросы физики глаза.

§ 21.1. Геометрическая оптика как предельный случай волновой оптики

В предыдущих главах были рассмотрены явления, для описа­ния которых необходимо учитывать волновую природу света. Од­нако во многих практических вопросах, таких, как формирова­ние светового пучка, образование изображения и др., волновые свойства света могут оказаться несущественными. Более того, учет интерференции, дифракции и поляризации в этих случаях лишь усложнит получение конечного результата. Для решения такого рода задач применяют законы геометрической оптики.

Геометрическая оптика есть предельный случай волновой оп­тики при стремлении длины волны к нулю. Это можно пояс­нить на примере дифракционной решетки. Из (19.26) при 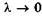следует 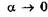, т. е. получаем обычное для линзы фокусирование параллельного пучка света в точке О фокальной плоскости (см. рис. 19.10).

Для выяснения предельных возможностей оптических систем вновь приходится учитывать волновой характер света. Поэтому в этой главе частично рассматриваются вопросы интерференции и дифракции.

Геометрическая оптика является примером теории, позволив­шей при небольшом числе основных понятий и законов получить много практически важных результатов. В теории оптических устройств она и сейчас имеет большое значение.

§ 21.2. Аберрации линз

Приведем формулу тонкой линзы, известную из школьного курса:

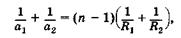(21.1)

где а₁ — расстояние от предмета до линзы, а₂ — расстояние от изо­бражения до линзы, Ry и R₂ — радиусы кривизны передней и за­дней сферических поверхностей линзы соответственно, п — показа­тель преломления вещества, из которого изготовлена линза; окру­жающая среда — воздух. Фокусное расстояние для такой линзы

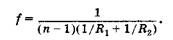(21.2)

Учитывая (21.2), формулу тонкой линзы представим в виде

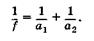(21.3)

Соотношение (21.1) полученодля тонкой линзы при следую­щих предположениях: 1) изображение формируется узкими приосевыми (параксиальными) пучками, составляющими неболь­шие углы с главной осью системы; 2) показатель преломления для всех длин волн одинаков. При выполнении таких условий со­здается точечное изображение, т. е. каждая точка предмета дает одну точку изображения.

Эти условия не реализуются на практике. Показатель прелом­ления зависит от длины волны (дисперсия). Точки предмета ле­жат в стороне от оптической оси, что не отвечает первому усло­вию. Применение только параксиальных лучей существенно ог­раничило бы световые потоки.

Все это приводит к аберрациям¹, или погрешностям, реальных оптических систем, существенно снижающим качество оптических изображений. Однако, зная причины аберраций, можно добиться их устранения, если соответствующим образом подобрать систему линз.

Рассмотрим некоторые основные аберрации линзы.

Сферическая аберрация.Она заключается в том, что пери­ферические части линзы сильнее отклоняют лучи, идущие от точ­ки S на оси, чем центральные (рис. 21.1). Вследствие этого изображение светящейся точки на экране Э имеет вид светлого пят­на. Для устранения сферической аберрации создают систему из вогнутой и выпуклой линз.

Астигматизм². Это недостаток оптической системы, при кото­ром сферическая световая волна, проходя оптическую систему, деформируется и перестает быть сферической.

Различают два вида астигматизма. Один из них обусловлен па­дением на оптическую систему лучей, составляющих значитель­ный угол с оптической осью (астигматизм косых пучков).

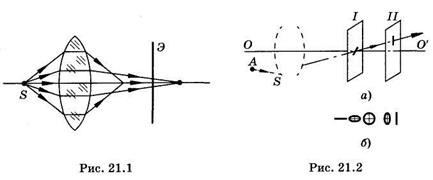
Пусть точка А предмета расположена вне главной оптической оси (рис. 21.2, а); из всех лучей, идущих от этой точки, выделим небольшой элементарный пучок таким образом, чтобы его цент­ральный луч AS лежал в одной плоскости с главной оптической осью ОО'. Любую плоскость, проходящую через главную оптиче­скую ось, называют меридиональной; в данном примере возьмем плоскость, в которой лежат центральный луч элементарного пуч­ка и главная оптическая ось (на рис. 21.2, а — плоскость чер­тежа).

При наклонном падении элементарного пучка линза создаст два изображения точки А в виде отрезков прямой. Один из них лежит в меридиональной плоскости и отчетливо виден на экране II (см. рис. 21.2, а), другой — в перпендикулярной плоскости, которую называют сагиттальной, он отчетливо виден на экране I. В про­межутке между плоскостями I и II наблюдается пятно рассеяния, имеющее форму эллипса или окружности (рис. 21.2, б). Если пред­метом является отрезок линии, то качество изображения зависит от ориентации отрезка. Отрезки, расположенные в меридиональ­ных плоскостях³, дают четкое изображение в плоскости II, а рас­положенные в сагиттальных плоскостях — в плоскости I.

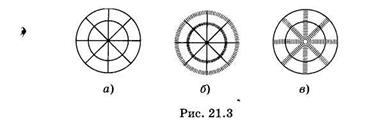
Для демонстрации астигматизма косых пучков удобна сетка, представленная на рис. 21.3, а. Помещая ее как предмет перпен­дикулярно оптической оси, зададим систему отрезков, лежащих в меридиональных плоскостях (радиусы) и сагиттальных (окруж­ности). На рис. 21.3, б, в показаны изображения этих отрезков, полученные в соответствующих плоскостях.

Для исправления астигматизма создают сложные оптические системы, состоящие из нескольких линз, благодаря чему удается об­разовать хорошие изображения при углах падения лучей 50—70°.

Другой вид астигматизма обусловлен асимметрией оптиче­ской системы. Линзы с такой аберрацией называют астигмати­ческими. Эти линзы, как и в случае астигматизма косых пучков, создают изображение, в котором контуры и линии, ориентирован­ные в разных направлениях, имеют разную резкость.

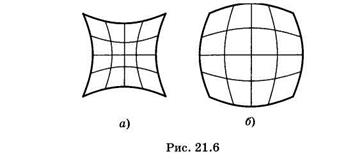
Дисторсия.Этот вид аберрации возникает вследствие того, что лучи, посылаемые предметом в систему, составляют большие углы с оптической осью, при этом зависимость линейного увели­чения от угла пучка приводит к нарушению подобия изображе­ния и предмета. Типичные проявления дисторсии показаны на рис. 21.6: а — подушкообразная; б — бочкообразная; предметом является сетка с квадратными ячейками.

Подбирая систему из нескольких линз с противоположным ха­рактером дисторсии, можно исправить эту аберрацию.

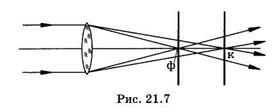
Хроматическая аберрация.Как видно из (21.2), фокусное расстояние линзы определяется показателем преломления, кото­рый зависит от длины волны. Поэтому пучок белого света, идущий параллельно главной оптической оси, будет фокусироваться в раз­ных ее точках, разлагаясь в спектр (рис. 21.7; ф — фиолетовые лучи, к — красные), кружок на экране окажется окрашенным. В этом заключается хроматическая аберрация, которая очень час­то сопутствует изображениям в линзах.

Для исправления этого вида аберрации создают ахроматиче­ские оптические системы из линз, которые изготовляют из стекол с разной дисперсией: ахроматы и апохроматы.

В оптических устройствах используют системы из линз, назы­ваемые анастигматами, в которых исправлены не только хро­матическая аберрация, но и сферическая, а также и астигматизм.

Существуют и другие виды аберраций, которые здесь не рас­сматриваются .

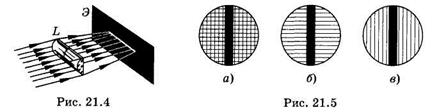
Наиболее наглядно астигматизм такого типа можно продемонст­рировать на цилиндрической линзе (рис. 21.4). Пучок лучей, па­раллельных главной оптической оси, преломляется линзой L только в плоскостях, перпендикулярных образующей цилиндра, поэтому на экране Э, расположенном в фокальной плоскости линзы, наблю­дается прямая линия, а не точка, как при сферических линзах. Ес­ли с помощью цилиндрической линзы отобразить на экране сетку из тонкой проволоки с квадратными ячейками (рис. 21.5, а), то наибо­лее четкое изображение получается в виде системы параллельных линий, направленных вдоль образующей цилиндра (рис. 21.5, б, в; изображения соответствуют двум взаимно перпендикулярным поло­жениям цилиндрической линзы).

Одновременное устранение всех аберраций может оказаться слишком слояшой или даже неразрешимой задачей, поэтому обычно избавляют­ся только от тех погрешностей, которые существенно мешают основному назначению оптической системы. Так, для объективов микроскопов важ­но устранение сферической аберрации, возникающей при рассматрива­нии объектов, лежащих вблизи фокуса и отображаемых широкими пуч­ками.

¹ Aberratio (лат.) — уклонение.

² Астигматизм — не точечный. Точке предмета соответствует не одна точка изображения.

³Предполагается, что предмет лежит в плоскости, перпендикуляр­ной главной оптической оси.

§ 21.3. Понятие об идеальной центрированной оптической системе

Реальные оптические системы состоят из различных деталей и часто включают в себя несколько линз (см. § 21.2). При произ­вольном расположении линз расчет и построение изображений могут быть достаточно сложными.

На практике часто используют системы сферических поверх­ностей (линз), центры которых лежат на одной прямой — главной оптической оси. Такие оптические системы называют центриро­ванными.

Рассмотрим некоторые выводы теории идеальных центриро­ванных оптических систем, предложенной Гауссом. В таких системах каждой точке или линии пространства предметов соот­ветствует только одна точка или линия пространства изображе­ний. Соответственные пары точек или линий обоих пространств называют сопряженными. К идеальной центрированной оптиче­ской системе приближаются такие, в которых используются па­раксиальные лучи. Такая система есть физическая абстракция, позволяющая рассчитывать реальные системы с учетом степени их отклонения от идеальной.

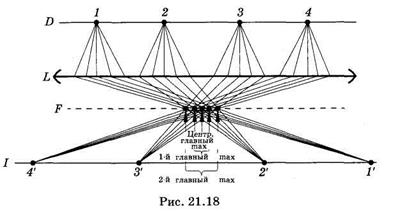
Укажем характерные точки и плоскости центрированной оп­тической системы (рис. 21,8; Q₁ и Q₂ — крайние сферические по­верхности), принятые в теории Гаусса, с помощью которых мож­но построить изображения предметов.

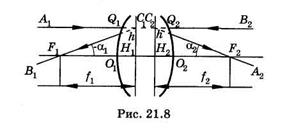
Проведем в пространстве предметов луч A1 параллельный главной оптической оси О1О₂. В пространстве изображений ему сопряжен луч А₂, проходящий через точку F₂. Точка F₂ простран­ства изображений, сопряженная бесконечно удаленной точке про­странства предметов, является вторым, или задним, фокусом системы.

Аналогично, лучу В₂ пространства изображений соответствует

луч В₁ пространства предметов, проходящий через точку F1 Точ­ка .F1 пространства предметов, сопряженная бесконечно удален­ной точке пространства изображений, является первым, или пе­редним, фокусом¹.

Плоскости, проходящие через фокусы перпендикулярно глав­ной оптической оси, называют фокальными.

Так как лучи А₁ и В1 попарно сопряжены лучам А₂ и В₂, то со­пряжены и точки C1 и С₂ пересечения этих лучей или их продол­жений. Проведя через С1 и С₂ плоскости, перпендикулярные О1О₂, получим точки Ну и Н₂. Имеем попарное сопряжение этих плоскостей, точек Н1 и Н₂ и отрезков С1Н1 и С₂Н₂.

Отрезки С₁Н₁ и С₂Н₂ не только сопряжены, но и равны (IC^ffJ = = |С₂Д"₂| = h) и имеют одинаковое направление относительно опти­ческой оси (одинаковые знаки); следовательно, для них линейное увеличение р* = +1. Оптическая система имеет две сопряженные плоскости, перпендикулярные оптической оси, для которых ли­нейное увеличение сопряженных отрезков b = +1; такие плоскос­ти и соответствующие точки Н₁ и Н₂ главной оптической оси на­зывают главными.

Расстояния между фокусами и соответствующими главными точками называют фокусными расстояниями:

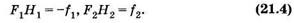
Главные плоскости и точки Н1 и Н₂ мо­гут лежать не только внутри центрирован­ной оптической системы (см. рис. 21.8), но и вне ее, совершенно не симметрично относи­тельно граничных поверхностей (рис. 21.9).

Главные точки и фокусы называют кар­динальными точками, а соответствующие плоскости — кардинальными плоскостями. Эти точки и плоскости используют для построения изображения безотносительно к ис­тинному ходу лучей в системе. Общие принципы аналогичны пра­вилам построения изображения в тонкой линзе.

На рис. 21.10 показан пример построения изображения в цент­рированной оптической системе. Луч 1, идущий от светящейся точки S_l параллельно главной оптической оси, продолжают до пе­ресечения с главной плоскостью пространства изображений, а за­тем проводят через фокус F₂. Луч 2 проходит через фокус F1до пе­ресечения с главной плоскостью пространства предметов, а затем параллельно оптической оси. Пересечение двух лучей (точка <S₂) ^и дает изображение точки S1

Точки N₁ и N₂ (см. рис. 21.10) называют узловыми. Их особен­ность заключается в том, что сопряженные лучи 3, проходящие через них, одинаково наклонены к оптической оси, т. е. параллельны.

Если по обе стороны от оптической системы находятся среды с одинаковыми показателями преломления, то узловые точки сов­падают с соответствующими главными точками.

Таким образом, оптическая система характеризуется шестью кардинальными точками и шестью кардинальными плоскостями.

Приведем без вывода наиболее важные формулы для центриро­ванной оптической системы:

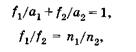(21.5) (21.6)

где n1 и п₂ — показатели преломления сред соответственно слева и справа от крайних сферических поверхностей оптической систе­мы; обозначения a1 a₂, f_v f₂ разъяснены на рис. 21.10. Отрезки а_х и f_x отсчитываются от главной точки H1а отрезки a_{2 и} f₂ — от Н₂.

Они считаются положительными, если их направления совпада­ют с направлением распространения света, и отрицательными, ес­ли они противоположны. Обычно в геометрической оптике на ри­сунках принято распространение света слева направо.

Так как тонкая линза является частным случаем центрирован­ной оптической системы, то естественно, что все сказанное выше справедливо и для нее. В этом случае четыре кардинальные точки — главные и узловые — совпадают с центром линзы, а фор­мула (21.5) превращается в (21.3). Правила построения изображе­ния в таких линзах, известные читателю из средней школы, также являются частным случаем более общего метода, описанного выше.

¹ Так как пространства предметов и изображений взаимно сопряже­ны, то понятия «передний» и «задний», «первый» и «второй» условны.

§ 21.4. Оптическая система глаза и некоторые ее особенности

Глаз человека является своеобразным оптическим прибором, занимающим в оптике особое место. Это объясняется, во-первых, тем, что многие оптические инструменты рассчитаны на зритель­ное восприятие, во-вторых, глаз человека (и животного) как усо­вершенствованная в процессе эволюции биологическая система приносит в рамках бионики некоторые идеи по конструированию и улучшению оптических систем.

Для медиков глаз не только орган, способный к функциональ­ным нарушениям и заболеваниям, но и источник информации о некоторых неглазных болезнях.

Остановимся кратко на строении глаза человека.

Собственно глазом (рис. 21.11) является глазное яблоко, имею­щее не совсем правильную шаровидную форму: передне-задний размер у взрослого в среднем 24,3 мм, вертикальный — 23,4 мм и горизонтальный — 23,6 мм. Стенки глаза состоят из трех концент рически расположенных оболочек: на­ружной, средней и внутренней. Наруж­ная белковая оболочка — склера 1 — в передней части глаза превращается в прозрачную выпуклую роговую оболоч­ку 2 — роговицу. Толщина роговицы в центре около 0,6 мм, на периферии — до 1 мм. По оптическим свойствам рого­вица — наиболее сильно преломляю­щая часть глаза. Она является как бы окном, через которое в глаз проходят лучи света. Радиус кривизны роговицы примерно 7—8 мм, показатель преломления ее вещества 1,38. На­ружный покров роговицы переходит в конъюнктиву 3, прикреплен­ную к векам.

К склере прилегает сосудистая оболочка 4, внутренняя поверх­ность которой выстлана слоем темных пигментных клеток, препят­ствующих внутреннему диффузному рассеянию света в глазу. В пе­редней части глаза сосудистая оболочка переходит в радужную 5, в которой имеется круглое отверстие — зрачок 6. Непосредственно к зрачку с внутренней стороны глаза примыкает хрусталик 7 — проз­рачное и упругое тело, подобное двояковыпуклой линзе. Диаметр хрусталика 8—10 мм, радиус кривизны передней поверхности в среднем 10 мм, задней — 6 мм. Показатель преломления вещества хрусталика несколько превышает значение п = 1,4^х.

Между роговицей и хрусталиком расположена передняя каме­ра 8 глаза, она заполнена водянистой влагой — жидкостью, близ­кой по оптическим свойствам к воде. Вся внутренняя часть глаза от хрусталика до задней стенки занята прозрачной студенистой массой, называемой стекловидным телом 9. Показатель прелом­ления стекловидного тела такой же, как и у водянистой влаги.

Рассмотренные выше элементы глаза в основном относятся к его светопроводящему аппарату.

Зрительный нерв 10 входит в глазное яблоко через заднюю стенку; разветвляясь, он переходит в самый внутренний слой гла­за — сетчатку, или ретину 11, являющуюся световоспринимающим (рецепторным) аппаратом глаза. Сетчатка состоит из не­скольких слоев и неодинакова по своей толщине и чувствитель­ности к свету, в ней находятся светочувствительные зрительные клетки, периферические концы которых имеют различную фор­му. Продолговатые окончания называют палочками, конусооб­разные — колбочками. Длина палочек 63—81 мкм, диаметр око­ло 1,8 мкм, для колбочек, соответственно, 35 и 5—6 мкм. На сет­чатке глаза человека расположено около 130 млн палочек и 7 млн колбочек.

В месте вхождения зрительного нерва находится не чувстви­тельное к свету слепое пятно 12. В середине сетчатки, чуть ближе к височной области, лежит самое чувствительное к свету желтое пятно 13, центральная часть которого имеет диаметр около 0,4 мм»

Колбочки и палочки распределены по сетчатке неравномерно. Колбочки расположены главным образом в центральной части сетчатки, в желтом пятне, в центре желтого пятна находятся иск­лючительно колбочки, на краях сетчатки — только палочки.

Рассмотрим сначала особенности светопроводящего аппарата глаза.

Глаз может быть представлен как центрированная оптическая система, образованная роговицей, жидкостью передней камеры и хрусталиком (четыре преломляющие поверхности) и ограничен­ная спереди воздушной средой, сзади — стекловидным телом. Главная оптическая ось ОО (см. рис. 21.11) проходит через гео­метрические центры роговицы, зрачка и хрусталика. Кроме того, различают еще зрительную ось О'О' глаза, которая определяет на­правление наибольшей светочувствительности и проходит через центры хрусталика и желтого пятна. Угол между главной оптиче­ской и зрительной осями составляет около 5°.

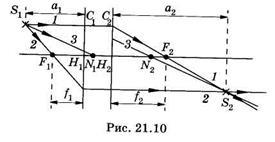
На рис. 21.12 показаны фокусы, главные точки и плоскости, а также узловые точки для некоторого усредненного нормального глаза (расстояния указаны в миллиметрах). Для упрощения час­то заменяют эту систему приведенным редуцированным глазом, т. е. линзой, окруженной воздухом со стороны пространства пред­метов и жидкостью с показателем преломления п = 1,336 со сто­роны пространства изображений. В одной из моделей приведен­ного глаза единая главная плоскость находится на расстоянии 1,6 мм от передней поверхности роговицы, узловые точки совпада­ют и расположены на расстоянии 7,2 мм от поверхности роговицы.

Основное преломление света происходит на внешней границе роговицы, оптическая сила всей роговицы равна приблизитель­но 40 дптр, хрусталика — около 20 дптр, а всего глаза — около 60 дптр.

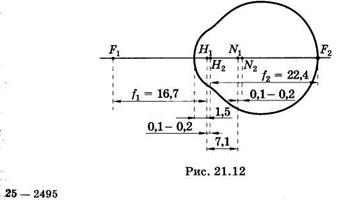
Различно удаленные предметы должны давать на сетчатке оди­наково резкие изображения. Из формулы (21.5) видно, что это мож­но осуществить либо изменяя расстояние а₂ между главной плоско­стью и сетчаткой аналогично тому, как это делают в фотоаппаратах, либо изменяя кривизну хрусталика и, следовательно, фокусные рас­стояния f1и f₂. В глазу человека реализуется второй случай.

Приспособление глаза к четкому видению различно удаленных предметов — «наводку на резкость» — называют аккомодацией¹.

Когда предмет расположен в бесконечности, то его изображение в нормальном глазу находится на сетчатке. Хрусталик при этом акко­модирован на бесконечность и его оптическая сила наименьшая. Ес­ли предмет приближается к глазу, то у хрусталика увеличивается кривизна; чем ближе предмет, тем больше оптическая сила глаза, ее изменения происходят приблизительно в пределах 60—70 дптр.

У взрослого здорового человека при приближении предмета к глазу до расстояния 25 см аккомодация совершается без напряже­ния и благодаря привычке рассматривать предметы, находящие­ся в руках, глаз чаще всего аккомодирован именно на это расстоя­ние, называемое расстоянием наилучшего зрения.

Для рассматривания еще более близких предметов приходится уже напрягать аккомодационный аппарат. Наиболее близкое распо­ложение предмета от глаза, при котором еще возможно четкое изо­бражение на сетчатке, называют ближней точкой глаза (ближняя точка ясного видения). Расстояние до ближней точки глаза с возрас­том увеличивается; следовательно, аккомодация уменьшается.

Размер изображения на сетчатке зависит не только от размера предмета, но и от его удаления от глаза, т. е. от угла, под которым виден предмет. В связи с этим вводят понятие угла зрения. Это угол между лучами, идущими от крайних точек предмета через совпадающие узловые точки (рис. 21.13). Из рисунка видно,

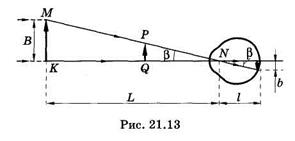
во-первых, что один и тот же угол зрения 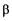может соответствовать разным предметам КМ и QP и, во-вторых, что угол зрения вполне определяет размер изображения на сетчатке:

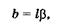(21.7)

где I — расстояние между единой узловой точкой N и сетчаткой (I ~ 17 мм). Формула (21.7) записана в предположении, что угол зрения мал.

Из рис. 21.13 легко установить связь между размером В пред­мета, расстоянием L его от глаза, точнее, от узловых точек, и уг­лом зрения :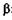

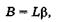(21.8)

отсюда с учетом (21.7) имеем

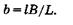(21.9)

Для характеристики разрешающей способности глаза исполь­зуют наименьший угол зрения, при котором человеческий глаз еще различает две точки предмета. Этот угол приблизительно ра­вен 1', что соответствует [см. (21.8)] расстоянию между точками, равному 70 мкм, если они находятся на расстоянии наилучшего зрения. Размер изображения на сетчатке в этом случае [см. (21.7)] равен 5 мкм, что соответствует среднему расстоянию между дву­мя колбочками на сетчатке. Поэтому если изображение двух то­чек на сетчатке займет линию короче 5 мкм, то эти точки не раз­решатся, т. е. глаз их не различает.

Такое же значение наименьшего угла зрения будет получено, если учесть ограничения, которые накладывает дифракция све­та (см. § 21.8). Поражает целесообразность природы — «ничего лишнего»: число колбочек, приходящихся на единицу площа­ди сетчатки, отвечает предельным возможностям геометрической оптики.

В медицине разрешающую способность глаза оценивают ост­ротой зрения. За норму остроты зрения принимается единица, в этом случае наименьший угол зрения равен 1'.

При отклонениях острота зрения во столько раз меньше нор­мы, во сколько раз наименьший угол зрения больше минуты. Если наименьший угол зрения равен 4', то острота зрения равна 1:4 = 0,25.

В отдельных случаях глаз человека различает и более мелкие величины, чем те, которые соответствуют углу 1'. Так, например, смещение движущихся предметов заметно, когда оно достигает 20" по дуге, несовпадение двух тонких линий обнаруживается уже при угле 12" между ними и т. д. В физических измерениях часто применяют приборы, в которых стрелка не должна смещаться с нулевого деления (штриха) шкалы (потенциометры, мосты). Благодаря способности глаза обнаруживать малые смеще­ния линий такие приборы могут давать более точные показания, чем те, в которых определяется расстояние между штрихом и стрелкой².

Чувствительность глаза к свету и цвету, а также биофизиче­ские вопросы зрения рассматриваются в седьмом разделе.

¹ Строение хрусталика напоминает слоистую структуру лука, Причем показатель преломления слоев неодинаков. Вследствие этой специфики хрусталик преломляет так, как однородное вещество с показателем пре­ломления, большим показателя преломления любого слоя.

² У некоторых рыб аккомодация происходит за счет перемещения хрусталика в целом относительно оптической оси, т. е. реализуется пер­вый случай.

 

 

§ 21.5. Недостатки оптической системы глаза и их компенсация

Аберрации, свойственные линзам, у глаз почти не ощущаются.

Сферическая аберрация незаметна ввиду малости зрачка и проявляется лишь в сумерках, когда зрачок расширен: изображе­ния нерезки. Хотя глаз и не является ахроматической системой, однако хроматическая аберрация не ощущается, в частности из-за малого размера зрачка. Астигматизм косых пучков не имеет места, так как глаз всегда устанавливается в направлении наблю­даемого предмета. Исключение составляет лишь астигматизм, обусловленный асимметрией оптической системы (несферическая форма роговицы или хрусталика).

Это проявляется, в частности, в неспособности глаза одинаково резко видеть взаимно перпендикулярные линии на испытатель­ной таблице. Такой недостаток глаза компенсируют специальны­ми очками с цилиндрическими линзами.

Оптической системе глаза свойственны некоторые специфиче­ские недостатки.

В нормальном глазу при отсутствии аккомодации задний фо­кус совпадает с сетчаткой — такой глаз называют эмметропическим; глаз называют аметропическим, если это условие не вы­полняется.

Наиболее распространенными видами аметропии являются близорукость (миопия) и дальнозоркость (гиперметропия). Близорукость — недостаток глаза, состоящий в том, что задний фокус при отсутствии аккомодации лежит впереди сетчатки; в случае дальнозоркости задний фокус при отсутствии аккомода­ции лежит за сетчаткой. Для коррекции близорукого глаза при­меняют рассеивающую линзу, дальнозоркого — собирающую.

¹ Это вопрос не только физический, но и физиологический.

 

 

§ 21.6. Лупа

Возможность разрешения деталей предмета зависит от размеров его изображения на сетчатке глаза или от угла зрения. Угол зрения можно увеличить, приблизив предмет к глазу, однако это связано с некоторыми ограничениями: 1) в ряде случаев технически невоз­можно существенно изменить расстояние между предметом и гла­зом (например, при рассмотрении звезд или Солнца); 2) невозмож­но приблизить предмет на расстояние меньшее, чем до ближней точки глаза, из-за предельных возможностей аккомодации.

В связи с этим для увеличения угла зрения используют оптиче­ские приборы: телескопы, лупы, микроскопы и т. п.

Рассмотрим устройство одного из наиболее простых оптиче­ских приборов — лупы.

Лупой называют оптическую систему, в передней фокаль­ной плоскости которой или в непосредственной близости от нее расположен наблюдаемый предмет.

Изображение, создаваемое лупой, находится в бесконечности или на удобном для глаза расстоянии. Если изображение в беско­нечности, то оно наблюдается глазом без аккомодации.

На рис. 21.14, а показано двумя лучами, как с помощью лупы формируется изображение на сетчатке; N — объединенная узловая точка оптической системы глаза, предмет помещен в передней фо­кальной плоскости. Луч 1 проходит через центр лупы без преломле­ния, а затем преломляется глазом. Другие лучи, идущие от этой же

 

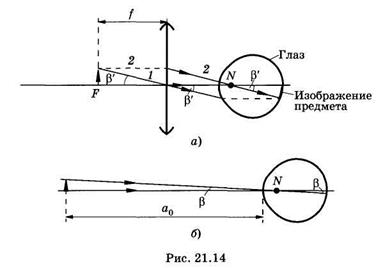
точки предмета, после преломления в лупе будут параллельны лучу 1. Чтобы определить положение изображения на сетчатке, выберем из этих лучей тот, который проходит через объединенную узловую точку (луч 2). Он не преломляется глазом. Его пересечение с сетчат­кой и укажет положение изображения предмета. Остается лишь для полноты картины достроить начальную часть луча 2 и конечную часть луча 1 (показаны штриховыми линиями).

Увеличением лупы называют отношение угла зрения 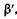под которым видно изображение предмета (см. рис. 21.14, а), к углу зрения 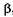, под которым виден предмет, находящийся на расстоя­нии наилучшего зрения а₀ = 25 см (рис. 21.14, б).

Из рисунков видно:

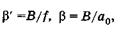(21.10)

где В — линейный размер предмета. Учитывая (21.10), получаем увеличение лупы

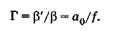(21.11)

Отсюда видно, что формула для увеличения связывает посто­янную величину фокусного расстояния f лупы с расстоянием на­илучшего зрения — довольно условной величиной. У близорукого глаза а₀ < 25 см, у дальнозоркого а₀ > 25 см, поэтому для близору­кого глаза увеличение от одной и той же лупы будет меньше, чем для дальнозоркого.

Учитывая, что напряжение аккомодации сильно утомляет глаз и допустимо лишь как кратковременное явление, следует при пользовании лупой помещать предмет в фокальную плоскость, а глаз — у самой лупы.

Лупы изготовляют из одной или нескольких линз. Увеличение лупы зависит от ее конструкции и изменяется в пределах от 2 до 40—50. Наиболее распространены лупы с 10-кратным увеличением.

Разрешаемое с помощью лупы расстояние между двумя точками мож­но вычислить по формуле (21.8). Например, если для 10-кратного увели­чения взять,

то получим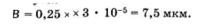

 

 

§ 21.7. Оптическая система и устройство микроскопа

Для получения больших увеличений в качестве лупы следует использовать [см. (21.11)]короткофокусные линзы. Однако такие линзы имеют небольшие размеры, им свойственны значительные

аберрации, что накладывает ограничения на увеличение лупы. Большее увеличение можно осуществить, рассматривая действи­тельное изображение предмета, созданное дополнительной лин­зой или системой линз. Таким оптическим устройством является микроскоп; лупу в этом случае называют окуляром, а дополни­тельную линзу или систему линз — объективом.

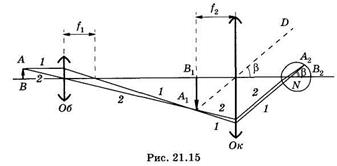
Для того чтобы глаз не был напряжен, стремятся совместить изображение, созданное объективом, с фокальной плоскостью окуляра. На рис. 21.15 показан ход лучей в микроскопе, объекти­вом и окуляром которого являются собирающие линзы, и в глазу.

Изображение А₁В₁ предмета АВ, созданное линзой объектива Об, находим согласно правилу построения изображения в тонкой линзе; луч 1, параллельный главной оптической оси, проходит после преломления в линзе через фокус, луч 2 через центр линзы идет без преломления; изображение А1В₁ расположено в передней фокальной плоскости окуляра.Лучи 1 и 2 доходят до линзы окуляра Ок и в ней преломляют­ся. Чтобы показать ход этих лучей после преломления в окуляре, проведем следующее рассуждение.

Все лучи, идущие из некоторой точки фокальной плоскости (например, A1, после преломления в линзе должны распростра­няться параллельно друг другу. Проведем из А₁ луч A1D через центр линзы; лучи 1 и 2 после преломления в окуляре пройдут па­раллельно A_tD до встречи с глазом. Пусть луч 1 проходит через объединенную узловую точку N глаза и потому без преломления дойдет до точки А₂ сетчатки. В эту же точку сфокусируется луч 2. На сетчатке глаза получаем изображение А₂В₂ предмета АВ.

В современных оптических микроскопах объектив и окуляр состоят из нескольких линз, представляющих собой единую

центрированную оптическую систему (рис. 21.16). Главные плоскости объектива и окуляра такой системы показаны на ри­сунке раздельно, окружающая среда имеет одинаковый показа­тель преломления. Лучи 1 и 2, идущие от точки В предмета АВ, пересекаются в точке В', где формируется изображение, создавае­мое объективом. Луч 2 попадает на окуляр параллельно главной оптической оси, поэтому он проходит через фокус F'₂. Так как лу­чи 1 и 2 выходят из одной точки В' фокальной плоскости, то после преломления в окуляре они будут параллельны друг другу.

Можно указать главные точки и фокусы микроскопа как еди­ной центрированной оптической системы. Так как луч 1 в про­странстве предметов параллелен главной оптической оси, то он в пространстве изображений пересечет оптическую ось в заднем фо­кусе F'. Главные точки и плоскости найдем из условия, что точка и ее изображение, расположенные в соответствующих главных плоскостях, равноудалены от главной оптической оси.

Чтобы не загромождать чертеж, выберем точку К передней главной плоскости так, чтобы луч, распространяющийся от этой точки параллельно оптической оси, в пространстве предметов сов­падал с лучом 1. Сопряженную ей точку К', расположенную в за­дней фокальной плоскости, найдем из условия, что она лежит на луче 1 и удалена на такое же расстояние от главной оптической оси, как и точка К. Проецируя К' на главную оптическую ось, по­лучаем заднюю главную точку Н'.

Для нахождения передней главной точки из К' направим луч 3 параллельно главной оптической оси. Он пройдет через F₂ до пе­ресечения с задней главной плоскостью объектива. Чтобы опре­делить направление этого луча после выхода из передней глав­ной плоскости объектива, сделаем дополнительное построение: из

 

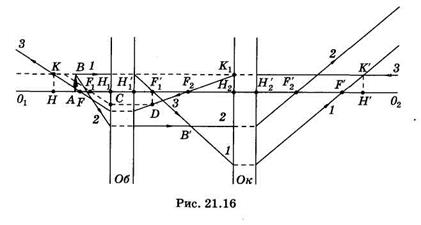
точки D, лежащей в фокальной плоскости, проводим луч DC па­раллельно главной оптической оси, он должен пройти через фокус F1 а луч 3 пройдет параллельно CF_V Пересечение луча 3 с глав­ной оптической осью дает передний фокус F микроскопа, а с лу­чом 1 — положение точки К, которая лежит в передней главной плоскости; Н — передняя главная точка микроскопа.

Отметим, что в этом случае фокусы расположены между глав­ными точками.

Так как показатели преломления среды пространств предмета и изображения одинаковы, то на основании (21.6) фокусные рас­стояния равны между собой: / = —f.

Определим фокусное расстояние микроскопа.

Из подобия 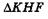и 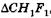, а также 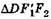и 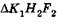соответственно имеем

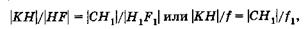(21.12)

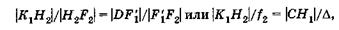(21.13)

где f₁ — фокусное расстояние объектива, f₂ — фокусное расстоя­ние окуляра, — расстояние между задним фокусом объектива и передним фокусом окуляра, называемое оптической длиной тубуса. Разделив (21.12) на (21.13) и учитывая, что \КН\ = \К_гН₂\, имеем f₂: f = 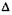: f1 откуда фокусное расстояние микроскопа

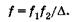(21.14)

Так как и для микроскопа в принципе справедлива общая фор­мула (21.11), то [см. (21.14)]

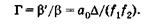(21.15)

Итак, увеличение микроскопа равно отношению произведения оптической длины тубуса на расстояние наилучшего зрения а₀ к произведению f_lf₂ фокусных расстояний объектива и окуляра. Формулу (21.15) можно представить как произведение двух

сомножителей:

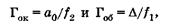(21.16)

где Г_ок — увеличение окуляра, Г_об — увеличение объектива¹.

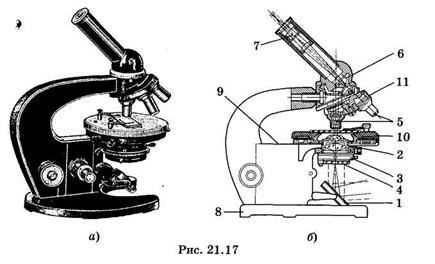
На рис. 21.17 изображены общий вид (а) и схема (б) биологиче­ского микроскопа. Его главные части: основание 8, коробка с мик­рометрическим механизмом 9, предметный столик 10, револь­вер 11с объективами 5, конденсор 2 и окуляр 7. Оптическая сис­тема состоит из двух частей: осветительной и наблюдательной. В осветительную часть входят зеркало 1, конденсор с ирисовой апертурной диафрагмой 3 и съемный светофильтр 4, а в наблюда­тельную — объектив, призма 6 и окуляр, соединенные в тубусе микроскопа.

Пучок лучей от источника света падает на зеркало, которое от­ражает его к диафрагме, проходит через конденсор и исследуе­мый препарат и затем попадает в объектив.

 

 

§ 21.8. Разрешающая способность и полезное увеличение микроскопа. Понятие о теории Аббе

Из формулы (21.15) можно сделать вывод, что при надлежа­щем выборе f1 и f₂ увеличение микроскопа будет сколь угодно большим. Однако на практике биологи, врачи и другие спе­циалисты, работающие с микроскопами, редко используют уве­личения, превышающие 1500—2000. Чтобы уяснить причины такого положения, ознакомимся с понятиями «предел разреше­ния», «разрешающая способность» и «полезное увеличение мик­роскопа».