Правило параллелограмма (четвертая аксиома)
Четвертая аксиома служит основой для сложения сил. Равнодействующая двух сил, приложенных к одной точке, приложена в этой точке и изображается по величине и направлению диагональю параллелограмма, построенного на данных силах. Так, равнодействующей двух сил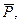 
и 
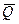, приложенных в точке А (рис. 4, а), будет сила 
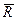, представляющая диагональ параллелограмма ACDB, построенного на векторах заданных сил. Определение равнодействующей двух сил по правилу параллелограмма называется векторным, или геометрическим, сложением и выражается векторным равенством
= 
+ .
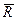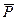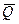При графическом определении равнодействующей двух сил вместо правила параллелограмма можно пользоваться правилом треугольника.
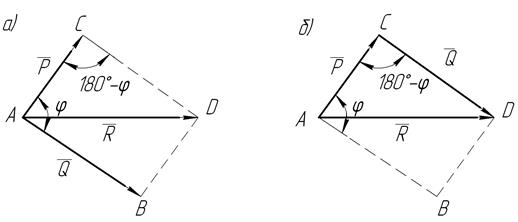
Рис. 4.Сложение двух сил.
Из произвольной точки А (рис. 4, б) проводим, сохраняя масштаб и заданное направление, вектор первой составляющей силы 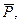из его конца проводим вектор, параллельный и равный второй составляющей силе 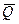. Замыкающая сторона AD треугольника и будет искомой равнодействующей 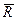. Ее можно также представить как диагональ параллелограмма ABDC, построенного на заданных силах.
1.7. Связи и их реакции
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении. В качестве примера свободного тела приведем летящий воздушный шар или ракету в космосе. Твердое тело называется несвободным, если его перемещение в пространстве ограничено какими-либо другими телами. Все тела, которые так или иначе ограничивают перемещение данного тела, называются его связями. Например, стул, стоящий на полу— несвободное тело; перемещение стула ограничивается полом, для стула пол является связью. Движение висящего на нити шара ограничивается нитью; следовательно, для шара связью служит нить.
В природе нет абсолютного покоя, и тела, стремясь под действием внешних сил перемещаться в пространстве, сами действуют на препятствующие этому перемещению связи. Например, стул, находясь под действием силы тяжести, давит на пол, а шар, висящий на нити, натягивает нить. Одновременно с возникновением действия тела на связь возникает равная по модулю, но направленная в противоположную сторону сила противодействия связи, приложенная к телу. Действие связи на тело называется силой реакции связи или реакцией связи [от латинского «re...» (против) + «actio» (действие), т. е. ответ на внешнее действие].
Таким образом, на несвободное тело действуют две группы внешних сил: заданные силы и реакции связей. К заданным относятся все силы, кроме реакций связей. Чаще всего заданные силы являются активными, т. е. силами, которые могут вызвать движения тел, например сила тяжести, сила тяги, сила электрического взаимодействия и т. д.
При решении задач статики активные силы, как правило, бывают наперед заданными, а реакции связей неизвестны и их требуется определить. Задача определения реакций связей — одна из основных задач статики. Определяя реакции связей, необходимо иметь в виду, что они приложены к телу в точках соприкосновения тела со связью и направлены в сторону, противоположную той, куда связь не дает перемещаться телу. Направление реакции связи зависит от вида связи, ее расположения относительно тела и характера соприкосновения или соединения связи с телом. Для определения реакций связей используют прием освобождения от связей, который формулируется следующим образом. Не изменяя равновесия тела или системы тел, каждую связь, наложенную на систему, можно отбросить, заменив её действием реакции отброшенной связи.
Дата добавления: 2015-06-17; просмотров: 3431;