Основная теорема зацепления. Теорема Виллиса.
Основным требованием, предъявляемым передачам – обеспечение заданного закона изменения передаточного отношения.
В большинстве передач передаточное отношение постоянно. Выявим, каким требованиям должны удовлетворять профили зубьев для выполнения этого требования

Через т.А (касания зубьев) проводим нормаль nn к их профилю.
Нормаль пересекает линию центров О1О2 в т.Р.
Соединим т.А с центрами О1 и О2 : 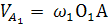 (┴О1А),
(┴О1А),  (┴О2А)
(┴О2А)
Проекции скоростей  и
и  на нормаль должны быть равны – основное условие работоспособности высшей кинем пары.
на нормаль должны быть равны – основное условие работоспособности высшей кинем пары.
Иначе: 1)  => зуб первого колеса будет деформировать зуб второго, 2)
=> зуб первого колеса будет деформировать зуб второго, 2) 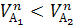 => размыкание зубьев и передачи движения не будет, что не допустимо.
=> размыкание зубьев и передачи движения не будет, что не допустимо.
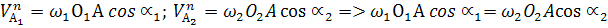
Опустим на нормаль nn из центров О1 и О2 перпендикуляр: 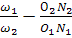 Треугольники О1N1P и О2N2Р – подобные, =>
Треугольники О1N1P и О2N2Р – подобные, => 
Теорема: Нормаль, проведенная через т.касания двух сопряженных профилей должна пересекать линию центров в т.Р и делить межцентровое расстояние О1О2 на отрезки, обратно пропорциональные угловым скоростям. Линия N1N2 – геометрическое место точек контакта сопряжённых профилей и называется – линия зацепления.
В случае постоянства передаточного отношения, контактирующие участки профиля должны быть очерчены по таким кривым, чтобы в любой момент их соприкосновения общей нормали к ним, проведенной бы через 1 и ту же точку Р, называемую полюсом зацепления. Т.е. положение точки Р на линии центров в процессе зацепления остается неизменным. Р = представляет собой мгновенный центр относительного вращения колес. Окружности с центрами О1 и О2 проходящие через полюс – начальные ( 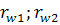 ). В процессе зацепления начальные окружности катятся одна по другой без скольжения. Если радиус одного из зубчатых колес обращается в бесконечность, то зацепление называется реечным. Угол
). В процессе зацепления начальные окружности катятся одна по другой без скольжения. Если радиус одного из зубчатых колес обращается в бесконечность, то зацепление называется реечным. Угол 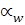 , образованный линией зацепления и общей касательной к начальному отрезку называется углом зацепления. Требование сопряженности обеспечивается, если они являются эвольвентными, циклоидальными и др.
, образованный линией зацепления и общей касательной к начальному отрезку называется углом зацепления. Требование сопряженности обеспечивается, если они являются эвольвентными, циклоидальными и др.
В эвольвентном зацеплении 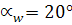
Дата добавления: 2015-06-17; просмотров: 1048;
