Сила давления жидкости на криволинейные поверхности

Нахождение силы давления жидкости на криволинейные поверхности в общем случае сводится к определению трех составляющих суммарной силы и трех моментов относительно осей прямоугольных координат. На практике чаще всего применяются объекты с цилиндрическими поверхностями (резервуары, цилиндрические затворы, стенки круглых труб и т. д.), которые относятся к частному случаю криволинейных поверхностей. Поэтому определим силу давления жидкости на цилиндрическую поверхность (рис. 3.15). Над цилиндрической поверхностью находится жидкость, на свободную поверхность которой действует атмосферное давление. На цилиндрической поверхности выделим крышку площадью S, также выделим объем жидкости V, находящийся над крышкой. На крышке выделим элементарную площадку dS , расположенную на глубине h (рис. 3.15, а). Над этой площадкой выделим элементарный объем dV. Поскольку площадка dS элементарная, то ее можно рассматривать как плоскую. Тогда элементарная сила гидростатического давления dF будет направлена по нормали к элементарной площадке dS и равна:

. (3.24)

Разложим силу dF на горизонтальную dF_Г и вертикальную dF_В составляющие. Горизонтальную составляющую dF_Г можно определить следующим образом:

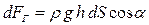. (3.25)

Произведение 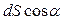является площадью проекции площадки dS на вертикальную грань объема dV, т. е.

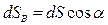. (3.26)

Тогда

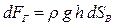. (3.27)

Для нахождения горизонтальной составляющей силы давления на крышку площадью S проинтегрируем уравнение (3.27) по площади проекции крышки S_B на вертикальную грань объема V:

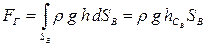, (3.28)

где 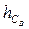– глубина погружения центра масс (точка С_В) вертикальной проекции крышки.

Сила F_Г приложена в центре давления вертикальной проекции крышки (т. D_В на рис. 3.15, б).

Аналогично, вертикальнаясоставляющая dF_В элементарной силы dF будет равна:

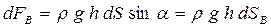, (3.29)

где dS_Г – площадь проекции площадки dS на горизонтальную грань объема dV .

Проинтегрируем уравнение (3.29) и получим вертикальную составляющую силы давления:

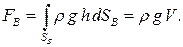(3.30)

Сила F_В приложена в центре масс объема V.

Для цилиндрической поверхности силы F_Г и F_В будут находиться в одной плоскости. Тогда равнодействующая сила гидростатического давления будет равна:

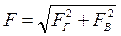. (3.31)

В некоторых случаях жидкость находится под цилиндрической поверхностью (рис. 3.16). Проведя аналогичные рассуждения и выводы, получим формулы для расчета сил F_Г и F_В, аналогичные (3.28) и (3.30), но направление данных сил при этом будет противоположным.