Удар шаров. (Лабораторная работа 8)
Приборы и принадлежности: прибор для исследования столкновения шаров FPM-08 или ФМ-17, линейка.
Теория метода и описание прибора
В настоящей работе рассматривается упругий удар шаров, подвешенных в виде маятников, причем один шар до удара покоится (  ). Удар происходит в положении, соответствующем равновесию тел, и является центральным и прямым. Применяем к ударяющимся шарам закон сохранения импульса для упругого удара
). Удар происходит в положении, соответствующем равновесию тел, и является центральным и прямым. Применяем к ударяющимся шарам закон сохранения импульса для упругого удара
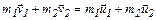 . (4.12)
. (4.12)
Для шаров одинаковой массы в проекциях на горизонтальное направление 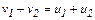 . На основании закона сохранения энергии можно записать:
. На основании закона сохранения энергии можно записать:
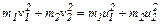 . (4.13)
. (4.13)
Учитывая равенство масс соударяющихся шаров, уравнение (4.13) можно записать в виде
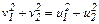 .
.
Решая совместно (4.12) и (4.13) с учетом равенства масс, получим:

 или
или 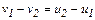 .
.
При упругом ударе часть кинетической энергии шаров переходит в энергию остаточной деформации, тогда
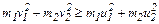 .
.
В этом случае для относительных скоростей получим следующее соотношение:
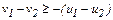 .
.
Относительная скорость изменит направление на противоположное, уменьшаясь по абсолютной величине. Для количественной оценки уменьшения относительной скорости вводится коэффициент восстановления скорости
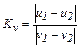 , в нашей работе
, в нашей работе 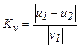 . (4.14)
. (4.14)
В условиях опыта Kv может считаться величиной, зависящей только от материала соударяющихся тел. Коэффициент восстановления скорости служит для характеристики упругих свойств различных материалов и может принимать значения от 0 до 1. Для реальных тел Kv <1.
Не абсолютно упругий удар сопровождается остаточной деформацией. Энергию остаточной деформации можно определить из закона сохранения энергии, для одинаковых шаров получим следующее выражение:
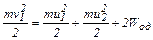 . (4.15)
. (4.15)
Коэффициент восстановления энергии определяется как отношение суммарной кинетической энергии тел после удара к суммарной кинетической энергии тел до удара
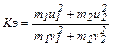 , в нашей работе
, в нашей работе 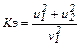 . (4.16)
. (4.16)
Шар, отведенный от положения равновесия на угол α (рис. 4.2), об-
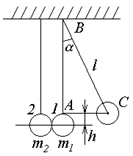 Рис.4.2
Рис.4.2
| ладает запасом потенциальной энергии П = m1gh. Эта энергия в начальный момент удара полностью переходит в кинетическую энергию  , откуда , откуда 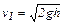 . Из ∆АВС следует . Из ∆АВС следует  , , 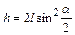 . Подставив h в уравнение для v1, получим . Подставив h в уравнение для v1, получим
|
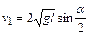 . (4.17)
. (4.17)
До столкновения импульс шаров определяется по формуле
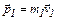 . (4.18)
. (4.18)
После упругого столкновения
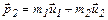 . (4.19)
. (4.19)
где 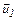 – скорость первого шара после удара,
– скорость первого шара после удара, 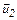 – скорость второго шара после удара.
– скорость второго шара после удара.
Скорости u1 и u2 находим по формулам:
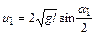 , (4.20)
, (4.20)
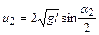 , (4.21)
, (4.21)
где α1 и α2 – угловое расстояние, на которое после удара переместились первый и второй шары.
Дата добавления: 2015-06-17; просмотров: 1296;
