РАБОТА 6. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

Цель работы - исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс крестовины.

Теоретические основы лабораторной работы

При выводе расчётных формул лабораторной работы использованы законы динамики поступательного и вращательного движения твердого тела.

Второй закон Ньютона для поступательного движения тела (m = const)

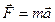(6.1)

где 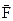- сумма всех внешних сил, приложенных к телу; m – масса тела; 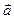- линейное ускорение.

Основной закон динамики вращательного движения твердого тела

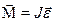(6.2)

где 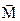- суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; 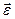- угловое ускорение.

Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.

Момент инерции сплошного твёрдого тела определяется по формуле

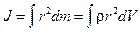где 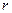- расстояние от элемента объема 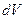с массой dm до оси вращения; r - плотность вещества.

Момент силы относительно точки О это вектор, определяемый как векторное произведение радиус-вектора и силы

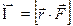
где 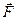- сила, 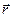- радиус-вектор, проведенный из точки О, в точку приложения силы.

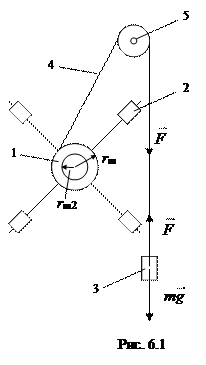
Момент силы относительно оси вращения это проекция вектора момента силы относительно точки 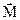на произвольную ось z, которая проходит через точку О:

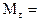
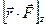Основным элементом маятника Обербека (рис. 6.1) является крестовина (1), на стержнях которой размещены грузы (2). Грузы можно перемещать по стержням и закреплять в нужном положении. Крестовина с грузами насажена на вал, с двумя шкивами различных радиусов (r_ш). На один из шкивов наматывается нить (4), переброшенная через блок (5). К концу нити подвешен груз массой m (3). Под действием силы тяжести груза система приводится в движение.

На вертикальном штативе установлены две неподвижные рамки с оптическими осями (световые барьеры), между которыми может двигаться груз. Груз удерживается в верхнем положении электромагнитом. Время падения груза от верхнего до нижнего светового барьера фиксируется на секундомере.

На груз действует сила тяжести 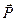= m 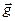и сила натяжения 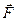. В соответствии со вторым законом Ньютона можно записать

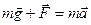
В проекциях на вертикаль (с учётом знаков проекций)

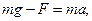(6.3)

где g - ускорение свободного падения; а – величина линейного ускорения, с которым движется груз.

Крестовина приходит во вращательное движение под действием момента силы натяжения

М = Fr_о (6.4)

где r_о - радиус шкива.

Из уравнений (2) - (4) можно получить

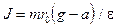
Используя соотношение между угловым и линейным ускорением а e = а/r_0, получим выражение для момента инерции

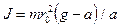(6.5)

Из кинематики известно, что линейное ускорение при равноускоренном движении определяется по формуле

а = 2h/t² (6.6)

где h - путь, пройденный грузом за время t принулевой начальной скорости.

Таким образом, подставляя (6.6) в (6.5), получим расчётную формулу для момента инерции крестовины с грузами

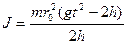(6.7)

Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой 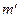(если считать грузы материальными точками), можно выразить формулой

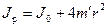(6.8)

где J₀ - момент инерции тела при r = 0.

Из формулы (6.8) следует, что J_р = f(r²). Следовательно, если построить график этой функции в координатах J_р - r², то должна получиться прямая, продолжение которой будет пересекать ось ординат в некоторой точке, соответствующей J_о. Такое построение можно было бы сделать приближенно, «на глаз». Однако математические методы обработки результатов наблюдения позволяют сделать такое построение достаточно точным. Наиболее просто это можно сделать, с помощью метода наименьших квадратов, вычислив J₀ и .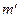

Для этого перепишем формулу (7.8) в виде

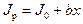, (6.9)

где r² = х и 4m' = b.

Метод наименьших квадратов позволяет найти коэффициенты уравнения (6.9) J₀ и b, используя формулы

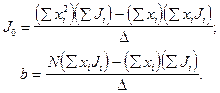(6.10)

здесь 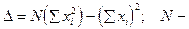число опытов; J_i - экспериментальные значения момента инерции J_э, полученные для каждого опыта.

Порядок выполнения работы

1. Установить на вертикальном штативе со шкалой две неподвижные рамки (световые барьеры) на расстоянии 40-50 см друг от друга.

2. Измерить радиус шкива r_ш, на котором ведется эксперимент и путь, пройденный грузом.

3. Установить грузы на стержнях на максимальное расстояние от оси вращения и закрепить.

4. Включить установку нажатием кнопки «сеть».

5. Отключить электромагнит нажатием кнопки «пуск» и «сброс».

6. Выбрать необходимый груз по указанию преподавателя (табл.6.1).

Таблица 6.1

Основной груз	m = 53 г. или m = 100 г.

Перегрузы:	m₁ = 1,554 г.	m₆ = 2,504 г.	m₁₀ = 19,528 г.
m₂ = 1,705 г.	m₇ = 2,714 г.	m₁₁ = 26,258 г.
m₃ = 1,829 г.	m₈ = 2,948 г.	m₁₂ = 32,836 г.
m₄ = 2,055 г.	m₉ = 12,800 г.	m₁₃ = 39,251 г.
m₅ = 2,206 г.

7. Намотать нить на шкив, установив подвешенный груз на уровне верхней рамки (над оптической осью верхнего светового барьера).

8. Закрепить груз, нажав кнопку «пуск» и обнулить счетчик (кнопка «сброс»).

9. Отпустить груз (кнопка «пуск») записать измеренное время движения груза t до оптической оси нижней рамки.

10. Произвести не менее 3-х измерений времени t и вычислить .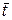

11. Сместить грузы на стержнях на 1 – 2 деления к центру и повторить п.п. (3÷6), измеряя расстояние r от оси вращения до центра масс груза.

12. Повторить измерения для 8 – 10 положений грузов.

13. Записать результаты эксперимента в таблицу 6.2.

Таблица 6.2

Физ. величина	r	t	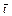J_э	J_р
Ед. измерения Номер опыта


…
n

<1 2 345 6 7 >

Дата добавления: 2015-06-17; просмотров: 2424;